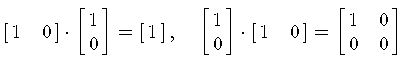Invertierbare Matrizen

Es sei daran erinnert:

Sei R ein Ring. Ein Element r in R heißt invertierbar, wenn es ein Element r' in R mit rr' = 1 = r'r gibt, und man schreibt dann r' = r^-1.
Ist R nicht kommutativ, und sind a,b in R mit b invertierbar, so darf man statt ab^-1 nicht einfach einen Bruch schreiben: denn im allgemeinen wird gelten ab^-1 ≠ b^-1a, aber der Schreibweise

kann man ja nicht ansehen, ob es sich um die Reihenfolge ab^-1 oder b^-1a handeln soll!

Die Menge der invertierbaren Elemente eines Rings bildet (bezüglich der Multiplikation) eine Gruppe.

Beweis: Es ist nur zu zeigen, dass gilt: sind r, s in R invertierbare Elemente, so ist auch rs invertierbar. Aber man kann das Inverse zu rs einfach hinschreiben, nämlich s^-1r^-1. Natürlich braucht man auch, dass des Inverse eines invertierbaren Elements selbst wieder invertierbar ist...

---

Ist R ein Ring, so ist auch M(n×n,R) ein Ring. Die Definition besagt also in diesem Fall: Eine (n×n)-Matrix A mit Koeffizienten in R ist invertierbar, wenn es eine (n×n)-Matrix A' mit Koeffizienten in R gibt mit AA' = I = A'A (dabei ist I = I_n die (n×n)-Einheits-Matrix.

Man schreibt GL(n,R) für die Gruppe der invertierbaren (n×n)-Matrizen, (GL steht für "general linear group"). Für n = 1 ist dies nichts anderes als die Gruppe der invertierbaren Elemente von R.

Für n > 1 (und R ≠ 0) ist GL(n,R) nicht kommutativ. Denn E₁₂ und P₁₂ gehören zu GL(n,R), und es ist Q₁₂(1)P₁₂ ≠ P₁₂Q₁₂(1).

---

---

Und es sei erinnert an:

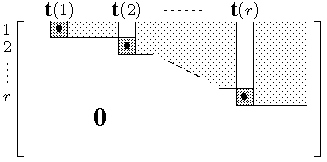
Satz 1': Durch elementare Zeilen-Umformungen der ersten Art kann jede Matrix mit Koeffizienten in einem Körper in Zeilenstufenform gebracht werden, wobei zusätzlich gilt: in den Pivot-Spalten ist nur noch der Pivot-Koeffizient von Null verschieden.

Beweis:
(1) impliziert (2): Trivial.
(2) impliziert (3): Aus vA = 0 folgt v = vI = vAB = 0.
(3) impliziert (4): Sei P ein Produkt von Elementar-Matrizen, sodass PA in Zeilenstufenform ist und in den Pivot-Spalten nur der Pivot-Koeffizient von Null verschieden ist (hier verwenden wir Satz 1'). Sei r die Anzahl der Pivot-Positionen. Wir behaupten: r = n. Ist r < n, gilt für die (1×n)-Matrix w = [0,...,0,1] wPA = 0. Also gilt wegen (3): wP = 0. Da P invertierbar ist, gilt w = wI = wPP^-1 = 0P^-1 = 0, Widerspruch.

Wegen r = n sind alle Spalten Pivot-Spalten und demnach ist D = PA eine Diagonalmatrix, und alle Diagonalkoeffizienten sind von Null verschieden. Also ist D invertierbare Diagonalmatrix und es ist A = P^-1D. Mit P ist auch P^-1 Produkt von Elementar-Matrizen.

(4) impliziert (5): trivial.
(5) impliziert (1). Elementarmatrizen sind invertierbar, Produkte invertierbarer Matrizen sind invertierbar.

Die Äquivalenz von (1) mit den drei letzten Aussagen (6) (7), (8) ergibt sich dadurch, dass man statt mit Zeilen-Operationen mit Spalten-Operationen arbeitet.
(Oder auch dadurch, dass man die Äquivalenz von (1) mit (2), (3), (4) auf die zu A transponierte Matrix ^tA anwendet).

Man beachte, dass in der angegebenen Reihenfolge nur eine Implikation nicht offensichtlich ist, nämlich: (3) impliziert (4); für diese Implikation verweist man auf Satz 1, also auf die Gauss-Elimination.

Zusatz: Diese Charakterisierung der invertierbaren Matrizen und ihr Beweis liefern ein effektives Verfahren, um das Inverse einer invertierbaren Matrix A zu berechnen, und um eine invertierbare Matrix A als Produkt von Elementarmatrizen und einer invertierbaren Diagonalmatrix zu schreiben. Nämlich: Suche mit Hilfe der Gauss-Elimination Elementarmatrizen E1,...,Es (oder auch Permutationsmatrizen), sodass D = Es...E1A eine Diagonalmatrix ist. Dann gilt A-1 = D-1Es...E1. A = E1-1...Es-1D. Beachte: Das Inverse einer Elementarmatrix ist wieder eine Elementarmatrix! Dabei braucht man nicht zu wissen, ob die gegebene Matrix A invertierbar ist: Die Gauss-Elimination ist immer anwendbar und es gilt: Genau dann ist A invertierbar, wenn die Gauss-Elimination eine invertierbare Diagonalmatrix liefert.

Beweis: (D^-1E_s...E₁)A = D^-1(E_s...E₁A) = D^-1D = I. Es gilt also die Bedingung (6) für B = D^-1E_s...E₁.

Die zweite Formel folgt durch Invertieren.

• Die induktive Suche nach derartigen Elementarmatrizen wird gerade durch das Gauss'sche Eliminationsverfahren geleistet.
• Das Invertieren von Elementarmatrizen ist unproblematisch: Es ist E_ij(λ)^-1 = E_ij(-λ).

Beispiel für das effektive Durchführen dieses Verfahrens: siehe Fischer, 2.7.5.

Beweis: Die erste Aussage folgt unmittelbar aus den Charakterisierungen (3) und (7).
Die zweite Aussage folgt unmittelbar aus der ersten.
Die dritte Aussage folgt aus dem obigen Verfahren zum Invertieren von Matrizen.

Warnung, zur Implikation: (2) impliziert (1): Für beliebige (nicht notwendig quadratische) Matrizen folgt aus AB = I nicht, dass auch BA = I gilt
(wir schreiben hier I für zwei möglicherweise ganz verschiedene Matrizen - beides sind Einheits-Matrizen, können aber verschiedene Größen haben).
Hier ist ein Beispiel:

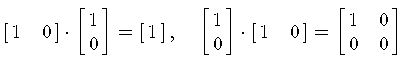
Im Gegenteil! Wir werden später zeigen: Ist A eine (m×n)-Matrix, B eine (n×m)-Matrix mit AB = I, und ist m ≠ n, so ist BA ≠ I.

• Permutationsmatrizen,
• invertierbare obere Dreiecksmatrizen,
• invertierbare untere Dreiecksmatrizen,
  und man spezialisiert weiter:
  • obere Dreiecksmatrizen, deren Diagonal-Koeffizienten alle gleich 1 sind, und entsprechend:
  • untere Dreiecksmatrizen, deren Diagonal-Koeffizienten alle gleich 1 sind,
  • invertierbare Diagonalmatrizen (dies sind gleichzeitig obere und untere Dreiecksmatrizen)

  Jede invertierbare obere Dreiecksmatrix A kann man (eindeutig!) als Produkt A = DA' = A"D schreiben, wobei D eine invertierbare Diagonalmatrix ist und A', A" obere Dreiecksmatrizen sind, deren Diagonal-Koeffizienten alle gleich 1 sind.
  Entsprechend gilt: Jede invertierbare untere Dreiecksmatrix ...

Eine systematische Beschreibung des Aufbaus einer beliebigen Matrix mit Hilfe einer Permutationsmatrix und zweier Dreiecksmatrizen liefern die folgenden Ergebnisse:

Leider werden sie in den meisten Anfänger-Büchern nur am Rand erwähnt, eine schöne Darstellung findet man im Buch von Brieskorn!

Satz (LR-Zerlegung). Sei K ein Körper. Jede Matrix A in GL(n,K) kann in der Form A = PLR geschrieben werden, wobei P eine Permutationsmatrix, L eine untere Dreeicksmatrix, R eine obere Dreiecksmatrix ist. (Dabei kann man zusätzlich annehmen, dass die Diagonalkoeffizienten von L (oder von R) alle gleich 1 sind.)

Die LR-Zerlegung einer quadratischen Matrix spielt eine wichtige Rolle in der Numerik. Viele effektive Verfahren zum Lösen linearer Gleichugnssysteme arbeiten mit LR-Zerlegungen.

L steht für "links" (oder "left"), R steht für "rechts" (oder "right"); obwohl man nicht "Linksmatrix", sondern "untere Dreiecksmatrix". und nicht "Rechtsmatrix", sondern "obere Dreiecksmatrix" sagt.

Zum Beweis der LR-Zerlegung:
Man mache sich klar, dass wir nur den Beweis von Satz 1 so modifizieren müssen, dass wir zuerst alle notwendigen Permuationen durchführen, und danach erst elementare Zeilenoperationen (der ersten Art, und zwar eben nur solche der Form Q_ij(λ) mit i > j) - dass es also eine Permutationsmatrix P' und ein Produkt L' von Elementarmatrizen der Form Q_ij(λ) mit i > j gibt mit L'P'A = R. Daraus folgt dann A = PLR mit P = P'^-1 und L = L'^-1.

Statt auf Satz 1 zurückzugreifen, werden wir weiter unten die Existenz von LR-Zerlegung aus der Bruhat-Zerlegung ableiten. (FEHLT NOCH!)

Satz (Bruhat-Zerlegung). Sei K ein Körper. Jede Matrix A in GL(n,K) kann in der Form A = R'PR geschrieben werden, wobei P eine Permutationsmatrix, und R, R' invertierbare obere Dreiecksmatrizen sind. (Dabei kann man zusätzlich annehmen, dass die Diagonalkoeffizienten von R' (oder von R) alle gleich 1 sind).

Die Gruppe GL(n,K) ist ein typisches Beispiel einer "algebraischen Gruppe". In der Theorie der "algebraischen Gruppen" spielen Bruhat-Zerlegungen eine wichtige Rolle. Fixiert man eine Permutationsmatrix P und betrachtet man alle Matrizen in GL(n,K) der Form A = R'PR mit oberen Dreiecksmatrizen R, R', so nennt man dies die Bruhat-Zelle zu P.

Beweis. Wir zeigen mit Induktion nach t, dass es invertierbare obere Dreiecksmatrizen R_i und R'_i mit 1 ≤ i ≤ t gibt, so dass die Matrix A_t = R'_t...R'₂R'₁AR₁R₂...R_t die folgenden Eigenschaften hat: es gibt paarweise verschiedene σ(j) mit 1 ≤ j ≤ t und 1 ≤ σ(j) ≤ n mit:
1. Der Koeffizient in der Position (σ(j),j) ist 1.
2. Alle anderen Koeffizienten in den ersten t Spalten sind 0.
3. Alle anderen Koeffizienten in den Zeilen mit Zeilenindex σ(j), mit 1 ≤ j ≤ n, sind 0.
Beweis: Die Aussage sei richtig für ein t < n. Betrachte die Spalte von A_t mit Spaltenindex t+1. Dies kann keine Nullspalte sein, da A_t invertierbar ist. Wähle s maximal, sodass der Koeffizient von A_t an der Position (s,t+1) von Null verschieden ist. Setze σ(t+1) = s. Dann sind die Zahlen σ(j) mit 1 ≤ j ≤ t+1 paarweise verschieden (und liegen zwischen 1 und n).
• Durch Multiplikation mit einer invertierbaren oberen Dreiecksmatrix R_t+1 von rechts können wir erreichen, dass der Koeffizient an der Position (σ(t+1),t+1) zu 1 wird, und dass die Koeffizienten an den Positionen (σ(t+1),j) mit j > t+1 zu 0 werden.
  (Beachte: Danach ist in der Zeile mit Zeilenindex σ(t+1) nur noch der (σ(t+1),t+1)-Koeffizient von Null verschieden).
• Durch Multiplikation mit einer invertierbaren oberen Dreiecksmatrix R'_t+1 von links können wir erreichen, dass die Koeffizienten in den Positionen (i,t+1) mit i < σ(t+1) zu 0 werden.
  (Beachte: Danach ist in der Spalte mit Spaltenindex t+1 nur noch der (σ(t+1),t+1)-Koeffizient von Null verschieden).
• Setze A_t+1 = R'_t+1A_tR_t+1.
Dann erfüllt A_t+1 die gewünschten Bedingungen (entsprechend zu den Bedingungen 1,2,3)

Für t = n sehen wir: P = A_n ist eine Permutations-Matrix. Setzen wir R = (R₁R₂...R_n)^-1 und R' = (R'₁...R'₂R'₁)^-1 so sind dies invertierbare obere Dreiecksmatrizen und es gilt A = R'PR.

Bei der angegebenen Konstruktion sind die Diagonalkoeffizienten von R' gleich 1. Natürlich können wir das Verfahren so modifizieren, dass die Diagonalkoeffizienten von R gleich 1 sind. Damit ist der Beweis abgeschlossen.

Wir wollen jetzt genauer analysieren, welche Gestalt die von uns konstruierte Matrix R' hat.

Es ist R' = (R'_n...R'₂R'₁)^-1, und jede der Matrizen R'_t ist ein Produkt von oberen Dreiecksmatrizen der Form Q_ij(λ):

Die Linksmultiplikation mit Q_ij(λ) addiert das λ-Fache der j-ten Zeile zur i-ten Zeile. Wir wissen daher einiges über das Indexpaar (i,j) :

Da Qij(λ) ein Faktor von einem R't ist, ist also für dieses t j = σ(t), denn im t-ten Schritt haben wir Vielfache der Zeile mit Index σ(t) zu anderen Zeilen addiert. Im t-ten Schritt haben wir Vielfache dieser σ(t)-ten Zeile zu Zeilen addiert, die darüber liegen, also ist i < σ(t). Zusammen mit j = σ(t) liefert dies gerade: i < j, also ist Qij(λ) eine obere Dreiecksmatrix ist (was wir allerdings schon wissen !). Wir haben ein Vielfaches der σ(t)-ten Zeile zur i-ten Zeile addiert, um den Koeffizienten an der Stelle (i,t) zum Verschwinden gebracht. Nach dem (t-1)-ten Schritt sind die Koeffizienten an den Positionen (σ(j),t) mit j < t alle Null, also können wir annehmen, dass i keine der Zahlen σ(1),...,σ(t-1) ist. Und natürlich ist i auch verschieden von σ(t). Das heißt aber: σ-1(i) ist keine der Zahlen 1,2,...,t. Daher gilt: t < σ-1(i). (Anders formuliert: Der Zeilenindex i ist verschieden von σ(1),...,σ(t), demnach liegt die Position (i,σ-1(i)) rechts von (i,t), und daher ist t < σ-1(i).)

Aber (1) (2) und (3) zusammen besagen:

i < j    und    σ-1(j) = t < σ-1(i).

Da das Inverse von Q_ij(λ) gerade Q_ij(-λ) mit gleichem Indexpaar (i,j) ist, sehen wir:

R' ist ein Produkt von Matrizen der Form Qij(λ) mit i < j und σ-1(j) < σ-1(i).

Wir können also R' = B₁...B_m schreiben, wobei die B_s derartige Matrizen der Form Q_ij(λ) sind.

Ist B_s = Q_ij(λ), so setze L_s = Q_τ(i),τ(j)(λ), mit τ = σ^-1. Wichtig ist: Während B_s wegen i < j eine obere Dreiecksmatrix ist, ist L_s eine untere Dreiecksmatrix, denn τ(i) > τ(j).

Es sei daran erinnert, dass P = P(σ) die Permutationsmatrix zur Permutation σ ist, und dass gilt:

B_sP(σ) = Q_ij(λ)P(σ) = P(σ)Q_τ(i),τ(j)(λ) = P(σ)L_s (dies sieht man unmittelbar, wenn man Q_ij(λ) = I + λE_ij schreibt, und sich daran erinnert, wie man Permutationsmatrizen mit Basismatrizen multipliziert).

Insgesamt sehen wir: R'P = PL mit L = L₁...L_m. Denn

R'P(σ) = B₁...B_mP(σ) = B₁...B_m-1P(σ)L_m = ... = P(σ)L₁...L_m = P(σ)L

Als letztes sei bemerkt, dass L als Produkt von unteren Dreiecksmatrizen selbst eine untere Dreiecksmatrix ist!.

Haupt-Satz. Sei K ein Körper. Jede Matrix A in GL(n,K) kann in der Form A = R'PR geschrieben werden, dabei ist R eine invertierbare obere Dreiecksmatrix ist P eine Permutationsmatrix, R' eine obere Dreiecksmatrix mit allen Diagonalelementen gleich 1, sodass zusätzlich gilt: P-1R'P ist eine untere Dreiecksmatrix.

Die Faktorisierung A = R'PR ist eine Bruhat-Zerlegung, und setzen wir L = P-1R'P, so sehen wir, dass gilt: A = PLR, dies ist eine LR-Zerlegung. Wir erhalten also gleichzeitig eine Bruhat-Zerlegung und eine LR-Zerlegung, mit gleichen Matrizen P und R, und die Matrizen R' und L' sind zueinander konjugiert: L = P-1R'P, R' = PLP-1.

Zusatz (ohne Beweis): Ist A gegeben, so sind die Matrizen R, P, R' (und damit auch L = P-1R'P) eindeutig bestimmt!