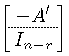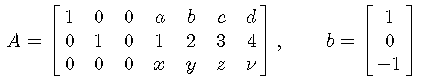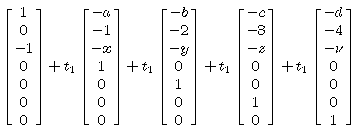|
Das Lösen von linearen Gleichungssystemen |
Sei K ein Körper.
Gegeben seien eine (m×n)-Matrix A und eine
(m×1)-Matrix b mit Koeffizienten in K.
Wir betrachten das lineare Gleichungssystem
dabei bedeutet X die (n×1)-Matrix mit
Koeffizienten X1,...,Xn
(man nennt sie "Unbekannte" oder "Variable").
Gemeint ist folgendes: Gesucht sind "Lösungen
dieses Gleichungssystems", unter der Lösungsmenge
Lös(A,b) versteht man folgendes:
|
Lös(A,b) = { x in M(n×1,K) |
Ax = b } |
(1)
Um alle Lösungen des Gleichungssystems AX = b
zu erhalten, sucht man üblicherweise
- eine Lösung x'
von AX = b und
- alle Lösungen x des homogenen
Gleichungssystems AX = 0.
und man bildet x'+x. Auf diese Weise erhält man alle
Lösungen:
Lös(A,b) = x' + Lös(A,0).
Beachte: Lös(A,0) ist eine Untergruppe von M(n×1,K), die
unter Skalarmultiplikation abgeschlossen ist (ein "Unterraum").
|
Dabei setzen wir: x' + Lös(A,0) = {x'+x | x in Lös(A,0)}.
Weiterführende Bemerkung:
Eines der wichtigsten Themen der Lineare Algebra ist die
Untersuchung von derartigen "Unterräumen", dies
wird bald geschehen.
Beweis: Ist x in Lös(A,0), so ist x+x' in Lös(A,b),
denn A(x+x') = Ax + Ax' = b+0 = b.
Umgekehrt gilt: ist x" in Lös(A,b), so ist x"-x' in
Lös(A,0), denn A(x"-x') = Ax" - Ax = b - b = 0.
Und x" = x' + (x"-x').
(Verwendet wird hier das Distributivgesetz und die Rechenregeln
für die Addition von Matrizen.)
(2)
Ist P in M(m×m,K) invertierbar, so gilt
Lös(A,b) = Lös(PA,Pb).
.
Also kann man zur Bestimmung von Lös(A,b) die Matrix
[A|b] durch eine Matrix [PA|Pb] in Zeilenstufenform
(oder sogar in Schubert-Normalform) ersetzen.
|
Für eine beliebige (m×m)-Matrix P ist
Lös(A,b) eine Teilmenge von Lös(PA,Pb), denn
aus Ax = b folgt PAx = Pb.
(Verwendet wird hier die Assoziativität der
Matrizenmultiplikation.)
Ist nun P invertierbar, so gilt
Lös(A,b) = Lös(P-1PA,b), und
dies ist
eine Teilmenge von Lös(PA,b).
|
(3)
Sei nun [A|b] in Zeilenstufenform. Ist n+1 Pivot-Spalten-Index,
so besitzt AX = b keine Lösung.
(Andernfalls gibt es Lösungen.)
|
Weiterführende Bemerkung:
Wir werden bald zeigen:
Die Pivot-Positionen jeder zu A gehörenden
Zeilenstufenform hängen nur von der Matrix A ab.
Insbesondere nennt man die Anzahl der Pivot-Positionen den
"(Zeilen-)Rang" rang(A) der Matrix A. Offensichtlich ist
der Rang
der Matrix [A|b] entweder gleich rang(A) oder gleich
rang(A)+1. Genau dann ist m+1 Pivot-Spalten-Index der Matrix
[A|b], wenn gilt: rang([A|b]) = rang(A)+1.
Beweis: Es sei n+1 Pivot-Spalten-Index.
Bezeichnen wir mit (1,t(1)),...,(r,t(r)) die Pivot-Positionen
von A, so ist (r+1,n+1) die Pivot-Position in der (n+1)-ten
Spalte. Die (r+1)-te Gleichung lautet dann:
Σj 0.Xj = br+1
und es ist br+1 ≠ 0. Eine deartige Gleichung
besitzt natürlich keine Lösung.
Ist dagegen n+1 kein Pivot-Spalten-Index, so liefern die
folgenden Überlegungen Lösungen!
Um effektiv Lösungen zu berechnen, können wir
voraussetzen,
- dass [A|b] in Schubert-Normalform ist und n+1 kein
Pivot-Spalten-Index ist (siehe (2) und (3)),
zusätzlich auch:
- dass [A|b] keine Null-Zeile besitzt
(denn die Null-Zeilen liefern keine Information über
die Lösungsmenge).
- dass die Pivot-Spalten die ersten Spalten sind
(das Vertauschen von Spalten der Matrix A bedeutet ein
Umbenennen [= Umnummerieren] der Unbekannten.)
Also betrachten wir jetzt eine Matrix A der Form
A = [Ir|A'], dabei ist A' eine (r×(n-r))-Matrix,
und eine (r×1)-Matrix b:

(4)
- Die Lösungsmenge des homogenen Gleichungssystems
[Ir|A']X = 0 sind die Linearkombinationen der
Spalten f(1),...,f(n-r)
der Matrix
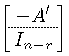
- Der Spaltenvektor
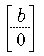 ist eine Lösung des inhomogenen
Gleichungssystems [Ir|A']X = b.
ist eine Lösung des inhomogenen
Gleichungssystems [Ir|A']X = b.
Insgesamt gilt also:
-
Die Lösungen des inhomogenen
Gleichungssystems [Ir|A']X = b sind die
Spalten-Vektoren der Form
 | +Σj=1
n-r λjf(j),
|
mit λj in K.
-
Die Lösungen des homogenen
Gleichungssystems [Ir|A']X = 0 sind die
Spalten-Vektoren der Form
Σj=1
n-r λjf(j),
mit λj in K.
|
Beweis:
Es ist klar, dass
 eine Lösung des
inhomogenen Gleichungssystems ist (nachrechnen!).
eine Lösung des
inhomogenen Gleichungssystems ist (nachrechnen!).
Der Zusatz ("Insgesamt gilt also...") basiert auf der Aussage 1:
Man erhät alle Lösungen eines inhomogenen Systems,
indem man zu einer speziellen Lösung des inhomogenen
Systems alle des homogenen Systems addiert.
Es genügt also, das homogene Gleichungssystem zu betrachten.
Setze
| C = | 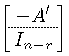 |
Man sieht sofort:
[Ir|A']C = 0, demnach sind die Spalten von
C Lösungen des homogenen Gleichungssystems
[Ir|A']X = 0.
Sei umgekehrt x eine Lösung des homogenen Gleichungssystems
[Ir|A']X = 0. Wir zeigen:
x = Σj=1n-r xr+j-1f(j).
Um dies zu zeigen, betrachten wir den Vektor
y = x -
Σj=1n-r xr+jf(j).
Offensichtlich sind die letzten n-r Koeffizienten von y gleich 0.
Und natürlich ist y als Linearkombination der Vektoren
y, f(1),...,f(n-r) ein Lösungsvektor.
Es genügt zu zeigen: Der einzige Lösungsvektor
des Gleichungssystems [Ir|A']X = 0, dessen letzte
n-r Koeffizienten gleich 0 sind, ist der Nullvektor. (Denn dann
gilt y = 0, also die behauptete Gleichheit).
Aber multiplizieren wir für 1 ≤ i ≤ r
die i-te Zeile von A mit y, so erhalten wir gerade den
Koeffizienten yi. Dies zeigt: yi = 0.
Also y = 0.
Weiterführende Bemerkungen:
- Die Spalten f(1),...,f(n-r) sind "linear unabhängig"
, sie bilden also eine "Basis" von
Lös([Ir|A'],0). Dies wird später gezeigt.
- Wir werden später das Lösen von
linearen Gleichungssystemen in der Sprache der "linearen
Abbildungen" formulieren: gesucht ist das Urbild eines
Vektors unter einer linearen Abbildung
g : Kn → Km.
Und wir werden all dies auch in der Sprache der "affinen
Geometrie" umformulieren.
- Und wir werden zumindest die Lösungsformel für
homogene lineare Gleichungssysteme als Aussagen einer
"Dualitätstheorie" interpretieren.
Beispiel
Hier als Beispiel das Gleichungssystem AX = b
mit
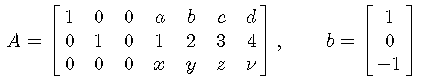
(dabei haben wir als Koeffizienten neben rationalen Zahlen
auch einige Variable, nämlich a,b,c,d,x,y,z,ν, verwendet).
Maple liefert die Lösungen in folgender Form:
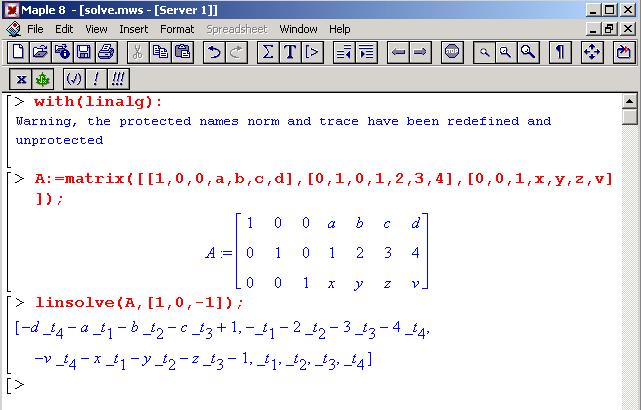
Im Rahmen der Vorlesung schreiben wir derartige Elemente in
der Form:
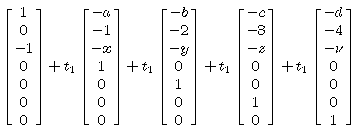
Links sieht man eine spezielle Lösung des
gegebenen (inhomogenen) Gleichungssystems. Die
Linearkombinationen der vier Vektoren mit den Faktoren
t1, t2, t3, t4
stellen
die Lösungen des zugehörigen homogenen
Gleichungssystems AX = 0 dar.
Diese Beschreibung der Lösungsmenge entspricht gerade
derjenigen im ersten Kasten (1).
BIREP
Last modified: Sun Nov 7 10:28:35 CET 2004