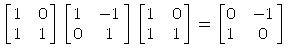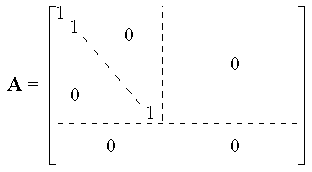Basis-Matrizen: Wir bezeichnen mit E_ij die Matrix, mit (i,j)-Koeffizient gleich 1, während alle anderen Koeffizienten gleich 0 sind.
(Eigentlich müsste man auch noch hinschreiben, dass es sich hierbei um eine (m×n)-Matrix handelt, man meist verzichtet man darauf. Es gibt also in jeder Menge M(m×n,R) genau mn Basis-Matrizen.)

Dabei verwendet man die folgende Rechenregel für das Muliplizieren von Basis-Matrizen:


EijEst =		Eit	falls	j=s
		0		j≠s

Insbesondere gilt für quadratische Matrizen: Eij2 = Eii   falls i=j 0 i≠j Die Basisvektoren Eii sind also idempotent, die Basisvektoren Eij mit i≠j sind nilpotent.

Die Rechenregel für das Multiplizieren von Basis-Matrizen besitzt folgende Verallgemeinerung:
Ist A eine Matrix und ist das Produkt E_ijA definiert, so entsteht E_ijA aus A auf folgende Weise:

• Die i-te Zeile von E_ijA ist die j-te Zeile von A
• Alle anderen Zeilen von E_ijA sind Null-Zeilen.

Jede Matrix A lässt sich (eindeutig!) als Linearkombination der Basis-Matrizen E_ij schreiben:

A = (aij)ij = Σij aijEij.

• Elementare Zeilen-Umformungen einer Matrix A:
  1. Multiplikation von links mit einer Matrix der Form I+λE_ij mit i≠j.
     Die Matrix (I+λE_ij)A entsteht aus A, indem zur i-ten Zeile von A das λ-fache der j-ten Zeile von A addiert wird.
  2. Vertauschung zweier Zeilen (sie ergibt sich durch Multiplikation von links mit einer geeigneten "Permutationsmatrix").

Satz 1: Durch elementare Zeilen-Umformungen kann jede Matrix mit Koeffizienten in einem Körper in Zeilenstufenform gebracht werden.
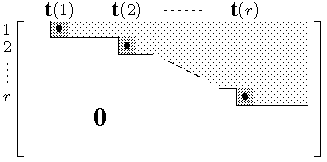
Dabei nennt man eine (m×n)-Matrix eine Zeilenstufenform (oder: Treppennormalform), falls es Zahlen 1 ≤ t(1) < ... < t(r) ≤ n    gibt mit Es ist ai,t(i) ≠ 0 für alle 1 ≤ i ≤ r. Ist aij ≠ 0, so ist i ≤ r und j ≥ t(i). Man nennt die Paare (i,t(i)) die Pivot-Positionen.	Die fetten Punkte markieren die Pivot-Positionen.

Beweis des Satzes, gleichzeitig eine praktische Anleitung zur Durchführung:

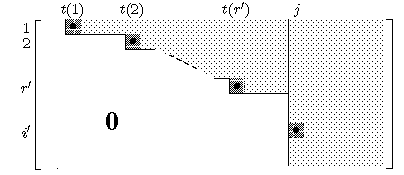
Induktives Verfahren: Die ersten j-1 Spalten seien schon in Zeilenstufenform, mit den Pivot-Positionen (1,t(1)),...,(i',t(r')). Fall 1: Ist ai,j = 0 für alle i > r', so sind die ersten j Spalten in Zeilenstufenform. Fall 2: Andernfalls gibt es ein i' > r' mit ai',j ≠ 0. Vertausche die i'-te Zeile mit der (r'+1)-ten Zeile, man erhalte auf diese Weise eine Matrix B = (bij)ij. Es ist br'+1,j ≠ 0. Addiere zu den Zeilen mit Index i > r'+1 ein Vielfaches der (r'+1)ten Zeile, und zwar mit dem Faktor -bi,j/br'+1,j. 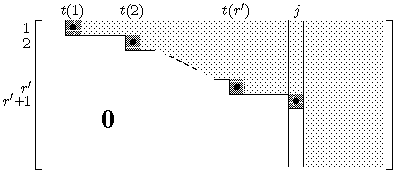Nun sind die ersten j Spalten in Zeilenstufenform.

Man nennt dieses Verfahren

• Gauss'sche Elimination
  (nach Gauss (1777-1855) - Gauss selbst nannte dieses Verfahren. eliminatio vulgaris).
• In China ist das Verfahren mindestens seit den Neun Büchern ... (200 v.u.Z.) bekannt und wird Fang-Cheng-Algorithmus genannt.
  

  fang cheng:

  Rechtecks-Muster, Gleichungen

• Auf diese Weise kann man jedes vorgegebene Gleichungssystem numerisch lösen - im Prinzip, so wie jemand im Prinzip Klavierspielen kann, der weiß welche Taste für welche Note angeschlagen werden muss. In Wirklichkeit sind mit dernmerischen Lösung von großen Gleichungssystemen, wie sie in den Anwendungen vorkommen, schwierige Probleme verbunden. Es gibt eine ausgedehnte Litertur über dieses Gebiet (die numerische Lineare Algebra ) und ständig erscheinen neue Forschungsarbeiten! (nach Jänich, p.175).

• Das Verfahren ist in allen Computer-Algebra-Systemen implementiert. In MAPLE verwendet man die Befehle:
  1. addrow(A,i,j,x) um das x-Fache der i-ten Zeile zur j-ten Zeile zu addieren
  2. swaprow(A,i,j) um die i-te und die j-te Zeile zu vertauschen.
  Und man braucht dies nicht in Einzelschritten zu tun:
  • gausselim(A) liefert sofort das Ergebnis.

• Wir verwenden nur elementare Zeilenumformungen der ersten Art (also das Addieren eines Vielfachen der j-ten Zeile zur i-ten Zeile, mit i≠j).
• Als Ergebnis verlangen wir, dass in den Pivot-Spalten nur noch der Pivot-Koeffizient von Null verschieden ist.

Satz 1': Durch elementare Zeilen-Umformungen der ersten Art kann jede Matrix mit Koeffizienten in einem Körper in Zeilenstufenform gebracht werden, wobei zusätzlich gilt: in den Pivot-Spalten ist nur noch der Pivot-Koeffizient von Null verschieden.

Beweis: 1. Das Vertauschen zweier Zeilen mit anschließender Multiplikation einer dieser Zeilen mit -1 kann als durch elementare Zeilenumformungen der ersten Art erzielt werden: Es gilt: die Matrix Q_ji(1)Q_ij(-1)Q_ji(1)A entsteht aus der Matrix A durch Vertauschung der i-ten und der j-ten Zeile und Multiplikation der neuen i-ten Zeile mit -1.
Der Fall der (2×2)-Matrizen Q_ji(1), Q_ij(-1) mit i=1, j=2 zeigt, was pasiert:

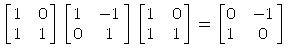
2. Addiert man (in jedem Schritt) zu allen Zeilen mit Index i ≠ r'+1 ein Vielfaches der (r'+1)ten Zeile, und zwar mit dem Faktor -b_i,j/b_r'+1,j, so erhält man induktiv eine Matrix, in der in den Pivotspalten nur der Pivot-Koeffizient von Null verschieden ist.

Insgesamt verwenden wir zum Ändern nur invertierbare Matrizen:

• Die Elementarmatrizen sind invertierbar: (I+λE_ij)(I-λE_ij) = I.
• Sei D(d₁,...,d_n) die (n×n)-Diagonalmatrix mit (i,i)-Koeffizient d_i, also gleich Σ_i d_iE_ii, und sind alle d_i im Grundring R invertierbar, so ist D(d₁,...,d_n) D(d₁^-1,...,d_n^-1) = I

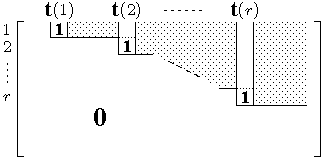
Wir nennen eine Zeilenstufenform eine Schubert-Normalform (oder auch: Gauss-Jordan-Form) falls zusätzlich gilt: in den Pivot-Spalten ist nur noch der Pivot-Koeffizient von Null verschieden, und alle Pivot-Koeffizienten sind gleich 1.

Der Maple-Befehl heißt: gaussjord(A)

Satz 1": Durch Multiplikation von links mit einer invertierbaren (m×m)-Matrix kann jede Matrix mit Koeffizienten in einem Körper in Schubert-Normalform gebracht werden.

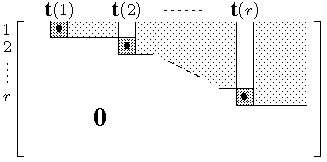
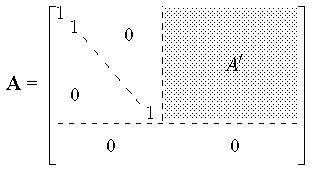
Satz 1"': Durch Multiplikation von links mit einer invertierbaren (m×m)-Matrix und eine Permutation der Spalten kann jede Matrix mit Koeffizienten in einem Körper in eine Schubert-Normalform mit Pivot-Spalten 1,2,...,r gebracht werden:

Satz 1"": Durch Multiplikation von links mit einer invertierbaren (m×m)-Matrix und von rechts mit einer invertierbaren (n×n)-Matrix kann jede Matrix mit Koeffizienten in einem Körper in die folgende Form gebracht werden:

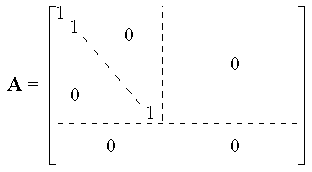
Beweis: Wir beginnen mit einer Schubert-Normalform. Durch Spalten-Vertauschungen (also Multiplikation von rechts mit einer Permutations-Matrix) erreichen wir, dass die Pivot-Spalten die Spalten 1,2,..,r sind.

Durch Addition des (-a_ij)-ten Vielfachen der i-ten Spalte mit 1≤i≤r zur j-ten Spalte mit r+1≤j≤n erreichen wir, dass der (i,j)-Koeffizient Null wird. Dies ist Rechtsmultiplikation mit der Elementar-Matrix I-a_ijE_ij.