• Der Satz von Dirichlet über Primzahlen in arithmetischen Progressionen:
  Satz. Sei (a,n) = 1. Dann gibt es unendlich viele Primzahlen p ≡ a mod n.
  Beweise, siehe:
  • Dickson: Modern Elementary Theory of Numbers (1939), Appendix
  • G.J.O.Jameson: The Prime Number Theorem. London Math. Soc. Student Texts 53 (2003), 4.
  • Scheid: Zahlentheorie, VI.5
• Der Primzahlsatz
  π(x) ~ x/ln(x), oder auch: π(x) ~ li(x).
  Beweise, siehe:
  • Bundschuh: Einführung in die Zahlentheorie. Kapitel 7.3.
  • G.J.O.Jameson: The Prime Number Theorem. London Math. Soc. Student Texts 53 (2003), 6.
  • Hua: Introduction to Number Theory (1982), Kaitel 9
  • Scheid: Zahlentheorie, VI.3
• Die Riemann'sche ζ-Funktion. (mit Konvergenz für reelle r > 1). Die Werte ζ(2t) für t in N:
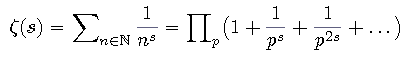
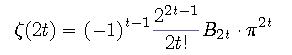
  Dabei ist
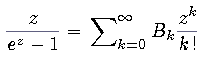
  Die Zahlen B_t sind rationale Zahlen, zum Beispiel:
  
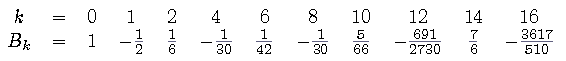
  (und B_2t+1 = 0 für t ≥ 1).
  • G.J.O.Jameson: The Prime Number Theorem. London Math. Soc. Student Texts 53 (2003), - 5.
  • Zagier: Zetafunktionen und quadratische Körper. Springer-Verlag 1981.

• Kettenbruch-Entwicklung
  • Bundschuh: Einführung in die Zahlentheorie. Kapitel 5.3
• Irrationalität und Transzendenz reeller Zahlen.
  • Bundschuh: Einführung in die Zahlentheorie. Kapitel 5.2 und Kapitel 6.

• Ergänzungen zum Legendre-Symbol: Jacobi-Symbol.

Themen, die im Rahmen der Vorlesung "Algebraische Zahlentheorie" angesprochen werden

• Die Pell'sche Gleichung: Ist d in N kein Quadrat, so hat die Gleichung X² - dY² = 1 unendlich viele Lösungen.
  • Bundschuh: Einführung in die Zahlentheorie. Kapitel 4.3
• Ganz allgemein: Quadratische Zahlkörper.

Ausblicke

• Komplexe Zahlen, Quaternionen, Oktonen:
  Summen von zwei, vier, acht Quadraten.
  Siehe etwa: John H. Conway, Derek A. Smith: On Quaternions and Octonions.
  Their Geometry, Arithmetic, and Symmetry. Peters, Wellesley/Mass 2003.
• Additive Zahlentheorie
  Partitionen
  • Scheid VII, Niven-Zuckerman 10.