BIREP: Representation Theory of Algebras: Striking New
Results. (Compiled by C.M.Ringel)
Example Nr.1
Rhombal Algebras
References:
Michael Steven Peach: Rhombal algebras and derived equivalences. Thesis. Bristol 2004.
Download
Joseph Chuang: Lecture at Beijing, May 2005.
W. Turner: On seven families of algebras.
Download.
And a paper by Chuang and Turner in preparation, devoted to a further
study of higher dimensional analogues.
This is an interesting
construction of (non semisimple) algebras which are both self-injective and
quasi-hereditary.
(If you want to protest that this is impossible, then be aware
that we deal with an algebra without 1, but with sufficiently many idempotents -
say with the path algebra of an infinite quiver with relations such that
all indecomposable projective and all indecomposable injective modules are
finite-dimensional; see also the example below.)
Here is the definition of the rhombal algebra A(Γ):
- Start with a tiling Γ of the plane using congruent rhombuses, for example with
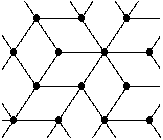
- Replace any edge of Γ by a pair of arrows in opposite direction, this is a quiver
(infinite, but locally finite, connected).
- Take the following quadratic relations:
- Paths of length 2 can be non-zero only if there exists at least
one rhombus which contains the two arrows involved in the path
on its boundary.
- Two paths of length 2 going from a vertex of a rhombus to the opposite vertex of this rhombus
add up to zero.
- Given a vertex x, there may be at most six paths of length 2 which go to a neighbor and return.
Add such a path and the path in the opposite direction (if they exist, otherwise use zero).
This gives three elements ax, bx, cx of the
path algebra. Take as relations: ax-bx and bx-cx.
(The signs used here differ from those in the thesis,
they are due to Turner.)
The Loewy factors of the indecomposable projective modules:
All the indecomposable projective modules have Loewy length 5, with socle isomorphic to the top
(in fact, A(Γ) is "graded symmetric").
If a vertex x has n neighbors (n=3,4,5,6), then the indecomposable projective module P(x)
has length 4n; its composition factors belong to the rhombuses which contain x. Here
are all the Loewy factors:
x
the neighbors of x
|
(n-2) copies of x and in addition all the vertices opposite to x
| the neighbors of x
| x
| | | |
(the "vertices opposite to x" refers to the vertices in the rhombuses which contain x).
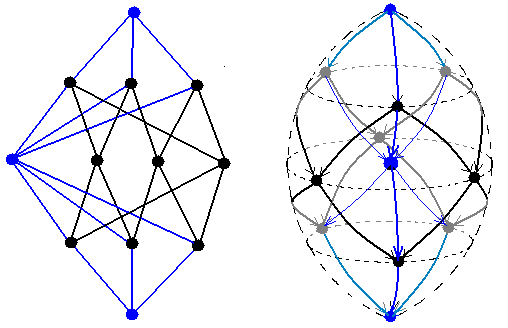
| Here are two different visualizations for the composition factors of P(x)
in the case n=3,
the blue vertices being
the composition factors of the form S(x):
| 
|
For n = 4,5,6, the composition factors are arranged as follows; with the big blue ellipse in the
middle layer consisting of n-2 composition factors S(x).
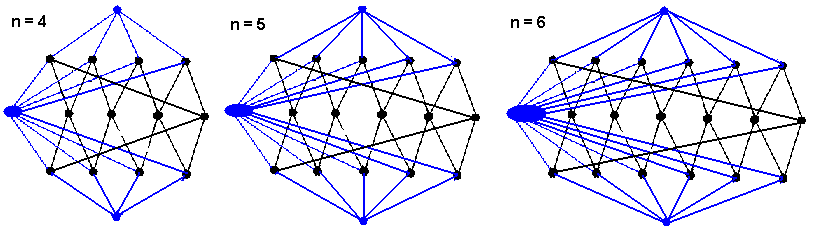
In order to get a heredity structure, take for any rhombus R
the four-dimensional module with top the marked red vertex x,
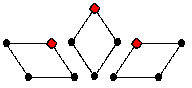with socle the opposite vertex y, and
using the two paths of length 2 from x to y; this will be the standard module Δ(x).
(There are six different ways of ordering the vertices in order to get a heredity structure; this one
is related to the direction "north", the remaining ones are obtained from this by rotation.)
If we attach to each rhombus R the corresponding red vertex x = v(R), we obtain a bijektion v
between the set of rhombuses and the set of vertices. For any vertex x, the indecomposable projective
module P(x) has a filtration with factors Δ(v(R)), where R runs through all the rhombuses
which contain x.
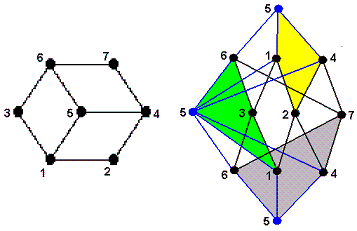
| Let us exhibit the standard filtration say of P(x), where x has three
neighbors (on the left, we show a corresponding local numbering of the vertices):
| 
|
The algebra A(Γ) is a Koszul algebra.
There is a nice tilting procedure,
replacing a given hexagon triple of rhombuses by its flip:
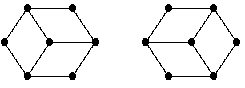It is given by a tilting complex concentrated at -1 and 0 (see Peach, Theorem 5.2.5).
In case we start with a periodic tiling Γ we obtain a Galois covering of a finite-dimensional
symmetric algebra (where we can visualize the vertices and arrows as living on a torus).
For example the following fundamental region gives rise to a self-injective algebra with 4 simple modules:
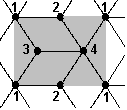here, the indecomposable projective modules P(x) have the following length:
x 1 2 34
| length of P(x) | 20 | 12 | 12 | 20
|
|---|
| | | | |
|---|
The main importance of the algebras A(Γ) stems from the fact that they are strongly
related to blocks B of group algebras (in characteristic p > 2)
of the symmetric groups with elementary abelian defect group
of order p2.
- There is a "large" idempotent e of B and an idempotent f of some rhombal algebra A(Γ)
such that eBe and fA(Γ)f are Morita equivalent.
("large" means that the idempotent kills only few simple modules).
- Any indecomposable projective B-module P has Loewy length ; the socle filtration of P
coincides with the radical filtration, and rad P/rad2 P is isomorphic to
rad3 P/rad4 P; the Jordan-Hölder multiplicities of P are
bounded as follows:
3 ≤ [P(x):S(x)] ≤ 6 and
[P(x):S(y)] ≤ 2 for y ≠ x.
- The quiver of B has no loops and multiple arrows.
Self-injective quasi-hereditary algebras:
Here is a more simple example of a
non semisimple algebra which is both self-injective and
quasi-hereditary:
this kind will be given by the quiver with
vertex set Z, with arrows α : i → i+1 and β : i+1 → i,
and with relations α2 = 0, β2 = 0, and αβ + βα = 0.
Here the indecomposable projectives are of length 4, with composition factors
whereas the standard modules are of length 2 with composition factors
(also this example is a special case of the algebras considered by Turner,
namely the case r=2: a "1-dimensional rhombal algebra").
Fakultät für Mathematik, Universität Bielefeld
Verantwortlich: C.M.Ringel
E-Mail:
ringel@math.uni-bielefeld.de
Last modified: Thu Jun 9 14:11:14 CEST 2005