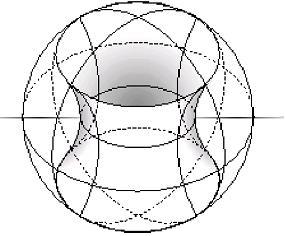
Two unit circles in S3, one in the x-y plane and the other in the z-w plane, form the basis of a curious structure on S3. The surface of a tubular neighborhood in a fixed distance from either of these circles forms a torus in S3. The Clifford Tori are the family of tori generated by tubular neighborhoods around either of these centerlines. A tubular neighborhood at a distance of n from one centerline is the tubular neighborhood at a distance of 1-n from the other, where 0 ≤ n ≤ 1. The family of tori generated by varying n are called the Clifford Tori. The tubular neighborhood at a distance of 1/2 forms the flat torus in S3 may be called the equatorial torus, because, like an equator, it divides the sphere neatly into two identical pieces

Note that T2 can be embedded in R4 so that it is "flat", that is, so that it's Gaussian curvature is 0 at every point. This is not possible in R3. The Clifford Tori are embedded "flatly" in S3 (considered as a subset of R4).
We consider a curious property of the sphere S3, the Hopf fibration. First we will consider a fibration on the torus T2, and then examine what it looks like when this fibration is extended to the Clifford Tori.
We can think of T2 as a square, or as I × I, with edges identified. Each pair of parallel and identified edges becomes one of the generators. First, draw a diagonal from one corner to it's opposite. Now, draw a series of lines parallel to that diagonal.
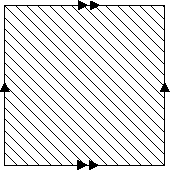
Now consider what these lines become when the square is wrapped up into a torus. They become a series of circles, each one circling the torus exactly once in the direction of one generator, and once in the direction of the other generator. Notice that the circles are linked, each one passing through each other one.
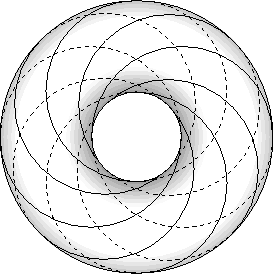
Now, consider if each of the Clifford Tori had this fibration on them. This is the Hopf Fibration. As the tubular neighborhood of these centerlines is shrunk, the tori get smaller, and the linked circles more closely approximate one of the centerlines.