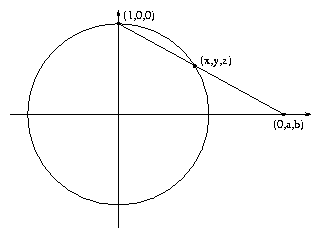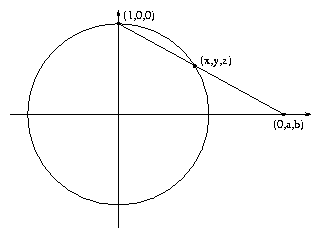The Hopf fibration
The Hopf fibration is a certain map h :S3 → S2, which
is a fundamental example in differential geometry and algebraic
topology. Here S2 is just the unit sphere in R3, given by the
familiar equation
The space S3 is the analogue one dimension higher: it is the
subspace of R4 given by the equation
Given a point (w,x,y,z) ∈ S3, we can form the complex number
(w+ix)/(y+iz) (provided that we allow the value ∞ when
y = z = 0). There is a well-known way of identifying C ∪ {∞}
(the "Riemann sphere") with S2: the point a+ib ∈ C gets
identified with the point where the line joining (1,0,0) to
(0,a,b) passes through S2, as shown in the following diagram.
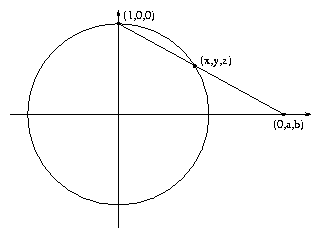
This is called "stereographic projection". With this
identification, we can define the Hopf map by
To get a geometric picture of this, we use stereographic projection
one dimension higher to identify S3 with R3 ∪
{∞}, and
thus to identify R3 with a subspace of S3, and thus to consider
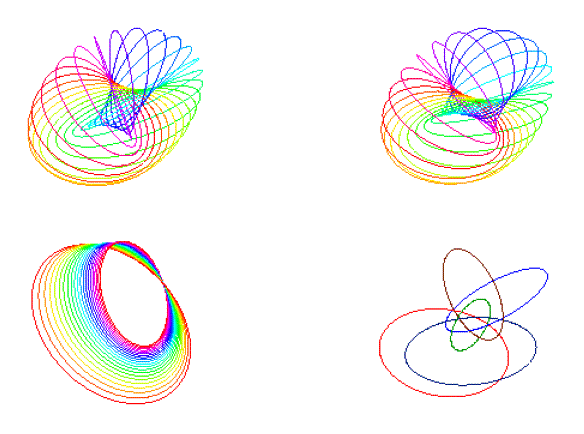
h as a map from R3 to S2. For any point c ∈ S2, the
preimage Cc: = h-1{c} is thus a subset of R3. It turns
out that Cc is always homeomorphic to the circle S1 (with one
exception due to the deleted point at ∞). It is a remarkable
geometric fact that any two of these circles are linked; the
circles have to be lined up in a very delicate way to ensure this.
The following diagram displays various families of Cc's:
The map h also plays an interesting role in homotopy theory.
There is a natural group structure on the set
π3(S2) of homotopy
classes of maps from S3 to S2. It turns out that this
group is
isomorphic to Z, and is generated by h; this was the first
example to be calculated of a group πn(Sm) with
n > m.
Another interesting fact is that h is the attaching map for the
four-dimensional manifold CP2 (the space of one-dimensional
subspaces of the complex vector space C3). More precisely,
if we
start with the four-dimensional ball B4 and identify a with b
whenever a,b ∈ S3 ⊂ B4 and h(a) = h(b), then the
resulting quotient space is homeomorphic to CP2.
Quelle:
Sheffield