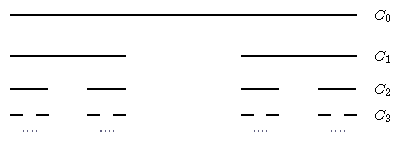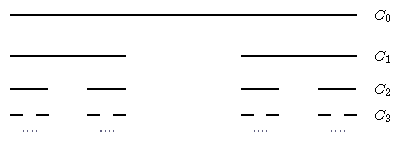Das Cantor'sche Diskontinuum
Wir bilden den Durchschnitt C der Mengen Ct, dabei entsteht Ct aus dem Einheitsintervall auf folgende
Weise: Teile [0,1] in 3t gleichlange Intervalle, und entferne
gewisse offene Intervalle Ui =
]i/3t,(i+1)/3t[, und zwar wird
Ui entfernt, falls in der triadischen Entwicklung von i
eine 1 vorkommt.
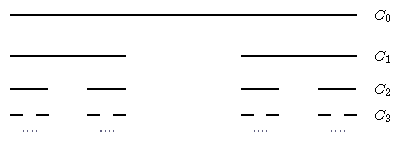
Wichtige Eigenschaften:
- C ist abgeschlossene (und beschränkte) Teilmenge von R, also kompakt.
- C ist total unzusammenhängend.
- C hat keine "isolierten Punkte" (es gibt keine einelementigen
offenen Teilmengen).