Hawaiischer Ohrring

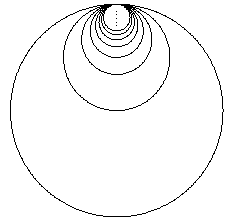
Man erhält X zum Beispiel als Bild X des Einheitsintervalls I unter einer Abbildung f: I → R², die das Intervall [1/i,1/(i+1)] auf den Kreis mit Radius 1/i und Mittelpunkt (0,-1/i) abbildet (und 1 auf x = (0,0)).

Eigenschaften:

• Jede Umgebung U von x enthält einen Unterraum A, der topologisch äquivalent zu S¹ ist und der ein Retrakt von U ist.
• Daraus folgt: x besitzt keine einfach-zusammenhängende Umgebung.
• Ist U eine beliebige Umgebung von x, so gibt es Schleifen in Ω(U,x), die in X nicht nullhomotop sind. (Also: X ist nicht semi-lokal-einfach-zusammenhängend.)

• X ist kompakter Hausdorff-Raum.
• H₁(X) ist nicht endlich erzeugt.
  Denn für jedes t ist die punktierte Summe von t Kreisen ein Retrakt von X.
• Demnach gilt: X ist kein CW-Komplex.
  Denn jeder kompakte CW-Komplexe hat endlich erzeugte Homologie.