Polnischer Kamm
Sei B die Menge der Punkte der Form (1/n,0) mit n in
N zusammen mit x = (0,0).
Betrachte den Unterraum K der reellen Ebene, der dadurch entsteht, dass
man die Punkte der Menge B mit dem Punkt p = (0,1) gradlinig verbindet.
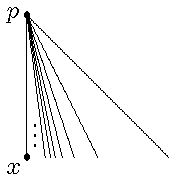
Eigenschaften:
- K ist nicht lokal zusammenhängend.
- (K,p) ist zusammenziehbar.
- (K,x) ist nicht zusammenziehbar.
Verdoppelung
L entstehe aus K durch Hinzunahme aller Punkte (x,y) mit (-x,-y) in K.
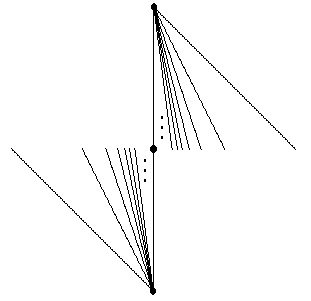
Eigenschaften:
- L ist nicht lokal zusammenhängend.
- L ist nicht zusammenziehbar.
- Alle Homotopiegruppen sind Null.
Also ist die Einbettung eines jeden Punkts eine schwache
Homotopie-Äquivalenz, aber keine Homotopie-Äquivalenz
(siehe Maunder: Algebraic Topology, Example 7.5.5).

