Topologie: Linsen-R&aum;ume

Linsen-Räume L(p,q)

Seien p,q relative prime natürliche Zahlen. Sei ε = e^2πi/p primitive p-te Einheitswurzel.

Erste Definition

Betrachte im R³ folgendes Polyeder P: Nimm in der x-y-Ebene die Potenzen z_i = εⁱ mit 0 ≤ i ≤ p-1 (sie bilden ein regelmäßes p-Eck) und die Punkte N = (0,0,1) und S = (0,0,-1). Bilde die konvexe Hülle dieser Punkte (dies ist ein Raum, der homöomorph zum 3-Ball ist). Der Rand von P besteht aus 2p kongruenten Dreiecken.

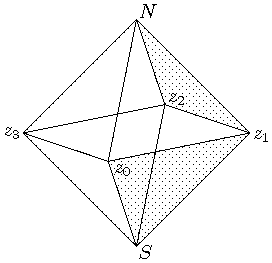
Identifiziere das Dreieck z_iz_i+1N mit dem Dreieck z_i+qz_i+q+1S (dabei betrachte die Indizes modulo p). Dies liefert eine geschlossene 3-dimensionale Mannigfaltigkeit, den Linsenraum L(p,q).
Hier der Fall p=4.
Punktiert sind die Dreiecke z₁z₂N und z₀z₁S,
die für q=3 zu identifizieren sind.

Zweite Definition

Betrachte die primitive p-te Einheitswurzel ε = e^2π/p und die von ε erzeugte Gruppe C_p = {1,ε,...ε^p-1}. Die Gruppe C_p operiere auf der 3-Sphäre wie folgt: Wir fassen S³ als Unterraum von C² auf, nämlich als die Menge aller Paare (z₁,z₂) mit |z₁|² + |z₂|² = 1, und es sei ε*((z₁,z₂) = (εz₁,ε^qz₂) Setze L(p,q) = S³/C_p Dies ist eine eigentlich-diskontinuierliche Gruppen-Operation, also ist die Projektionsabbildung S³ → L(p,q) eine Überlagerung.

Gegeben ist hier die universelle Überlagerung S³ → L(p,q).

Eigenschaften

π₁(L(p,q),*) = C_p,
denn die Projektionsabbildung S³ → L(p,q) ist universelle Überlagerung.
Die ganzzahligen Homologie- und Kohomologie-Gruppen lauten:

i 0 1 2 3
H_i Z C_p 0 Z
Hⁱ Z 0 C_p Z

i	0	1	2	3
H_i	Z	C_p	0	Z
Hⁱ	Z	0	C_p	Z

Homöomorphie

Satz (Reidemeister 1935). Genau dann sind die Linsenräume L(p,q) und L(p',q') homöomorph, wenn gilt:

p = p' und
q ≡q' (mod p) oder q ≡-q' (mod p) oder qq' ≡1 (mod p) oder qq' ≡-1 (mod p).