Topologie

Metrische Räume

Eine Metrik auf einem topologischen Raum X liefert nicht nur die Topologie von X, sondern auch eine Vervollständigung von X.
Man nennt zwei Metriken äquivalent, wenn sie die gleiche Topologie liefern.
Äquivalente Metriken können völlig verschiedene Vervollständigungen liefern!

Zur Verdeutlichung hier einige Metriken auf X = R zusammen mit den zugehörigen Vervollständigungen.
Oder genauer: Wir skizzieren die Vervollständigung, jeweils als Teilmenge des R²: schwarz gezeichnet ist X, die roten Punkten gehören zur Vervollständigung, nicht aber zu X.

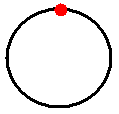
R mit der üblichen Metrik.

Die Metrik des offenen Intervalls ]0,1[

Die Metrik von S¹-{*}

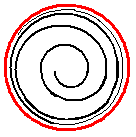
Die Metrik der Menge {(x,sin(1/x)| x > 0}

(also jeweils Folgen schwarzer Punkte, die gegen einen roten Punkt konvergieren).

Hier noch ein weiteres Beispiel, das genau zwei zusätzliche Limespunkte von Cauchy-Folgen besitzt (wie das offene Intervall ]0,1[; aber die Metriken sind völlig verschieden):

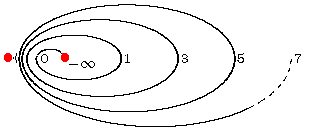
Die Zahlen deuten eine Parametrisierung dieser Kurve an: dabei soll die Menge 2N der positiven geraden Zahlen eine Cauchy-Folge sein, der linke rote Punkt sei ihr Limespunkt (nur 0 ist markiert, links davon solte eine 2, eine 4, eine 6, ... stehen). Dagegen ist zum Beispiel die Menge der positiven ungeraden Zahlen keine Cauchy-Folge.

		R mit der üblichen Metrik.
		Die Metrik des offenen Intervalls ]0,1[
		Die Metrik von S¹-{*}
		Die Metrik der Menge {(x,sin(1/x)\| x > 0}