sin(1/x)
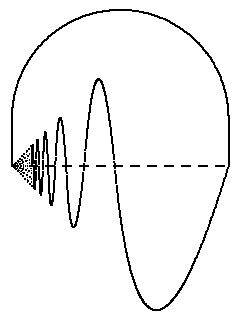
Betrachte folgende Unterräume X', X", X der reellen Ebene:
- Sei X' der Graph der Abbildung sin(1/x): R+
→ R
- sei X" die Menge der Punkte (0,y) mit -1 ≤ y ≤ 1.
- Sei X die Vereinigung von X' und X".
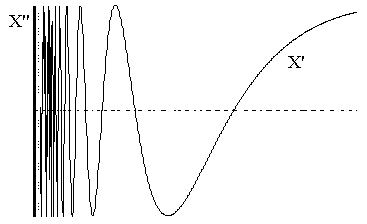
Eigenschaften:
- X' ist topologisch äquivalent zu R+ und
X ist der Abschluss von X in der Ebene.
- X ist zusammenhängend.
- X ist nicht lokal zusammenhängend.
- X ist nicht weg-zusammenhängend: es gibt genau zwei
Wegzusammenhangs-Komponenten
Die Menge π0(X) der Wegzusammenhangs-Komponenten von
X mit der Quotiententopologie besitzt genau drei offene Mengen.
Der polnische Kreis
Hier ein ähnlicher Raum Y, ebenfalls ein Unterraum der reellen Ebene
- Y' sei der Graph der Abbildung sin(1/x): ]0,1/π]
→ R
- Y" sei der Kurvenzug, der aus der Strecke der Punkte
(0,y) mit -1 ≤ y ≤ 1, dem oben Halbkreis mit Mittelpunkt
(1/(2π),1) und Radius 1/(2π) und der Strecke mit den Punkten
(1/π,y), mit 0 ≤ y ≤ 1, besteht.
- Sei Y die Vereinigung von Y' und Y".
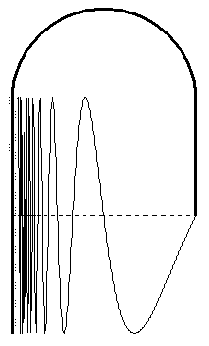
Eigenschaften:
- Y ist weg-zusammenhängend,
- Y ist nicht lokal zusammenhängend.
- Sei X der Unterraum aller Punkte (0,y) mit -1 ≤ y ≤ 1, dies ist
ein Intervall. Es ist Y/X homöomorph zum Kreis S1,
denn die Abbildung x.sin(1/x) : [0,1/π] → R liefert
einen Homöomorphismus zwischen dem Intervall [0,1/π] und dem Graph
dieser Abbildung.
Also gilt:
H1(Y/X) = Z, dagegen: H1(Y,X) = 0,
Hier ein Bild von Y/X: