Whiteney's Regenschirm
"Whitney's Regenschirm" ist ein Rechteck R mit einer Abbildung f:R → R3, die keine topologische Immersion ist; dabei gibt es genau
einen Punkt x in R, den man entfernen muss, will man eine topologische
Immersion erhalten!
Abbildung

Siehe auch:
Whitney's Regenschirm (Animation)
(Aus Eric Weisstein's world of Mathematics))
Simpliziale Version
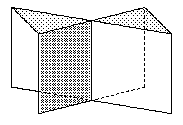
Beschreibung
Sei R das folgende (ein wenig "verzogene") Rechteck in der Ebene R2.
Whitney's Regenschirm ist die durch die Skizze gegebene
(simpliziale) Abbildung f:R → R3 mit Bild W.
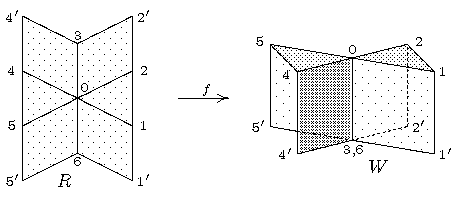
- Dies ist keine topologische Immersion,
denn im Punkt x=0 gilt: Ist U eine beliebige
Umgebung dieses Punkts, so ist die Einschränkung f|U nicht injektiv
(unter f wird ja jeder Punkt der Kante [0,3] mit einem Punkt der Kante [0,6]
identifiziert, die Umgebung U enthält also Punkte, die unter f
identifiziert werden!)
- Jeder von x verschiedendene
Punkt y in R besitzt dagegen eine Umgebung V, so dass die Einschränkung
von f auf V ein Homöomorphismus V → f(V) ist.
Entfernen wir also den Punkt x=0, so gilt: die Einschränkung von f
auf R-{x} ist eine topologische Immersion.


