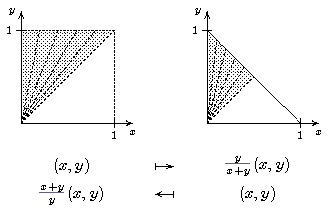- Sei (X,T) ein topologischer Raum und T' ⊆ T, so dass auch (X,T') wieder ein topologischer Raum ist. Dann ist die identische Abbildung id: (X,T) → (X,T') stetig. Ist aber T' eine echte Teilmenge von T, so ist die Umkehrabbildung nicht stetig!
- e2πix: [0,1[ → S1. (Andere Beschreibung: Sei I = [0,1], und betrachte die Quotienten-Abbildung (siehe Kapitel 3) p: I → I/~, die die Endpunkte von I identifiziert. Die Einschränkung von p auf [0,1[ ist bijektiv und stetig, ihre Umkehrabbildung ist aber nicht stetig.)
- f0(x) = (x,x) für alle x ∈ I.
- Um f1 zu definieren, werde I in 9 gleich lange
Strecken geteilt, also in die Teilintervalle [(i-1)/9,i/9] mit
1 ≤ i ≤ 9. Entsprechend wird I×I in 9
gleich große Quadrate geteilt. Diese Quadrate werden
geeignet durchnummeriert (siehe das Bild n=1),
und das i-te Intervall [(i-1)/9,i/9] wird
nun unter f1 in das i-te Quadrat abgebildet, und zwar werden die
einzelnen Teilintervalle jeweils auf Diagonalen abgebildet.
(Durch die Forderungen,- dass f1 stetig ist,
- dass f1(0) = (0,0) gilt,
- dass die 9 Einschränkungen auf die Teilintervalle linear sind
- und dass wir jeweils erst horizontal, dann vertikal laufen,
- Um f2 zu definieren, werde I in 92 gleich lange Strecken geteilt. Entsprechend wird I×I in 92 gleich große Quadrate geteilt. Die Nummerierung erfolgt wie im Bild n=2 angedeutet (Man läuft innerhalb der 9 Teilquadrate des Schritts n=1 jeweils erst horizontal, dann vertikal.), und unter f2 wird wieder das i-te Intervall in eine Diagonale des i-ten Quadrats abgebildet.
-
Allgemein: Um fn zu definieren, werde I in 9n gleich lange
Strecken geteilt. Entsprechend wird I×I in 9n
gleichgroße Quadrate geteilt. Die Nummerierung der Quadrate
erfolgt induktiv. Man läuft jeweils erst horizontal, dann vertikal.
Unter fn wird das
i-te Intervall in eine Diagonale des i-ten Quadrats
abgebildet.

Es ist einfach zu sehen: Die Funktionenfolge fn konvergiert gleichmäßig gegen eine Funktion f (die natürlich wieder stetig ist). Dies ist die gesuchte Peano-Kurve.
Es gilt:
- Ist x = a/9n, wobei a eine natürliche Zahl mit 0 ≤ a ≤ 9n ist, so ist fm(x) = fn(x) für alle m ≥ n, also auch f(x) = fn(x).
- f ist surjektiv. Zum Beweis reicht es zu zeigen, dass das Bild von f dicht ist. (Denn nach Satz 2 ist das Bild abgeschlossen: I ist kompakt, f ist stetig, und I×I ist Hausdorffsch.) Es liegen alle Paare (a/3n,b/3n) mit natürlichen Zahlen a,b ≤ 3n im Bild von fn, also nach 1. auch im Bild von f. Die Menge dieser Paare (a/3n,b/3n) (mit n beliebig) ist aber dicht in I×I.
- f ist nicht injektiv: Jedes Paar (a/3n,b/3n) mit 0 < a,b < 3n hat genau zwei Urbilder, die übrigen Elemente von I×I haben nur ein Urbild.
|
Warnung 1: Eine bijektive, stetige Abbildung
ist nicht immer ein
Homöomorphismus. Ganz allgemein muss man aufpassen:
Ist f eine stetige Abbildung, so ist das Bild einer offenen
Menge
nur selten wieder offen!
Es gibt viele Beispiele: |
|
Warnung 2: Die Existenz surjektiver stetiger
Abbildungen X → Y, Y → X impliziert nicht,
dass X und Y topologisch äquivalent sind.
Beispiel: Eine Peano-Kurve ist eine surjektive stetige Abbildung I → I×I (siehe unten). Und natürlich gibt es surjektive stetige Abbildungen I×I → I. Aber I und I×I sind nicht topologisch äquivalent. (Entfernt man einen beliebigen Punkt aus I×I, so bleibt der Raum zusammenhängend; entfernt man dagegen aus I den Punkt 1/2, so erhält man zwei Zusammenhangskomponenten.)
Konstruktion einer Peano-KurveWir definieren stetige, stückweise lineare Abbildungen fn : I → I×I mit fn(0) = (0,0) und fn(1) = (1,1) auf folgende Weise: |
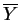 - Abschluss von Y, Yo -
offener Kern von Y, ∂Y - Rand von Y
- Abschluss von Y, Yo -
offener Kern von Y, ∂Y - Rand von Y
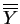 =
=