Die Noether'schen Isomorphie-Sätze

Wir betrachten hier beliebige (nicht notwendig kommutative) Gruppen, schreiben aber die Griuppenoperation als + (da unser Interesse hier vor allem abelschen Gruppen gilt). Für die hier formulierten Aussagen gibt es ganz entsprechende Aussagen im Fall von R-Moduln, dabei sei R ein beliebiger (nicht notwendig kommutativer) Ring.

Ist A' ein Normalteiler der Gruppe A, so kann man die Faktorgruppe A/A' bilden: die Elemente von A/A' sind die Restklassen [a] = a+A' der Elemente von A, und man definiert [a] + [b] = [a+b] für a,b in A (zu zeigen ist: dies ist wohldefiniert, und A/A' ist wieder eine Gruppe).

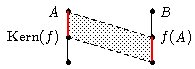
Erster Isomorphiesatz

Dieser Satz wird üblicherweisen durch folgende Skizze veranschaulicht:

Folgender Spezialfall ist essentiell:

Ist f : A → B ein bijektiver Gruppenhomomorphismus, so ist f ein Isomorphismus.

(Für einen bijektiven Gruppenhomomorphismus f ist Kern(f) = 0, daher handelt es sich hier wirklich um einen Spezialfall).
Zum Beweis des ersten Isomorphiesatzes beweist man zuerst den genannten Spezialfall:
Sei also f ein bijektiver Gruppen-Homomorphismus. Zu zeigen ist, dass die (mengentheoretische) Umkehrabbildung f^-1 ein Gruppenhomomorphismus ist. Aber aus f(a+a') = f(a) + f(a') für alle a, a' in A folgt f^-1(b+b') = f^-1(b)+f^-1(b') für alle b, b' in B.
Ist nun f : A → B ein beliebiger Gruppen-Homomorphismus, so ist zu erst zu eigen, dass der Kern A' = Kern(f) von f ein Normalteiler ist. Die von f induzierte Abbildung A/A' → f(A) ist ein bijektiver Gruppen-Homomorphismus, also ein Isomorphismus.

Allgemeiner gilt:

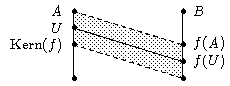
Ist U eine beliebige Untergruppe von A, so ist f-1f(U) = U+A'. Ist V eine beliebige Untergruppe von B, so ist ff-1(V) = V∩f(A).

Insbesondere zeigen diese Formeln: ist A' ⊆ U, so ist f^-1f(U) = U.
Ist V ⊆ f(A), so ist ff^-1(V) = V.

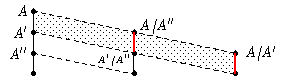
Dritter Isomorphiesatz. Seien A" ⊆ A' ⊆ A Normalteiler der Gruppe A. Dann liefert die Zuordnung, die [[a]] = (a+A")+(A'/A") die Restklasse [a] = a+A' zuordnet, einen Isomorphismus (A/A")/(A'/A") → A/A'.

Beweis: Die Abbildung A/A" → A/A', die der Restklasse a+A" die Restklasse [a] = a+A' zuordnet, ist wohldefiniert. Dies ist ein surjektiver Gruppen-Homomorphismus, dessen Kern gerade A'/A" ist. Also folgt die Behauptung aus dem ersten Isomorphiesatz.

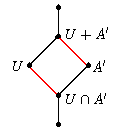
Zweiter Isomorphiesatz. Ist A' ein Normalteiler der Gruppe A und U eine Untergruppe von A, so ist U∩A' ein Normalteiler von U, und die Gruppen U/(U∩A') und (U+A')/A' sind isomorph.

Die kanonische Abbildung U → (U+A')/A' ist surjektiv und ihr Kern ist U∩A'. Also zeigt der erste Isomorphiesatz, dass die induzierte Abbildung U/(U∩A') → (U+A')/A' ein Isomorphismus ist.

Modularität

Beweis: Die Inklusion U+(V∩W) ⊆ (U+V)∩W gilt ganz allgemein für beliebige Untergruppen U,V,W einer Gruppe; die Voraussetzung U ⊆ W wird für die umgekehrte Inklusion gebraucht:
Sei u+v = w (mit u in U, v in V, w in W) ein Element von (U+V)∩W. Dann ist v = -u+w ein Element von W, also von V∩W. Also ist u+v in U+(V∩W).

Bemerkung. Unter der Voraussetzung U ⊆ W gilt sowohl U∩W = U als auch U+W = W, also kann man die Gleichung U+(V∩W) = (U+V)∩W auf folgende beide Weisen umschreiben:

• (U∩W)+(V∩W) = (U+V)∩W,
• U+(V∩W) = (U+V)∩(U+W),
also als Distributivgesetze - diese Distributivität gilt aber eben nur unter der Voraussetzung U ⊆ W.

Ganz allgemein gilt:

• (V₁∩W)+(V₂∩W) ⊆ (V₁+V₂)∩W,
• U+(V₁∩V₂) ⊆ (U+V₁)∩(U+V₂).
Dass die umgekehrten Inklusionen üblicherweise nicht richtig sind, sieht man am Beispiel der Unterräume des zweidimensionalen k-Vektorraums k² (k ein Körper): Sei V₁ = k×0, V₂ = 0×k, und U = W ={(x,x)| x in k}.

Subquotienten

"Subquotienten von Subquotienten sind Subquotienten".

Sei also A" ⊆ A' ⊆ A, und sei A" ein Normalteiler von A'. Sei B = A'/A". Sei B" ⊆ B' ⊆ B, und sei B" ein Normalteiler von B'. Betrachte die kanonische Abbildung A' → A'/A" = B; wir bezeichnen sie mit f. Dann ist f^-1(B") ⊆ f^-1(B') der gesuchte Subquotient von A: denn f^-1(B"), f^-1(B') sind Untergruppen von A', die A" enthalten, und f^-1(B") ist ein Normalteiler von f^-1(B').

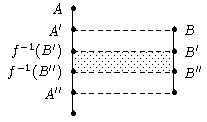
Beachte: Nach dem dritten Isomorphiesatz ist f^-1(B')/f^-1(B") zu B'/B" isomorph.