Für p in X und z in |X| sind also die folgenden beiden
Aussagen äquivalent:
|
| Hier als Beispiel
Links ein 2-Simplex, rechts die Sterne der drei Ecken: | 
|
| Ein komplizierteres Beispiel:
(Die Sterne sind jeweils rot markiert) | 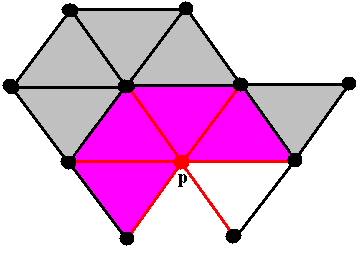
|
Lemma. Der Stern st(p) ist das Komplement in |X| der Vereinigung aller |σ|, wobei σ die Simplizes von X durchläuft, die p nicht enthalten.
- Beweis: Wir zeigen, dass die Vereinigung V aller |σ| mit p nicht
in σ, gerade das Komplement von st(p) ist.
Sei also z in V. Es gibt also ein Simplex σ das p nicht enthält,
sodass z zu |σ| gehört. Der
Träger von z ist eine Teilmenge von σ; da p nicht in σ
liegt, ist p nicht im Träger von z, also ist z nicht in
st(p). Ist umgekehrt z nicht in st(p), so ist
p nicht in tr(z). Also ist tr(z) ein Simplex, das p nicht enthält,
und das demnach an der Vereinigungsbildung teilnimmt: also |tr(z)| ist
Teilmenge von V. Da z zu |tr(z)| gehouml;rt, ist also z in V.
Eigenschaften.
- st(p) ist offen in |X|
(Denn das Komplement von st(p) ist Vereinigung endlich vieler abgeschlossener Teilmengen der Form |σ|.) - |X| ist die Vereinung der Sterne st(p), mit p in X.
(Denn für jedes z in |X| gibt es mindestens ein p mit p in tr(z).) - Also gilt: Die Teilmengen st(p) bilden eine offene Überdeckung von |X|.
- Hat jedes Simplex von |X| einen Durchmesser kleiner oder gleich d,
so hat jeder Stern st(p) einen Durchmesser kleiner oder gleich 2d.
(denn sind z, z' zwei Punkte in st(p), so gehören z und p zu einem Simplex, entsprechend gehören z' und p zu einem Simplex.)
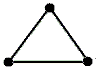 . Ist X ein beliebiger
1-dimensionaler Simplizialkomplex mit n Ecken, so sind alle
Abbildungen von der Eckenmenge von X in die Eckenmenge von Y simplizial,
es gibt also genau 3n simpliziale Abbildungen X → Y.
. Ist X ein beliebiger
1-dimensionaler Simplizialkomplex mit n Ecken, so sind alle
Abbildungen von der Eckenmenge von X in die Eckenmenge von Y simplizial,
es gibt also genau 3n simpliziale Abbildungen X → Y.
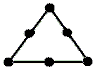 , so liefern die
36 simplizialen Abbildungen βY → Y
Abbildungen S1 →
S1
mit Abbildungsgrad -2, -1, 0, 1 und 2.
, so liefern die
36 simplizialen Abbildungen βY → Y
Abbildungen S1 →
S1
mit Abbildungsgrad -2, -1, 0, 1 und 2.