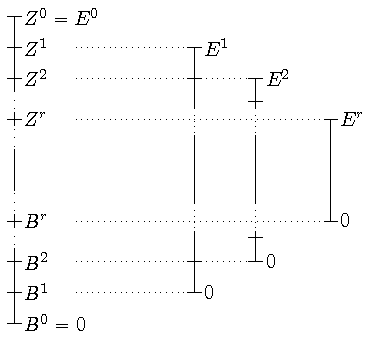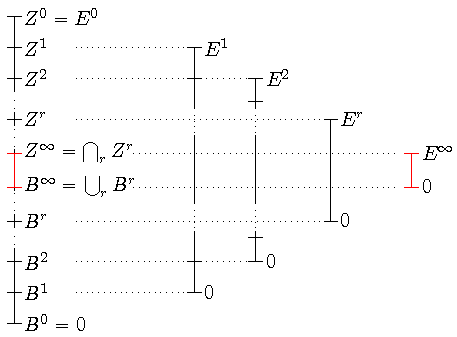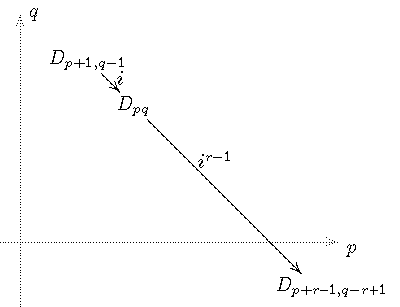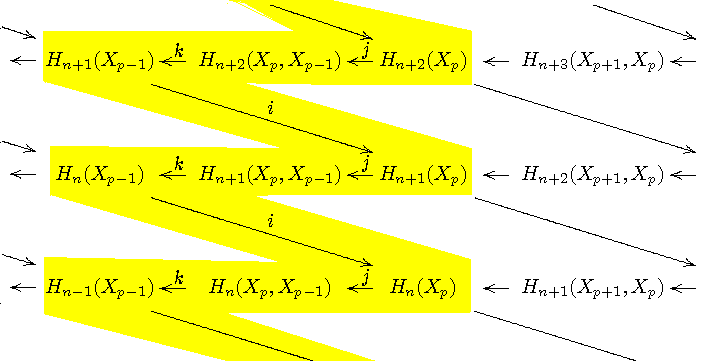Spektralfolgen

Definition: Eine bigraduierte abelsche Gruppe A = (A_pq)_pq ist eine Zuordnung, die jedem Paar (p,q) ganzer Zahlen eine abelsche Gruppe A_pq zuordnet (manchmal denkt man dabei auch an die direkte Summe ⊕ A_pq, fixiert dabei aber die gegebene direkte Zerlegung). Sind A, B bigraduierte abelsche Gruppen, so ist eine Abbildung f : A → B vom Bigrad (s,t) eine Familie von Gruppenhomomorphismen A_pq → B_p+s,q+t.

• Es ist (d^r)² = 0 und
• E^r+1 = H(E^r,d^r).

Man nennt (E^r,d^r) die r-te Seite von E.
Manchmal wird nur verlangt, dass die r-ten Seiten mit r ≥ k für ein k (etwa k = 1 oder k = 2) gegeben sind, man spricht dann von einer E^k-Spektralfolge, oder sagt, dass die Spektralfolge mit E^k beginnt.
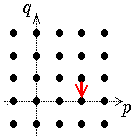
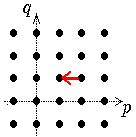
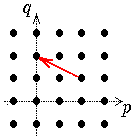
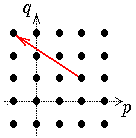
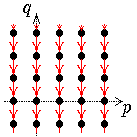
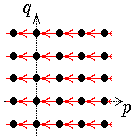
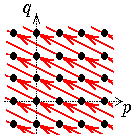
Jede Seite besteht aus abzählbar vielen Komplexen, die "quer über die Seite" laufen: die Steigung der Geraden, auf denen diese Komplexe liegen, ist von r abhängig, und zwar gleich (-r+1)/r.


	r=0	r=1	r=2	r=3
d21
alle dpq

Ist eine Spektralfolge E gegeben, so ist das Blatt E^r+1 ein Subquotient von E^r und demnach von E⁰: gegeben ist also eine Folge "ineinandergeschachtelter" Subquotienten von E⁰. Genauer kann dies folgendermaßen beschrieben werden: Induktiv definieren wir Untergruppen Z^r und B^r von E⁰ mit

• Z⁰ = E⁰
• B⁰ = 0.

• Z^r+1/B^r = Kern d^r
• B^r+1/B^r = Bild d^r

• Z^r+1/B^r+1 = E^r+1

(Es sei hier an die Regel erinnert: "Subfaktoren von Subfaktoren sind Subfaktoren".)

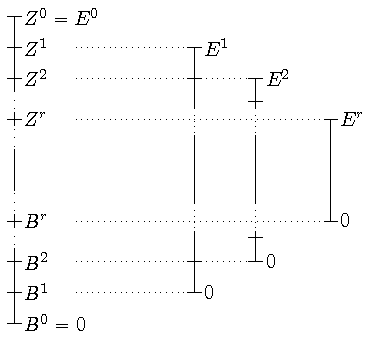
Konvergenz

• Z^∞ = ∩_r Z^r
• B^∞ = ∪_r B^r
• E^∞ = Z^∞/B^∞

Der Sprachgebrauch ist uneinheitlich: manchmal spricht man von "Konvergenz" nur dann, wenn es für jedes Paar (p,q) ein r = r(p,q) gibt mit Z^r_pq = Z^r+t_pq und B^r_pq = B^r+t_pq für alle t > 0 (sodass also gilt: Z^∞_pq = Z^r_pq und B^∞_pq = B^r_pq).

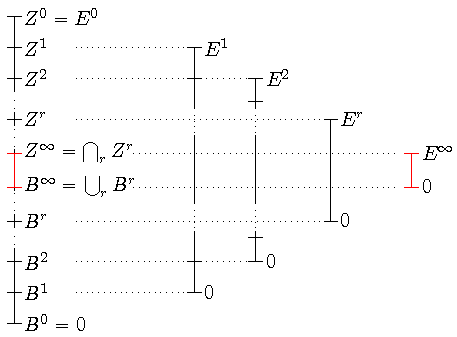
Lemma. Gilt für jedes Paar (p,q) in Z

Liegt Er im ersten Quadranten, so gilt: E∞pq = Erpq, falls r > p und r > q+1. (q = 0) Es ist E∞p0 = Ep+1p0 → ... → Er+1p0, → Erp0, und alle diese Abbildungen sind Monomorphismen. (p = 0) Es ist E∞0q = Eq+20q ← ... ← Er0q ← Er0q und alle diese Abbildungen sind Epimorphismen.

Alle drei Aussagen sind wichtig.
Die erste Aussage zeigt, dass es sich beim Konvergenz-Verhalten um einen Stabilisierungs-Prozess handelt:

Die jeweiligen Bereiche, die mit E∞ übereinstimmen (falls Er im ersten Quandranten liegt):
E2	E3	E4

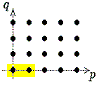
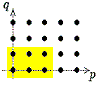
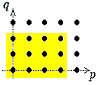
Die zweite Aussage dreht sich um das Verhalten für q=0, also für die Positionen auf der p-Achse

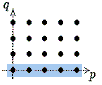
Die dritte Aussage dreht sich um das Verhalten für =0, also für die Positionen auf der q-Achse

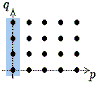
Beweis von (1): Für all s ≥ r liegt das Ziel von d^s_pq an der Stelle (p-s,p+s-1), und p-s ≤ p-r < 0; und betrachtet wird ja jeweils der Kern von d^s_pq. Das Ziel von d^s_pq liegt also außerhalb des ersten Quadranten.
Entsprechend hat man das Bild von d^s_p+s,q-s+1 zu betrachten, aber die Abbildung d^s_p+s,q-s+1 startet an der Stelle (p+s,q-s+1) und q-s+1 ≤ q-r+1 < 0. Der Start von d^s_p+s,q-s+1 liegt also außerhalb des ersten Quadranten.

Noch einmal: Wenn man beim "Blättern" der Seiten einer Spektralfolge die Vorstellung hat, dass die Seiten wie bei einem Buch über oder unter einander liegen, so ist dies falsch: die (r+1)-Seite ist ein Subquotient der r-ten Seite!

Komplexe mit Filtrierung

Jeder Komplex mit Filtrierung liefert eine Spektralfolge: Zrpq = {c in FpCp+q | ∂c in Fp-rC• } Erpq = Zrpq/ (Zr-1p-1,q+1 + ∂C• ∩ FrC•) dr sei durch ∂ induziert. Es gilt: E1pq = Hp+q(FpC•/Fp-1C•) und d1pq ist der Randoperator des Tripels (FpC•,Fp-1C•,Fp-2C•) E∞pq ist isomorph zur assoziierten graduierten Gruppe von Hp+q(C•) bezüglich der Filtrierung, die durch die Bilder der kanonischen Abbildungen Hp+q(FpC•) → Hp+q(C•) gegeben ist.

Exakte Paare (exact couples)

Eingeführt von Massey, Annals of Math (1952)

bigraduierten abelschen Gruppen D, E und Abbildungen i : D → D   - meist vom Bigrad (1,-1) j : D → E    - meist vom Bigrad (1-r,r-1) k : E → D   - meist vom Bigrad (-1,0)

(dieses Bild berücksichtigt nicht die Bigrade)

• die Folge D → D → E → D → D ist exakt.

Ist (D,E,i,j,k) ein exaktes Paar, so bildet man das abgeleitete exakte Paar (D',E',i',j',k') wie folgt:

• D = i(D)
• E = H(E,d) = Ker(d)/Bild(d)
• i' = i|D'
• j' = ji^-1, mit anschließender Restklassenbildung,
  (also für i(x) in D' mit x in D ist definiert j'i(x) = [j(x)] = j(x) + Bild(d) ).
• k' sei von k induziert (also k'([y]) = k(y), für y in E).

Beweis: Vieles ist zu zeigen, aber alles ist ganz einfach:
• j' ist eine Abbildung (j' ist für jedes x in D' definiert, wegen D' = i(D); j' ist wohldefiniert:
  seien x, x' in D mit i(x) = i(x'). Zu zeigen ist [j(x)] = [j(x')], dass also j(x)-j(x') zu Bild(d) gehört.
  Nun ist x-x' in Kern(i) = Bild(k), also etwa x-x' = k(y) mit y in E, und demnach j(x)-j(x') = j(x-x') = jk(y) = d(y).
  (Wir haben hier also die Exaktheit von (k,i) verwandt.)
• k' ist wohldefiniert (wegen kj = 0).
• j'i' = 0 (wegen ji = 0).
• k'j' = 0 (wegen kj = 0).
• i'k' = 0 (wegen ik = 0).
• Exaktheit von (i',j'). Wir betrachten ein Element i(x) in D', mit x in D, das zum Kern von j' gehört. Es ist also j(x) im Bild(d), etwa j(x) = jk(y) för ein y in E. Aus j(x-k(y)) = 0 folgt wegen der Exaktheit von (i,j) die Existenz eines x' in D mit x-k(y) = i(x'), also x = i(x')+k(y). Wenden wir i an, so erhalten wir i(x) = i²(x'), da ik = 0 ist. Also ist i(x) im Bild von i'.
• Exaktheit von (j',k'). Sei [y] in E' mit k'([y]) = 0. Dabei sei y im Kern(d). Wegen 0 = k(y) und der Exaktheit von (j,k) gibt es ein x in D mit i(x) = y. Das gesuchte Urbild von [y] unter j' ist i(x), denn j'i(x) = [ji^-1i(x)] = [j(x)] = [y].
• Exaktheit von (k',i'). Sei x in D' mit i'(x) = 0. Also x = i(x') für ein x' in D. Wegen der Exaktheit von (k,i) gibt es y in E mit k(y) = x. Es ist d(y) = jk(y) = j(x) = ji(x') = 0, also gehört y zum Kern von d und die Restklasse [y] von y modulo Bild(d) wird unter k' auf x abgebildet.

• D^r = i^r-1(D)
• D^r = Kern(d^r-1)/Bild(d^r-1)
• i^(r) = Einschränkung von i
• j^(r) = ji^r-1 mit anschließender Restklassenbildung
• k^(r) = induziert von k.

• d^(r) = j^(r)k^(r)

Offensichtlich gilt:

Jedes exakte Paar (Dr,Er,i,j,k) mit Bigraden (1,-1),(1-r,r-1),(-1,0) liefert (zusammen mit seinen Ableitungen) eine Er-Spektralfolge (Er,dr), (Er+1,dr+1), (Er+2,dr+2),...

Konvergenz der Spektralfolge eines exakten Paars

Wir setzen voraus: D_pq = 0 für p < 0.

Daraus folgt, dass auch E_pq = 0 für p < 0 gilt, denn (j,k) liefert eine exakte Folge D_pq → E_pq → D_p-1,q

Zusätzlich gilt für r > p:

• D^r_p-1,q = i^r-1(D_p-r,q+r-1) = 0,
  also ist k^(r)_pq : E^r_pq → D^r_p-1,q die Nullabbildung,
  und demnach ist j^(r)_p+r-1,q-r+1 : D^r_p+r-1,q-r+1 → E^r_pq surjektiv.
  Die Exaktheit von (i^(r),j^(r)) besagt, dass E^r_pq gerade der Kokern der Abbildung i : D^r → D^r ist.

  Dies zeigt:

  Erpq = ir-1(Dpq) / ir(Dp+1,q-1).

  und demnach gilt:

  Erpq ist isomorph (unter der Abbildung ir-1) zu Dpq / Bild(i)+Kern(ir-1).

  (Wird unter der Abbildung i^r-1 ein Element x auf ein Element i^r(x') in i^r(D_p+1,q-1) abgebildet, so ist i^r-1() = 0, also ist x = i(x') + x - i(x') in Bild(i)+Kern(i^r-1)...)
  Die folgende Skizze zeigt, um welche Abbildungen i und i^r-1 es sich handelt:
  
• Entsprechend sieht man:

  Er+1pq = ir(Dpq) / ir+1(Dp+1,q-1).

  also gilt:

  Er+1pq isomorph (unter der Abbildung ir) zu Dpq / Bild(i)+Kern(ir).

  Und die kanonische Abbildung E^r_pq → E^r+1_pq ist gerade die kanonische Abbildung D_pq / Bild(i)+Kern(i^r-1) → D_pq / Bild(i)+Kern(i^r)

• Also gilt:

  E∞pq ist nichts anderes als Dpq / Bild(i)+(∪Kern(ir)).

Jeder Komplex mit Filtrierung liefert ein exaktes Paar

Beweis: Jede Inklusion F^p-1C_• ⊆ F^pC_• liefert eine lange exakte Homologie-Folge

				...	→
Hn(Fp-1C•)	→	Hn(FpC•)	→	Hn(FpC•,Fp-1C•)	→
Hn-1(Fp-1C•)	→	...

also eine exakte Folge (mit n = p+q):

				...	→
Dp-1,q+1	→	Dpq	→	Epq	→
Dp-1,q	→	...

Dies ist gerade, was wir brauchen!

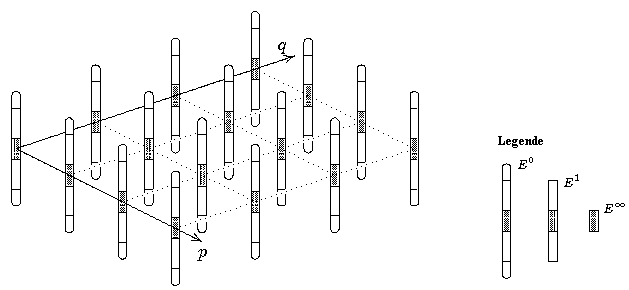
Man sollte sich das Zusammenspiel der verschiedenen langen exakten Homologie-Folgen zu einem exakten Paar folgendermaßen veranschaulichen (dabei schreiben wir X_p statt F^pC_•, entsprechend der Hauptanwendung - der Betrachtung eines toplogischen Raums X mit einer Filtrierung X_p durch Unterräume...):

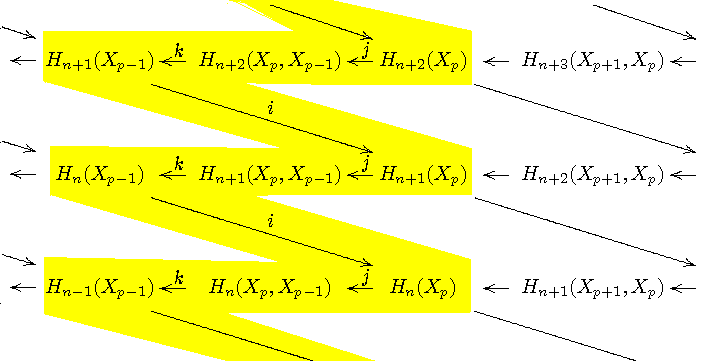
(In der Literatur werden die Abbildungen i oft vertikal gezeichnet, es ergibt sich dann ein "Treppenstufen-Diagramm" (staircase diagram), das sieht vielleicht schöner aus, aber die Position der Gruppen E¹_pq = H_p+q(X_p) entspricht nicht derjenigen im ersten Blatt der zugehörigen Spektralfolge, siehe etwa Spanier, p.472, oder Hatcher.)

Das erste Blatt (E¹,d¹) der zugehörigen Spektralfolge zeigt die relativen Homologie-Gruppen E¹_pq = H_p+q(X_p,X_p-1) und die Abbildungen d = jk (sie verlaufen horizontal zwischen den Gruppen E¹_pq).


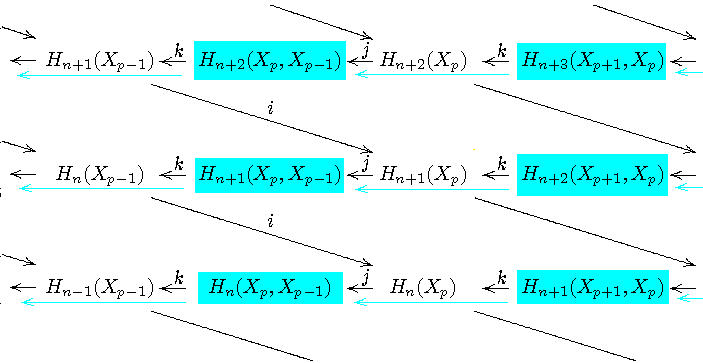
Arbeitet man mit der Spektralfolge, so geht man davon aus, dass die relativen Homologiegruppen E¹_pq = H_p+q(X_p,X_p-1) (und Subquotienten dieser Gruppen) gegeben sind, nicht jedoch absolute Homologiegruppen H_p+q(X_p).