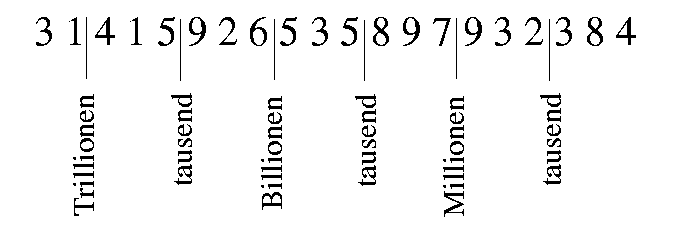
| 1. Die Arithmetik oder Rechenkunst ist eine Wissenschaft, welche uns die Natur und die Eigenschaften der Zahlen lehret, und zugleich einige Regeln an die Hand gibt, vermittelst welcher man die meisten in dem gemeinen Leben vorkommenden Aufgaben ausrechnen oder auflösen kann. |
Die Arithmetik oder Rechenkunst, welche allhier soll abgehandelt werden, ist ein Theil der Mathematik; weswegen zu grösserer Erläuterung dienen wird, mit wenigem zu berühren, worinn diese Wissenschaft bestehet. Die Mathematik ist demnach eine Wissenschaft, welche lehret, wie man aus bekannten Grössen andere, so noch nicht bekannt sind, finden soll. Dasjenige nun, davon in der Mathematik gehandelt wird, ist alles dasjenige, davon die Grösse entweder bekannt ist oder gesuchet wird. Wenn man auch alle Theile der Mathematik betrachtet, so wird man befinden, dass die Sache immer dahin gehe, wie eine unbekannte Grösse aus anderen schon bekannten Grössen soll gefunden werden. Die verschiedenen Theile der Mathematik aber entstehen von den verschiedenen Gattungen der Grössen, indem ein jeder nur eine besondere Art derselben betrachtet. Eine besondere Art der Grössen sind nun die Zahlen, und die Arithmetik [ist] derjenige Theil der Mathematik, welcher mit den Zahlen umgeht. Man kann demnach auch sagen, dass die Arithmetik eine Wissenschaft sei, welche lehret, wie man aus bekannten oder gegebenen Zahlen eine noch unbekannte Zahl finden soll; wie wir dann sehen, dass in allen arithmetischen Operationen allezeit eine Zahl gefunden wird, die vorher unbekannt gewesen. Wie aber die Arithmetik insgemein pflegt traktirt zu werden, so begreift dieselbe noch mehr Operationen und Regeln in sich, als bloss aus der Natur und Beschaffenheit der Zahlen können hergeleitet werden. Man pflegt nämlich mit der eigentlichen Arithmetik noch einige Regeln, welche in der allgemeinen Analysi oder Algebra ihren Grund haben, zu vereinigen, damit ein Mensch, welcher dieselbe erlernet, auch im Stande sei, die meisten Aufgaben, so in dem gemeinen Leben vorzufallen pflegen, aufzulösen, ohne in der Algebra geübet zu sein. Ob demnach gleich diese Regeln zu der Wissenschaft der Zahlen nicht gehören, so ist um angeführter Ursache willen dennoch nöthig, dieselben damit vereinigt zu behalten. Und deswegen haben wir im Anfang vorausgesetzet, dass die Arithmetik ausser der Betrachtung der Zahlen einige Regeln an die Hand gebe, wodurch die meisten in dem gewöhnlichen Handel und Wandel vorfallenden Rechnungen können bewerkstelliget werden.
| 2. Die Arithmetik wird also am füglichsten in zwei Theile getheilet, davon der erste alles dasjenige in sich begreift, was bloss allein in der Natur der Zahlen gegründet ist. Der andere Theil aber enthält diejenigen Regeln, welche bei den meisten Fällen, so in dem gemeinen Leben vorkommen, mit Nutzen angebracht werden können. |
Der erste Theil ist, wie schon gemeldet, die Arithmetik an und für sich selbst, als dessen Grund allein aus der Natur und Eigenschaften der Zahlen fliesset. Und dahin gehören die so genannten Species theils mit ganzen, theils mit gebrochenen Zahlen, indem dieselben ganz und gar auf der Natur der Zahlen beruhen. Ob aber gleich diese Species oder Operationen in allen Rechnungen Platz finden, und auch die schwersten Rechnungen durch diese Operationen ganz allein ausgeführet werden; so sind dieselben dennoch nur als der Werkzeug anzusehen, dadurch dergleichen Rechnungen bewerkstelliget werden. Hingegen ist in solchen Fällen das führnehmste, dass man wisse, welcher Operationen man sich bei einer jeglichen Gelegenheit bedienen müsse, damit das Verlangte gefunden werde. Es ist nämlich nicht genug, die gedachten arithmetischen Operationen zu verstehen, sondern man muss für einen jeglichen Fall eine Regel wissen, welche lehret, was für Operationen gebraucht werden müssen, um dasjenige, was zu wissen verlangt wird, zu finden. Diese Regeln haben nun ihren Grund nicht in der Arithmetik; sondern sind aus der allgemeinen Analysi oder Algebra gelehnet; als wo für eine jede Art von Aufgaben aus den Umständen sonderbare Regeln hergeleitet werden, durch welcher Hülfe man zu richtiger Auflösung gelangen kann. Es werden demnach aus der Algebra so viel und solche Regeln in die Rechenkunst angenommen, als zu den gewöhnlichen Vorfällen auszurechnen nöthig sind. Solchergestalt sind in die Arithmetik aufgenommen worden die Regula Detri, Regula Quinque, Regula Alligationis, Regula Falsi etc., als ohne welche ein Rechenmeister, welcher in der Algebra nicht geübet ist, schwerlich fortkommen kann.
| 3. Wenn viel Stücke von einer Art vorhanden sind, so wird diese Vielheit durch eine Zahl angedeutet. Und deswegen verstehet man durch eine Zahl, von wieviel Stücken die Rede ist. |
Da in dem ersten Theile der Rechenkunst die Natur der Zahlen soll untersuchet, und daraus diejenigen Operationen hergeleitet werden, welche zu Vollziehung der im zweiten Theile vorkommenden Regeln nöthig sind; so muss man sich vor allen Dingen einen deutlichen Begriff von den Zahlen zu wege bringen. Dieses geschieht nun am füglichsten durch Betrachtung desjenigen, welches eins genennet wird; indem eine Zahl andeutet, wieviel Stücke von derselben Sorte vorhanden seien. Als wenn man zum Exempel von hundert Rubeln sprechen höret, so verstehet man, dass von demjenigen Ding, welches Rubel genennet wird, hundert Stücke benennet werden, oder die Zahl hundert zeiget an, von wieviel Stücken, deren ein jedes ein Rubel ist, die Rede sei. Was aber die Grösse der Zahlen betrifft, so wird hier vorausgesetzet, dass derjenige, welcher die Arithmetik zu lernen gesinnet ist, von der Grösse einer jeden Zahl einen Begriff habe und die Worte wisse, damit die Zahlen benennet werden. Hiezu ist aber hinlänglich, nur immer die Zahl benennen zu können, welche herauskommt, wenn zu einer gegebenen Zahl noch eins hinzugesetzet wird. Dann auf diese Art wird ein Mensch mit Zahlen so weit fortfahren können, als man verlangt; und wird dabei von der Menge der Stücken, welche eine jede Zahl andeutet, einen deutlichen Begriff erhalten.
| 4. Alle Zahlen, wie gross sie auch sind, pflegen auf eine sehr kurze und bequeme Art durch nachfolgende zehn Characteres oder Zeichen ausgedrücket zu werden: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Davon die Bedeutung eines jeden, wenn derselbe für sich allein betrachtet wird, genugsam bekannt ist, und also keiner weiteren Erklärung bedarf. |
Zu den arithmetischen Operationen ist nicht genug, eine jede Zahl mit ihrem gehörigen Namen entweder zu nennen oder zu schreiben; sondern es wird zu Erleichterung derselben Operationen erfordert, dass die Zahlen durch besondere und bequeme Zeichen oder Characteres angedeutet werden. Dieses kann nun auf vielerlei Arten geschehen, davon die leichteste und einfältigste ist, wenn so viel Punkten oder Striche hintereinander gesetzet werden, als die Zahl bedeutet: als wenn zum Exempel acht auf diese Art geschrieben wird ||||||||. Diese Art aber ist, wenn die Zahlen sehr gross sind, einer grossen Weitläufigkeit und Undeutlichkeit unterworfen; indem erstlich lange Zeit und ein grosser Raum eine grosse Zahl zu schreiben erfordert, und hernach auch, wenn eine solche Zahl geschrieben, sehr schwer fallen würde, die Zahl zu erkennen. Nach der römischen Schreibart wird zwar diese Weitlaufigkeit und Undeutlichkeit etwas verringert, indem anstatt fünf Strichen dieses Zeichen V, anstatt zehn dieses Zeichen X, und so fort, geschrieben wird; allein da diese Art gleichwohl für grosse Zahlen noch ziemlich weitläufig und undeutlich, dabei auch nicht durch feste Regeln genügsam eingeschränket ist, so ist dieselbe nicht bequem, die arithmetischen Operationen darnach einzurichten. Noch mehr Schwierigkeiten sind diejenigen Arten, die Zahlen zu schreiben, unterworfen, in welchen die Buchstaben des Alphabets zu Bedeutung der Zahlen gebraucht werden; gleichwie vormals bei den meisten Völkern geschehen. Vor diesen Arten hat nun die anjetzo fast allenthalben gebräuchliche Art, die Zahlen durch Hülfe der zehn angeführten Zeichen zu schreiben, einen sehr grossen Vorzug, wie mit mehrerem aus folgendem zu ersehen.
| 5. Bei dieser Schreibart der Zahlen behalten die obigen zehn Zeichen nicht allzeit einerlei Bedeutung: sondern um den wahren Werth eines jeden Characters zu finden, muss man auf die Stelle desselben Acht geben. Als auf der ersten Stelle von der Rechten gegen der Linken behält der Character seine natürliche Bedeutung, als wenn er vor sich allein gesetzet wäre. Auf der zweiten Stelle bedeutet ein Character zehnmal mehr als wenn er allein stünde. Auf der dritten Stelle bedeutet ein Character hundertmal mehr, auf der vierten tausendmal mehr, und so fort, immer zehnmal mehr auf der folgenden Stelle, als auf der vorhergehenden. |
Hiebei ist nun zu merken, dass das Zeichen 0 auf allen Stellen nichts bedeutet, weilen zehnmal nichts und hundertmal nichts und so fort allzeit nichts ausmacht. Wie aber die Vermehrung der Bedeutung der übrigen Zeichen nach den Stellen beschaffen sei, so ist zu merken, dass der Werth eines jeglichen Characters zehnmal grösser sei, als auf der vorhergehenden Stelle nach der rechten Hand. Und deswegen hat man sich nachfolgende Tabelle nöthig wohl bekannt zu machen:
|
Aus dieser Tabelle bekommt man also einen Begriff von den Zahlen zehn, hundert, tausend und so fort; indem man daraus sieht, wieviel Stücke eine jede Zahl vorstellt. Hieraus kann man aber ferner abnehmen, wieviel ein jeder Character von den obgedachten zehn in einer jeden Stelle bedeute. Nämlich in der ersten Stelle von der rechten gegen der linken Hand bedeutet wie folget:
| I |
|
|
Auf der zweiten Stelle aber bedeutet
| II |
|
|
Auf der dritten Stelle bedeutet
| III |
|
|
Auf der vierten Stelle bedeutet
| IV |
|
|
Auf der fünften Stelle bedeutet
| V |
|
|
Auf der sechsten Stelle bedeutet
| VI |
|
|
Auf der siebenten Stelle bedeutet
| VII |
|
|
Hieraus erhellt, dass die Bedeutung der Characteren auf der siebenten Stelle ähnlich sei der Bedeutung auf der ersten Stelle, indem bei der siebenten nur das Wort Millionen zugesetzet wird. Gleichergestalt wird man die Bedeutung auf der achten Stelle haben, wenn man bei der zweiten Stelle das Wort Millionen hinzusetzet; und auf eben diese Art entspringt die neunte Stelle aus der dritten, die zehnte aus der vierten, und so weiter bis auf die dreizehnte und folgenden, welche wieder aus der ersten und folgenden durch Beisetzung des Wortes Billionen formirt werden. Endlich bedeuten die Characteres auf der neunzehnten Stelle Trillionen, die auf der fünfundzwanzigsten Quadrillionen und so fort; woraus zugleich die Benennung der mittleren Stellen erhellet. Solchergestalt bedeutet in dieser Zahl 7302568 der Character
|
Woraus also der Werth oder die Bedeutung eines jeglichen Characters in einer auf dieser Art geschriebenen Zahl erkannt wird.
| 6. Die Grösse einer Zahl, welche durch viel hintereinander gesetzte Characteres ausgedrückt wird, findet man, wenn man die Bedeutungen aller Characteres zusammensetzet. Wobei die Gewohnheit mit sich bringt, in Benennung derselben von der Linken zu der Rechten fortzugehen. |
Gleichwie diese Schreibart der Zahlen willkürlich ist, also beruhet auch die Ordnung, nach welcher die Zahlen ausgesprochen werden, auf der Gewohnheit. Wir gehen aber in Benennung der Characteres deswegen hauptsächlich von der Linken zu der Rechten, dieweilen auf diese Art fast eben der Name, welchen eine jegliche Zahl in unserer Sprache führet, herauskommt. Diesemnach werde die obige Zahl 7302568 soviel ausmachen wie folgt: Sieben Millionen, dreihunderttausend und zweitausend und fünfhundert und sechzig und acht. Nach der Eigenschaft unserer Sprache aber wird diese Zahl also ausgesprochen: Sieben Millionen, dreihundertundzweitausend, fünfhundertundachtundsechzig; welche Art von der vorigen nur darinn unterschieden ist, dass, da oben tausend zweimal nacheinander vorkommt, hier nur das letztere Mal gesetzet wird, indem es auf diese Art gesetzet auch zugleich zu dem vorhergehenden gehöret. Überdas sagt man anstatt sechzig und acht, achtundsechzig. Aus welchem allen erhellet, dass diese Art, die Zahlen zu schreiben, mit der gewöhnlichen Art, die Zahlen mit Worten auszusprechen, sehr genau übereinkomme, indem uns eine jegliche Zahl beinahe die gewöhnlichen Worte, und das in eben der Ordnung in den Mund legt; welche Gemeinschaft fast in allen Sprachen, in einer aber mehr als in der anderen, beobachtet wird.
| 7. Um eine jegliche auf diese Art beschriebene Zahl, aus wieviel Characteren dieselbe auch immer bestehet, mit den gehörigen Worten auszusprechen, hat man nur nöthig zu wissen, wie diejenigen Zahlen, welche nur aus dreien Characteren bestehen, ausgesprochen werden; dieses geschieht nun, indem man den ersten Character gegen die linke Hand mit seinem natürlichen Namen nennet und dazu das Wort hundert setzet; hierauf nennet man in der deutschen Sprache den ersten Character gegen der Rechten und setzet dazu den Namen des mittleren, welchen er in der zweiten Stelle, wie oben gesetzet, erhält. |
Wenn die Zahl nur aus zweien Characteren bestehet, oder der erste gegen der linken Hand 0 ist, so werden nur die zwei letzteren ausgesprochen; dann dieser Character 0, welcher nichts bedeutet, wird niemals ausgesprochen. In der deutschen Sprache ist nur einige Schwierigkeit, eine Zahl, so aus zweien Characteren bestehet, auszusprechen, indem die letztere gegen der rechten Hand zuerst genennet wird. Ist aber dieser Character eine 0, so wird nur der erste gegen der linken Hand mit dem Namen, welchen er in der zweiten Stelle hat, benennet. Also ist 10 zehn, 20 zwanzig, 30 dreissig, und so fort. Weiter ist 11 eilf oder eins und zehn, 12 zwölf oder zwei und zehn, 13 dreizehn, 14 vierzehn, und so fort bis auf zwanzig. Von zwanzig aber bis auf hundert geht die Benennung nach der gegebenen Regel, nämlich 27 heisst sieben und zwanzig, 56 heisst sechs und fünfzig, 89 heisst neun und achtzig, und so fort. Hat man nun die Aussprechung zweier Character begriffen, so ist sehr leicht, alle Zahlen, welche mit drei Characteren geschrieben werden, auszusprechen, indem nur erstlich der erste von der Linken nebst Zusetzung des Worts hundert genennet, und die zwei folgenden wie gelehret, mit den Worten hinzugesetzet werden. Also ist 114 hundert und vierzehn, 570 fünfhundert und siebenzig, 324 dreihundert und vierundzwanzig, 208 zweihundert und acht, 600 sechshundert, und so fort.
| 8. Hat man nun gelernet alle Zahlen, so mit dreien oder weniger Characteren geschrieben werden, aussprechen, so ist sehr leicht, alle Zahlen, aus wieviel Characteren sie auch immer bestehen, mit ihren gehörigen Worten auszusprechen. Dieses geschiehet, indem von der rechten Hand anzufangen je drei und drei Characteres abgeschnitten werden, so dass die ganze Zahl in eine gewisse Anzahl Glieder zertheilet wird, deren jedes aus drei Characteren besteht. Ein jedes Glied wird nun mit eben den Worten, als wenn es allein stünde, ausgesprochen, und dazu ausser bei dem ersten von der Rechten gegen der Linken ein besonderes Wort hinzugesetzet; als bei dem zweiten von der Rechten tausend, bei dem dritten Millionen, bei dem vierten tausend, bei dem fünften Billionen und so fort. Auf diese Art wird nun ein Glied nach dem anderen ausgesprochen, der Anfang aber von der Linken gemacht und gegen der Rechten fortgefahren. |
Diese Eintheilung in Glieder, deren jedes drei Characteres enthält, geschiehet von der Rechten gegen der Linken, so lang Characteres vorhanden; weswegen zu merken, dass das letzte Glied nicht allezeit aus drei Characteren bestehe, sondern vielmal nur zwei oder einen enthalte; da aber gleichwohl dieselben, als wenn sie allein stünden, ausgesprochen werden mit Hinzusetzung des gehörigen Worts. Was nun diese Wörter betrifft, so sieht man, dass von der rechten gegen der linken Hand diese Glieder, nämlich: das zweite, vierte, sechste, achte, zehnte und so fort, alle das Wort tausend mit sich führen. Das dritte aber hat bei sich das Wort Millionen, das fünfte Billionen, das siebente Trillionen, das neunte Quadrillionen, und so fort. Eine jede vorgegebene Zahl kann also auf folgende Art zur Aussprechung zugerüstet werden:
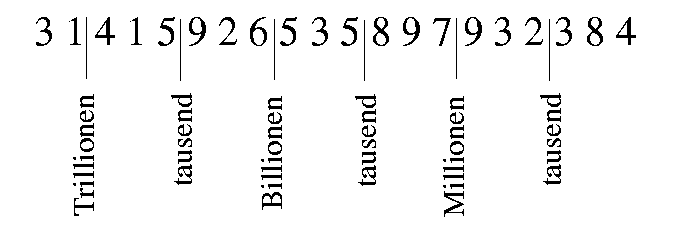
oder auch anstatt der Worte nur Zeichen wie folget:
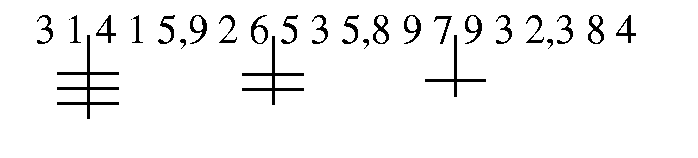
allwo die Commata anstatt tausend stehen, die Zeichen
Diese Zahl wird nun also ausgesprochen: Zehn Quadrillionen,
zweihunderttausend und dreihundert Trillionen, vierzigtausend
Billionen, fünfhunderttausend und sechs Millionen, neuntausend und
sieben. Auf diese Art wird nun eine jede Zahl, welche mit diesen
Characteren beschrieben ist, erkannt und mit Worten ausgesprochen. Nun
folget, wie eine jede Zahl, welche mit Worten ausgesprochen wird,
durch diese Characteres auf gemeldete Art geschrieben werden
soll. Dieses aber desto besser vorzutragen, ist nöthig, vorher einige
Wörter zu erklären.
Dieses deutlicher vor Augen zu legen dienet folgende Tabelle,
welche weiset, was die Characteres auf einer jeglichen Stelle für
eine Bedeutung haben: als
Hiebei ist nun zu merken, dass eine Decas zehn Unitäten oder
einzele Stücke enthalte, ein Centenarius aber zehn Decades, ein
Millenarius zehn Centenarios, eine Decas millenariorum zehn
Millenarios und so weiter.
Wenn man sich also einen Begriff von diesen Worten gemacht, so
siehet man gleich, wieviel Stücke eine jegliche Zahl von einer
jeglichen Sorte enthalte; als diese Zahl 5 738 264 enthält: 5
Millionen, 7 Centenarios millenariorum, 3 Decades Millenariorum, 8
Millenarios, 2 Centenarios, 6 Decades und 4 einzele oder
Unitates. Hievon aber einen deutlichen Begriff zu geben, so lasset uns
setzen, ein Mann habe in seinem Vermögen so viel Rubel, als diese
Zahl 5 738 964 ausweiset. Die Grösse dieses Vermögens wird
nun am deutlichsten erkannt, wenn man sagt, dieser Mann habe erstlich
5 Kisten, in deren jeder eine Million Rubel sei; und dann noch 7
Kisten, jede von hunderttausend Rubel; drittens 3 Kisten, jede von
zehntausend Rubel; viertens 8 Säcke, jeden von tausend Rubel;
fünftens 2 Säcke, jeden von hundert Rubel; sechstens 6
Beutel, in deren jedem zehn Rubel; und endlich noch dazu 4 einzele
Rubel. Aus einer solchen Beschreibung wird nun ein jeder von diesem
Reichthum einen deutlichen Begriff bekommen; und wenn wir recht
nachdenken, so werden wir befinden, dass sich ein jeder eine grosse
Zahl auf eben diese Art vorstellet. Dann was wir dorten Unitäten
genennet, sind in diesem Exempel einzele Rubel. Eine Decas ist hier
ein Beutel von zehn Rubel. Ein Centenarius ist hier ein Sack von
hundert Rubel und so fort.
Wenn also nach dieser Art sollte geschrieben werden
zweihundertundsechstausend, siebenhundertundfünfzig; so hat man
zu sehen, dass erstlich 2 Centenarii millenariorum vorhanden, welche
auf die sechste Stelle gehören; hernach sind 6 Millenarii da auf
die vierte Stelle, und dann 7 Centenarii auf die dritte Stelle, und
endlich 5 Decades auf die zweite Stelle; so dass also die fünfte
und die erste Stelle ledig bleiben. Diese Zahl wird demnach in unseren
Characteren also stehen 206 750. Wer sich aber in Aussprechung der
Zahlen, wie vorher gelehret worden, einigermassen geübet, wird
zugleich im Stande sein, eine Zahl, welche er gehöret
aussprechen, wiederum zu schreiben: und wenn es auch nicht recht
gerathen sollte, würde er den Fehler bald merken, wenn er seine
geschriebene Zahl wiederum mit Worten ausdrücken sollte. Hiebei
aber kann man dennoch einige Regeln geben, dass man in diesem Werke um
so viel sicherer verfahre. Wenn die Zahl, wie es die Gewohnheit mit
sich bringt, so ausgesprochen wird, dass erstlich die grössten
Sorten und denn der Ordnung nach die kleineren benennet werden, so
kann er gleich von der Linken gegen der Rechten die Characteres einer
jeglichen Sorte schreiben, wenn er merket, dass von allen nach der
höchsten folgenden Sorten etwas vorhanden ist. Trifft sich aber,
dass eine oder einige Sorten nicht benennet wurden, so kann er
dieselben auch gleich merken und die Stellen derselben mit 0
ausfüllen. Das fürnehmste hierinn ist, dass man die Zahlen,
welche kleiner sind als tausend, wohl wisse zu schreiben und auf ihre
gehörigen drei Stellen zu setzen, denn sowohl die Tausender als
Millionen, Billionen etc. durch solche Zahlen gezählet zu werden
pflegen. Hernach ist auch zu beobachten, dass die Millionen,
Billionen, Trillionen etc. sechs Stellen in ihrem Bezirk haben; denn
dann eine jegliche Art insbesondere kann geschrieben werden: wobei nur
zu merken, dass nach den Millionen gegen der Rechten noch 6 Stellen,
nach den Billionen zwölf Stellen, und so fort, folgen
müssen. Endlich ist auch zu merken, dass niemals von einer Sorte
mehr als neun können geschrieben werden, indem 10 Stücke von
einer Sorte ein Stück von der folgenden ausmachen und folglich
dahin gehören. Deswegen muss sich einer nicht verführen
lassen, wenn man ihm zu schreiben vorlegt eilftausend, eilfhundert und
eilf; er muss nämlich wissen, dass eilfhundert einen Millenarium
nebst einem Centenario ausmache und deswegen wird er haben
zwölftausend einhundert und eilf, welche also geschrieben werden
12111.
Es ist willkürlich, was für Character zu Beschreibung
der Zahlen gebrauchet werden; eine jede Art aber der Zahlen
auszudrücken, erfordert besondere Regeln zu den arithmetischen
Operationen, welche aus der Beschaffenheit einer jeglichen Art
müssen hergeleitet werden. Wir haben aber bisher genugsam
dargethan, dass die gewöhnliche Art vermittelst der zehn
Character am allerbesten mit den Worten, dadurch die Zahlen benennet
werden, übereinkommen; wie es dann auf diese Art sehr leicht ist,
eine jede durch solche Characteres beschriebene Zahl mit Worten
auszusprechen, und hinwiederum eine mit Worten benennte Zahl zu
schreiben. Da nun die arithmetischen Operationen nach dieser Art am
bequemsten eingerichtet worden, so war, ehe man zu den Operationen
selbst schreiten konnte, unumgänglich nöthig, diese
Ausdruckungsart der Zahlen ausführlich zu erklären, damit
daraus die Regeln für die Operationen konnten hergeleitet
werden. Diese Vorbereitung zu den arithmetischen Operationen wird nun
Numeratio oder Notatio genennet, welche lehret eine jegliche Zahl
schreiben, und wenn eine Zahl geschrieben, wiederurn aussprechen. Die
Numeration kann also nicht mit unter die Operationen gezählet
werden, wenn wir durch eine Operation eine besondere Art verstehen,
aus zweien oder mehr gegebenen Zahlen eine neue herauszubringen. Da
wir nun durch Ausführung der Numeration das Fundament zu den
arithmetischen Operationen geleget, daraus dieselben gründlich
können erkläret werden, so schreiten wir zu diesen
Operationen selbst fort, wenn einige Exempel zur Übung werden
beigebracht sein.
Antw.: fünftausendvierhundert deutsche Meilen.
Antw.: dreizehntausend sechshundertfünfundneunzig Millionen,
dreihundertundachtzigtausend und fünfzig Kronen.
Antw.: eine Million und zweimalhunderttausend Kronen, oder auch
zwölfmalhunderttausend Kronen.
Antw.: hundertundfünfundvierzigtausend Millionen Goldgulden.
Antw.: eintausend Octillionen. Nämlich die letzteren achtundvierzig
Cyphren geben Octillionen, und vor denselben stehet noch 1000, das ist
tausend.
Antw.: zwölf Trillionen, dreihundertundfünfundvierzigtausend
sechshundertundachtundsiebenzig Billionen, neunhunderttausend
neunhundertundsiebenundachtzig Millionen
sechshundertundvierundfünfzigtausend dreihundertundeinundzwanzig.
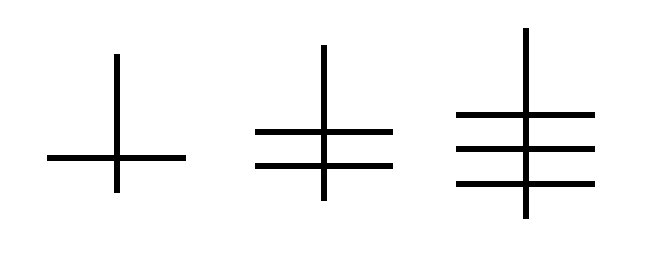
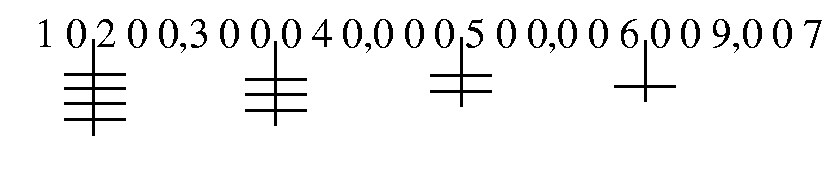
9. In einer nach obgemeldter Art beschriebenen Zahl stehen auf der
ersten Stelle von der Rechten gegen der Linken die Unitäten, weilen
der auf dieser Stelle stehende Character anzeiget, wieviel einzele
Stücke vorhanden sind. Auf der zweiten Stelle sind die Decades, indem
der Character auf dieser Stelle ausweiset, wievielmal zehn einzele
Stücke vorhanden. Ferner werden die auf der dritten Stelle Centenarii
genennet, auf der vierten Millenarii, auf der fünften Decades
millenariorum, auf der sechsten Centenarii millenariorum und auf der
siebenten Milliones. Wenn man nun die Millionen als einzele Stücke
betrachtet, so befinden sich auf der achten Stelle wieder Decades,
nämlich Millionum, auf der neunten Centenarii und so wiederum fort
bis auf Billionen auf der dreizehnten Stelle. In gleicher Ordnung geht
man wiederum fort bis auf Trillionen und so weiter.
Stellen
die Bedeutung
1
Unitates
2
Decades
3
Centenarii
Unitatum
4
Millenarii
5
Decades millenariorum
6
Centenarii millenariorum
7
Unitates
8
Decades
9
Centenarii
Millionum
10
Millenarii
11
Decades millenariorum
12
Centenarii millenariorum
13
Unitates
14
Decades
15
Centenarii
Billionum
16
Millenarii
17
Decades millenariorum
18
Centenarii millenariorum
19
Unitates
20
Decades
21
Centenarii
Trillionium
22
Millenarii
23
Decades millenariorum
24
Centenarii millenariorum
10. Um eine Zahl, welche ist vorgegeben worden, zu schreiben, muss
man erstlich sehen, wieviel dieselbe von einer jeglichen Sorte aus der
vorigen Tabelle enthalte. Hernach wenn dieses geschehen, muss die
Anzahl einer jeglichen Sorte auf die in eben der Tabelle angezeigte
Stelle gesetzet werden. Wo aber, nachdem dieses alles geschehen, noch
einige Stellen ledig bleiben, müssen dieselben mit dem nichts
bedeutenden Character 0 erfüllet werden. Weswegen also hiezu dienlich
ist, die Stellen, wenn man weiss wieviel derselben vorhanden sein
müssen, mit Punkten zu bemerken.
11. Dasjenige, welches bisher ist erkläret worden,
nämlich wie man eine durch Characteres beschriebene Zahl mit
Worten aussprechen und hinwiederum eine jede Zahl durch solche
Characteres schreiben soll, wird die Numeration genennet und pflegt
gemeiniglich für die erste arithmetische Operation gehalten zu
werden.
Exempel der Numeration
![]() ; wie muss nun diese Zahl mit Worten
ausgesprochen werden?
; wie muss nun diese Zahl mit Worten
ausgesprochen werden?