SFB 343
Zum SFB 343 ist im der der Festschrift zum 25-jährigen Bestehen der Universität ein Artikel von Prof. Dr. Bernd Fischer erschienen. Es liegen weiterhin der Forschungsantrag für Teilprojekt C1 (3 MB) von Prof. Fischer und der Allgemeine Teil (23 MB) des letzten Arbeitsberichts als pdf-Dateien vor.
Des weiteren hielt Prof. Dr. Claus-Michael Ringel, einer der Sprecher des SFB 343, beim Festakt zum 50-jährigen Bestehen der Fakultät einen Vortrag über diesen Sonderforschungsbereich:
Discrete Structures in Mathematics
The SFB 343 (1989 - 2000)
Bielefeld University was founded in 1969. Mathematics was one of the first, and also one of the largest departments (all were called faculties).
Bielefeld University was established as a research university. Schelsky, a German sociologist, had been asked to create a university according to his concepts. He focused on sociology (of course), but second also on mathematics: he was aware of the importance of mathematics (quite astonishing in Germany, nowadays). Sociology and mathematics were the two relevant pillars of Bielefeld University. Around sociology, Schelsky grouped history and law, literature, psychology and pedagogy, around mathematics physics, chemistry, biology and economics, but also an additional research unit on mathematization. And there was the special rule for professors: to teach only every second year, a privilege which unfortunately was soon abandoned!
Mathematics was designed as a rather large department, but then, year by year, it lost positions, one after the other, based on the calculation of the teaching capacity by the state (North Rhine-Westphalia). The policy of the state was to support teaching, not research, but there was the possibility to apply for a special research unit (this is the meaning of the letters SFB, the official translation is Collaborative Research Centre, abbreviated CRC). Such an SFB is jointly financed by the DFG (the central research funding organization in Germany) and the state.
1. What is an SFB?
An SFB (CRC) is a research unit for a limited number of years, with a definite aim, for example to construct an engine. You apply for support say for 12 years; there are 3 well-defined periods, the first one to make an outline, the second to produce a prototype, the third one to finish the development so that the product is ready for the market: it should be research for a fixed period, with a definite goal, a definite end!
Mathematical research does not fit into such a scheme - important problems may be partly solved, but one cannot expect a clear cut end. Thus, there was common agreement that SFBs are not suitable for mathematics. There was an exception, the Bonn SFB, established for Hirzebruch, an appraisal for Hirzebruch, but a curiosity for the research council. Hirzebruch's intention was to establish a guest program, like at Princeton, something very strange for Germany, if your guideline for an SFB is the construction of an engine. But many years later, the research council suggested this kind of guest program (and the relevance of international contacts) to all the SFBs, referring to the positive experience in Mathematics and Physics.
Most SFBs are centered around a single person (being then the Speaker of the SFB). Usually this is a prominent scholar, and the SFB is established to support his or her research. The Bielefeld SFB was quite different, with several very prominent mathematicians as members, and with a Speaker being considered may-be as primus inter pares, or just as a clerk.
SFBs are numbered consecutively, the Bielefeld SFB Discrete Structures in Mathematics had the number 343. It started on July 1, 1989 (with an inauguration ceremony on October 18) and ended by the end of 2000.
| 343 = 7×7×7 |  |
There is what Borho calls the Heisenberg Uncertainty Principle of research support in Germany: there always had been two main schemes of support, one concerns fixed topics, but is locally widespread, these are the Priority Programmes. The other one, the SFBs, are devoted to a fixed locus, but here a broad collection of topics is allowed. Actually, there was a small problem with the Bielefeld SFB: Waldhausen insisted that topologists from Osnabrück were included. This was difficult, since Osnabrück does not even belong to North Rhine-Westphalia (and the funding is partly by the state). Thus, the first application was vague about the inclusion of Osnabrück and avoided the discussion: Osnabrück was added only after the inauguration.
2. The end.
Let me jump to the end of the SFB. As I mentioned, an SFB cannot go indefinitely, there always has to be an end. The SFB 343 ended in 2000, but it could have lasted for another 3 years (nowadays, 12 years is the usual limit). When the end of the SFB was discussed, I was Speaker of the SFB. There was a vehement fight by me for a continuation. A fight which I lost. Even Ahlswede praised very highly my commitment (usually, he criticized whatever I did). I wanted to resign, but that may have damaged the last research period, thus I was afraid to do so.

There was an intermission between the end of this SFB in 2000 and the begin of a new SFB in 2005. Such a disruption is very bad, since infrastructure gets lost! One of the main problems of running an SFB with a big guest program are the arrangements for the visitors, in particular to find suitable accommodation: you need contact to many landlords and conversely, they want to rely on a stable contact.
What were the reasons for the termination? The panel of referees was afraid that an end of the SFB in 2003 would coincide with the generation change: as you know, the retiring age in Germany is 65, and many mathematicians involved in the SFB were born in the period 1936-1942: Ahlswede, Fischer, Dress, Detlef Voigt, Waldhausen, Elsner, Abels, Deuber (as Dress has pointed out, especially the year 1938 was a really good vintage, maybe not for red wine, but for becoming a math professor in Germany). The panel wanted to watch the hiring policy of Bielefeld. There was the promise that there could be a new SFB provided that the Bielefeld hiring policy deserved it. Apparently it did: the new SFB was established in 2005.
The weeks before the meeting, I traveled to Bonn, to Freiburg, I spoke with the DFG, with some of the referees, for example with Soergel. So I found out that a continuation would be difficult to get. But I was not aware that DFG-decisions are usually completely predetermined.
3. The start.
Here is the Bielefeld crew which started the SFB:
| The start of the SFB (1989) |
 |
(with Genius from the DFG, and with Grotemeyer, the rector of Bielefeld University). The middle picture is from a local newspaper. Since two of the project leaders are missing (Abels and Götze), they are added on the left and on the right. All the pictures are from 1989.
Already in 1985, there were preconsiderations. Dress was a strong promoter, but he did not want to become the Speaker. His suggestion was Deuber.
The first discussions with the research council, say with Dr. Paul Roberts Königs (who was responsible for mathematics at that time and who himself had a very clear vision about possible developments), showed that the DFG as well as the state of North Rhine-Westphalia were inclined to have a new SFB, but that the preference was definitely Münster. Only when Münster did not show any interest, was Bielefeld was seriously considered. (Later, when a new generation of mathematicians at Münster decided to apply for an SFB, they were sure that this would be a replacement, not an addition: Schneider was very surprised that Bielefeld dared to apply for a continuation parallel to the application of Münster).
One should be aware that there is not just the application. What is really important is a pre-application. One gets some advice on how to improve the application. This is just an advice, without any legal standing. But either you follow it, or else you can just forget the application. Decisions of the DFG are usually predetermined.
The Bielefeld mathematics faculty was sometimes nicknamed a faculty of group theory. In principle, the SFB followed the structure of mathematics in Bielefeld, thus, the SFB was in some sense an SFB for group theory. There were fights about participation: Hallstein doctrines were formulated: that X would never join an SFB, if Y will be a member. Leptin told me later that he did not expect an SFB, as designed, would be approved, so he decided not to participate. Another mathematician threatened to go to court if he was not incorporated ...
A big task for an application is to present a concise research project, outlining the present state of the art and formulating open questions which will be solved. This is dangerous, because in mathematics you never know whether you can solve a problem or not. Here is Deuber's principle for successful research applications: To mention only problems which you already have solved, but not yet published.
In 1991, the first prolongation was due. Ahlswede was annoyed at again having to formulate a research program - he refused to do so and just copied the 1989 text. When the referees arrived, he became aware that they were furious. Thus, over night, he wrote several new pages. Even Ahlswede had to realize that it is important to please the referees.
The godfathers. There were two godfathers, both from Bonn (the mathematical center at that time, of course also nowadays): Hirzebruch and Korte.
 |
 |
| Hirzebruch | Korte |
Of course, parts of the SFB were related to the interests of Hirzebruch, parts to those of Korte (already the title Discrete structures refers to the expertise of Korte). But it was also advisable, not to have too much overlap with existing or already planned research activities in Germany.
Korte: For a decisive meeting, he claimed to be ill, but letting everyone know that it was a political illness (related to rumors about a PhD at Bielefeld) and clearly he was sure that his absence would kill the application - but it didn't.
Hirzebruch: You know: Christians venerate God as a trinity: The Father, the Son (Jesus), and the Holy Ghost. God in three persons, threefold. When Hirzebruch came to a meeting, he usually came in four persons, fourfold.
 |
Say, at a round table, they were distributed well in four possible directions, and Hirzebruch needed only small twinkles to orchestrate their contributions. At the beginning, these were Hirzebruch, as well as Tits, Harder, and Scharlau, Harder was always present, he monitored (with Soergel) the final destruction of the SFB. Tits was present only at the beginning, later Kreck was substituted.
4. The shape of the SFB.
The SFB consisted of three parts, labeled A, B, C. Here are the projects (the titles are shortened):
| A | Simplicial Methods | ||
|---|---|---|---|
| A1 | Vogt/Waldhausen | Algebraic K-Theory of Top Spaces | |
| A2 | Abels | Finiteness Conditions for Groups | |
| A3 | Mennicke | Combinatorial Group Theory | |
| A4 | Dress | Tesselations | |
| B | Discrete Models | ||
| B1 | Ahlswede | Sequence Spaces | |
| B2 | Ahlswede | Information Exchange | |
| B3 | Götze | Discrete Non-parametric Models | |
| B4 | Deuber | Combinatorics | |
| B5 | Dress | Matroids | |
| B6 | Elsner | Eigenvalue Problems for Matrices | |
| C | Discrete Methods in Algebra | ||
| C1 | Fischer | Finite Simple Groups | |
| C2 | Ringel | Representations of Algebras | |
You may wonder (as I always did) about the logic behind the separation A-B-C. The parts A and C seem to fit perfectly together, but they are separated by B (the applied topics). B looks like a bumper between A and C. But it was used also as a pretense: that the applied mathematics is the center, surrounded by pure (or poor) mathematics.
Cooperations, Unity of mathematics. There was the question of cooperation between the different parts. So Deuber, coming from graph theory, proposed to draw a graph to outline related projects. A week later, he presented the following graph:
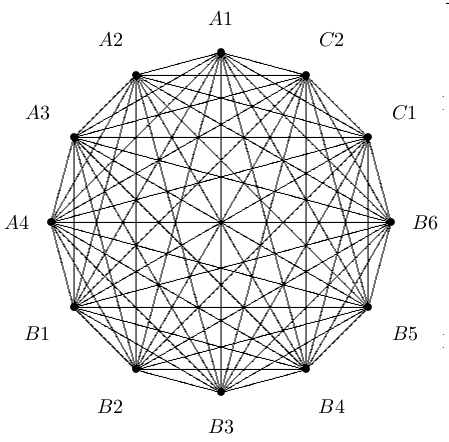
He just was drawing the complete graph with 12 vertices. It is a nice picture, but completely meaningless. A later version (in the application handed in to the DFG) looks as follows:
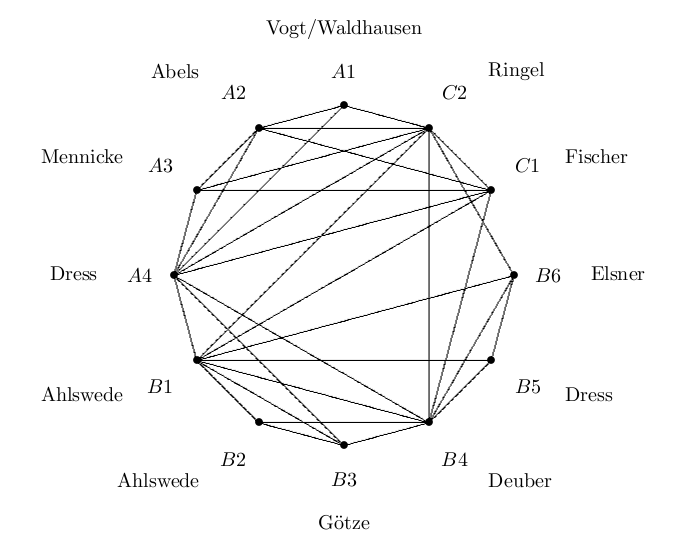
Note that the cyclic arrangement hides the fact that B is a bumper between A and C. But still you can observe that most of the connections are, on the one hand, in the upper part, within A and C, and, on the other hand, in the lower part, inside B.
Some of the projects are quite isolated. In particular, and this may be astonishing, this applies to the project B5 of Dress, devoted to matroids. Matroids are definitely a basic discrete structure, and could be relevant in many different settings, say for all topics which deal with linear algebra problems. As I mentioned, Korte was one of the godfathers of the SFB, and his main concern was always matroids. But as you see, when Bielefeld applied for the SFB, it was not even pretended that matroids could be considered as a universal device.
However, linear algebra methods themselves have to be seen as a common theme of the SFB, this concerns the character tables for groups handled by Fischer (C1), the representation theory of algebras in project C2, the numerical linear algebra considered by Elsner in B6, the study of Linear Groups in A2. (Actually, there were many parallel developments in projects B6 and C2: the interest in Kronecker's classification of matrix pencils, the deformation theory for matrix pencils, or, equivalently, for Kronecker modules, the study of vector spaces over the quaternions.) Also, Deuber's interest in Ramsey theory was devoted to vector spaces and finite abelian groups: to extend the usual set theoretical setting to an algebraic one.
Concerning possible cooperations and the unity of mathematics, let me quote from the first Bewilligungsbescheid, the first official "Notification of Approval" by the DFG: The connections between the projects of the Pure and of the Applied Mathematic need altogether to be improved. At the moment there is a lack of symmetry in as far as the Applied Mathematicians in Part B tend to ignore the mathematical problems which turn up in Parts A and C. A very amazing assessment! The Applied Mathematicians are criticized for ignoring problems in Pure Mathematics. This rating is also formulated in an advice for Project B1: In Project C2 as well as in other Projects of the SFB combinatorial problems arise which could be attacked in cooperation with Mr Ahlswede. We expect his collaboration on these problems and hope that in this way he supports the endeavor.
(The exact formulations are: Zu dem Sonderforschungsbereich insgesamt ist folgendes zu sagen. 1. Die Kohärenz des Forschungs-Programms erscheint für die Anfangsphase zufriedenstellend. Vor allem die Projektbereiche A und C sind bereits jetzt hinreichend miteinander verbunden. In sich inhaltlich geschlossen stellt sich auch der Projektbereich B dar. Die Verbindungen zwischen dem Projekten aus der Reinen und der Angewandten Mathematik sind allerdings insgesamt verbesserungsbedürftig. Derzeit besteht ein Mangel an Symmetrie insofern, als die Angewandten Mathematiker im Projektbereich B die in den Projektbereichen A und C anfallenden Fragen nur begrenzt aufgreifen. In Zukunft wird ein stärkeres Eingehen von dieser Seite auf die in den Projektberichen A und C anfallenden Problemen erwartet. ... (page 13). Hinweis zum Teilprojekt B1 Kombinatorik von Folgenräumen (Ahlswede): Im Teilprojekt C2 und auch in anderen Teilprojekten des Sonderforschungsbereichs treten kombinatorische Fragen auf, für die sich Herr Ahlswede als Kooperationspartner anbietet. Es wird erwartet, dass er an Fragestellungen dieser Art mitarbeitet und damit die genannten Vorhaben unterstützt. (page 11))
Later changes. The projects A4, B5 by Dress ended in 1992 (or, better, they were incorporated into a University Institute for Structure Formation Processes), the project C1 by Fischer ended in 1994. After the retirement of Mennicke in 1996, the project A3 was continued by Helling. Also, some projects were renamed (in particular, the project A2 of Abels) or expanded their scope. Here is the list of the projects when the SFB ended (essential changes are marked in yellow):
| A | Simplicial Methods | ||
|---|---|---|---|
| A1 | Vogt/Waldhausen | Algebraic K-Theory of Top Spaces | |
| A2 | Abels | Linear Algebraic Groups | |
| A3 | Helling | Combinatorial Group Theory | |
| B | Discrete Models | ||
| B1 | Ahlswede | Sequence Spaces | |
| B2 | Ahlswede | Information Exchange | |
| B3 | Götze | Discrete Non-parametric Models | |
| B4 | Deuber | Combinatorics | |
| B6 | Elsner | Eigenvalue Problems for Matrices | |
| B7 | Röckner | Dirichlet Forms | |
| C | Algebraic and Geometric Methods | ||
| C2 | Ringel | Representations of Algebras | |
| C3 | Zink | Schimura Varieties | |
| C4 | Bauer | 4-dim Manifolds | |
| C5 | Ringel | Quantum Groups | |
As you see, part C which was named before Discrete Methods in Algebra, now got the name Algebraic and Geometric Methods and their Applications - this reflects a decisive change, but was accepted without any discussion by the research council and by all the referees. (Remark. Let me add here an appraisal of the DFG and its referees. They look very carefull at all applications as well as at all reports. Dealing with applications and reports, they spot phony words and fake arguments, but fortunately, they usually do not compare reports with the corresponding applications, knowing that mathematical research does not follow timetables. I have to admit that there have been some sad exceptions, in particular one in the second Bielefeld SFB, but this seems to occur rarely.)
There were 4 new projects, the projects B7, C3, C4 and C5; mainly related to the hiring of new faculty members. In this way, the parts B and C were expanded.
First of all, in part B, Röckner's project on Dirichlet forms started in 1994.
The project C3 by Zink started already in 1992. A decisive reason for hiring Zink was the hope to foster the cooperation between information theory (Ahlswede) and say algebra and geometry, to build a bridge between the projects B1 and B2 of Ahlswede and part C of the SFB. As you may know, Ahlswede was recipient of an IEEE award (even twice), as was Zink (for his joint work in 1982 with Tsfasman and Vladut on non-linear codes), thus coding theory could have become a future highlight of the SFB. The first impetus came from Rapoport signalizing that Zink would be available as a candidate and the idea was strongly favored by some of the SFB-referees (but not at all by all members of the SFB). In such a situation, there usually was a strong bias between A on the one hand, and B and C on the other hand whether to promote the unity of mathematics or not ...
Finally, the project C4 by Bauer started in 1994. Let me stress that also the hiring of Bauer was initiated and forced by Ahlswede, after contacts with Kreck (and again with a lot of opposition inside the faculty).
Administration. In contrast to a usual SFB which is centered around a single person, there was a frequent change of the Speaker. The first Speaker was Deuber, succeeded by Fischer in 1992. Actually, this was a kind of rebellion: Deuber was blamed of misusing his position as a Speaker, of hiding information which he obtained from the DFB. In 1994, Götze was elected. I was Speaker 1996-1998, then Deuber was elected again. At that time, he was aware of his illness, but agreed to serve again, at least for a short period. Finally, after his death in 1999, Götze was Speaker for a second time.
But I should mention not only the Speakers, but also the secretaries, since they did a lot of the work (and all the visitors will remember them well). It was Ms Mehler, and later, in addition, Ms Westerholz, Ms Cole and Ms Zaepernick, who were running all the business. When Ms Mehler was hired by the faculty Deuber was unhappy, since she was recommended by a secretary who refused to prepare coffee for the dean. He himself never minded preparing coffee, even for a secretary. Ms Mehler prepared coffee, prepared meetings, took care of all the guests (sometimes they have strange wishes).
And I should mention Carstens, a professor inside the realm of Deuber. He never applied for a project on his own, but he assembled all the applications and all the reports. He did know how to please both the research council and the state North Rhine-Westphalia (after all, he was also a local politician - in some sense, one might say, that he was (like in Chinese universities) the representative of the Party).
5. The title, the theme.
The press release concerning the establishment of the SFB stated: The topic ranges from algebraic topology to discrete stochastic models. The aim is to pick up questions from physics, chemistry, biology, economics and informatics towards possible applications. The references to physics, chemistry and biology show the hand-writing of Dress. As far as I know, no-one else from the SFB cared about such applications. The reference to information theory is of course visible in Ahlswede's project B2.
The title of the SFB uses the word discrete. At that time, Discrete Mathematics was not yet a topic of public concern. Apparently, when the Senate of the DFG heard the title, there were hesitations: the title seemed to sound like secret activities, like clandestine undercover mathematics, may-be like war research? Note that in English there is the difference between discrete and discreet (with double e), in German, there is just the single word diskret.
Deuber himself often used as title the wording Discrete Mathematics in contrast to the official title which sounds similar, but is quite different: Discrete Structures in Mathematics, you could say: discrete structures in a non-discrete world, for example the use of algebraic structures to describe topological spaces. Deuber liked to compare discrete and non-discrete mathematics with digital and mechanical watches. But I remember that Fischer immediately drew the attention to the Unruh, the balance wheel: this is the time-keeping device in a mechanical watch which transforms a rotating motion into discrete impulses ...
When Waldhausen gave a promotional lecture at the beginning of the SFB, he started, as everyone expected, with discrete invariants for topological spaces, say discrete rings - but immediately shifted the attention to his brave new rings (the ring spectra). The so-called brave new algebra is really a decisive step away from the usual discrete algebra to a non-discrete setting.
So there were many different, even conflicting interpretations about the theme of the SFB.
What are discrete structures in mathematics? Let me mention an example which became popular quite recently, the sets of non-crossing partitions. The number of (classical) non-crosssing partitions of n is just the n-th Catalan number Cn. Note that the binomial coefficient binom{2n}n is divisible by n+1, and Cn = 1/(n+1) binom{2n}n is the corresponding quotient. The sequence of Catalan numbers is 1, 1, 2, 5, 14, 42, 132, .... (as you see, C5 is the famous number 42). They are popular in recreational mathematics, but arise in many different parts of mathematics. Often, this means that non-crossing partitions can be invoked. The non-crossing partitions have very pleasant properties: for example, they form a lattice with self-duality.
Non-crossing partitions play a prominent role as index sets for the free convolution (in free probability theory), as well as for exceptional subcategories (in the representation theory of a linear quiver). In this way, the non-crossing partitions now provide a missing link in our cooperation graph, namely between project B3 (Götze) and my project C2.
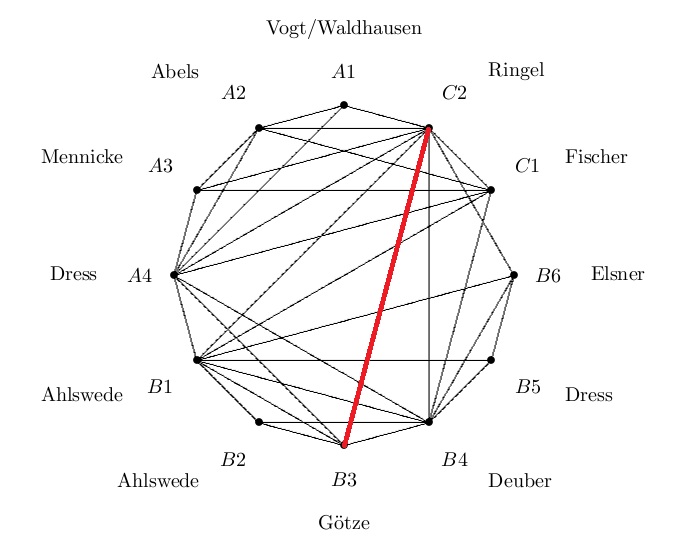
This link could not have been foreseen in 1989. The use of non-crossing partitions in probability theory was started in 1994 by Speicher, in representation theory of algebras even much later. We see that interesting connections may pop up quite suddenly, and may be completely unexpected. This connection turned out to be an important theme in the new SFB 701, but already during the time of the old SFB, Götze pushed the topic, insisting that non-crossing partitions should be relevant in representation theory (how could he know? - but he was right!)
As I mentioned, many topics considered in the SFB were related to group theory, and so it would have been also with non-crossing partitions and their generalizations. Here we consider certain subsets of a Coxeter group G: the given generators endow G with a poset structure and the (generalized) non-crossing partitions are those which are smaller or equal to a fixed Coxeter element.
Of course, there are many other decisive discrete structures in mathematics. Of special importance are groups, posets, simplicial sets, and these were the main keywords mentioned in the SFB application. Also, there are the root systems An, Bn, ... known from Lie theory. In my opinion, they are the basic invariants of what is going on in the world. Again, these are decisive discrete structures. The traditional Catalan combinatorics is just the An-case of a general combinatorial scheme which exists for all Dynkin types.
6. The activities of the SFB.
Publications. This was the time when electronic data transfer was just at its beginning. When I became Speaker of the SFB, I started the SFB home-page in 1996, but the system administrator of the faculty immediately shut it down, since he did not like some formulations. Thus, the dean of the faculty had to intervene.
There was the preprint series of the SFB: with blue covers, over 1000 volumes have appeared. It included preprints of publications, but also other materials, say lecture notes and computational data.
Seminars, conferences, festivities. I should report about joint seminars, an internal colloquium, a study group on the Hilbert problems, also about many kinds of social gatherings and festivities ... . There were some exciting conferences. For example: Fischer's 60th Birthday. Conway accepted to come, he gave several lectures, also one for a general audience, devoted to polyhedra. When Convey suggested the creation of a polyhedra park, Dress offered to built such a park virtually. But Conway replied that for a virtual park he would pay only virtual money. And there was Ahlswede's 60th Birthday: with proceedings in 3 volumes, but with a lot of troubles since he promised that the SFB can be charged for the printing costs ... . Finally, Ahlswede had to pay everything by himself.
The Guest program. As I mentioned, to focus on a guest program was quite special for an SFB. There were many mathematicians from the former Soviet Union and there was the saying that in the tea room of the Bielefeld SFB, the usual language spoken was Russian ... Also there were always several visitors from China. Jacques Tits coming from Bonn to to Bielefeld as a referee, was happy to be able to practise here his Chinese.
Looking at the long and impressive list of guests, it is impossible for me to select a short condensed list of names (but if you have time ...). Thus let me just copy from the final report the names which were highlighted there (even if the selection is not really balanced: there is an obvious dominance of part B, see the first two rows):
 N.Cai |
 L.Khachatrian |
 V.Bentkus |
 S.Bobkov |
||||
 V.I.Bogachev |
 Z.M.Ma |
 L.Friedland |
|||||
 T.Pirashvili |
 E.Vinberg |
 G.Margulis |
 I.Reiten |
||||
(all the pictures but Bobkov's are from the SFB-picture collection, these are polaroid photos made in the offices. For Bobkov, I could not find such a picture.)
The selection was not intended to mention famous names, but to stress long-standing cooperations. Margulis got a Fields medal, but also other Fields medalists were quite frequently visiting Bielefeld. For example Zelmanov. Margulis and Reiten were here as Humboldt prize recipients, as were many others....
Let me also draw attention to some collaborations, just seen from my own project C2. Friedland was invited by Elsner (part B), Pirashvili by Waldhausen (project A1), Vinberg and Margulis by Abels and Helling (A2, A3). I was very happy about all these invitations. There were many contacts with Friedland, based on his interest in all kinds of matrix problems, many of which can be reformulated in terms of quivers. And Pirashvili: the research interests mentioned on his home page (homological and homotopical algebra, polynomial functors, Leibniz algebras, triangulated categories) fit well into the range of themes which have always been discussed in C2.
Have a look: 7 out of the 11 mathematicians are Russian speaking, of course not all are Russians, but from Lithuania, from Georgia, from all parts of the former Soviet-Union, from countries with a strong mathematical tradition. There are two Chinese mathematicians. There is one American, and Idun Reiten from Norway.
If you are surprised that there is just one woman mentioned (Idun Reiten, a very prominent and frequent collaborator with project C2), I should tell you the following story: during the SFB-period, namely in 1998, there was the ICM in Berlin. Idun Reiten was invited as a speaker and I was asked by the Berlin organizing committee to introduce her - no: to introduce him: Herrn Idun Reiten. Berlin could not imagine that an important mathematician with a slightly uncommon first name could be female.
7. The Graduate College Mathematics (1990-1993).
At the time the SFB was established, the research council announced a new (but controversial) program: to create special graduate schools. Bielefeld applied, and the application was immediately successful. After all, when the SFB was inaugurated, the referees had stressed their hope that Bielefeld would take care of young academics, thus it seemed self-evident for the DFG to grant a graduate college to Bielefeld. Applications by other universities, for example Bonn and Münster, were delayed, since these universities had problems mainly with arranging sufficient office space. In this way, the Bielefeld graduate college was the first in Germany for mathematics.
The result was a big outcry by a lot of mathematicians: How could Bielefeld dare to have a graduate school before say Bonn and Münster had one. Also the title: just "Mathematics", was considered as too presumptuous. Bielefeld dared to feel responsible for all of mathematics, and not just the little corner say of discrete structures?? Hirzebruch was upset, Brieskorn was upset... I remember long and frustrating discussions. Thus, after 3 years, Bielefeld lost its graduate school: Only few reasons were formulated; a decisive argument was that there were self-organized seminars by students, which the referees did not like.
As I mentioned, when the SFB was founded, the referees had expressed their hope that Bielefeld would take care of young academics. But this was meant not as praise but as a slap in the face ...
When the graduate college ended, I blamed its chairman for this disaster. I should have realized that it was not at all his fault: that the sudden end was not so sudden, but predetermined from its start. Thus, I really have to apologize to him.
8. The Dead.
Looking back at the participating scientists which were named in the first application, one should draw attention to those who already have passed away:
 Rudolf Ahlswede 1936-2010 |
 Hans-Georg Carstens 1945-2012 |
 Dieter Happel 1953-2012 |
 Rainer Vogt 1942-2015 |
 Detlef Voigt 1938-2012 |
In various ways, all of them have contributed very essentially to the success of the SFB.
Some mathematicians prefer to work at home, some prefer to work in the office and it is of course a privilege that one has this choice. But you may notice that all those from Bielefeld who now are dead, used to work in the office. They were working all the day in a building now known to have been full of PCB, a building full of poison (but some were also heavy smokers).
9. The footing.
Let me end my report with an outline of the footing of the SFB in the research environment of the state of North Rhine-Westphalia, but also inside Bielefeld University.
The state NRW. At that time the state was not really interested in research (what about today?). There is a famous quotation of the then responsible minister Gabriele Behler (she started to be minister for education in 1995, and from 1998 to 2002, she was responsible also for science and research)
 |
"We do not need expensive top universities" Gabriele Behler |
| (NW, 03.09.1998, p.18) |
Fortunately, top research in mathematics is not really expensive, thus we survived.
The rector. When the SFB was founded, Grotemeyer, a mathematician, was rector already for 20 years (Remmert used to call him His Permanence) - he strongly supported all our applications, but he had to retire in 1992.
In contrast, his successor (a professor for pedagogical psychology) had a strong bias against mathematics (for example, at that time, Bielefeld's pedagogy got famous (or infamous) for advocating a severe cutback of mathematics in high school: The newspapers shortened this initiative to the slogan Seven years of mathematics are sufficient). For the assessment session in 1994, the rector did not even deliver the usual welcome address (after all, it is the rector who officially signs the application for an SFB). The referees were upset, but they realized the difficult footing of mathematics inside this university.
The senate. The hiring policy of Mathematics was a big challenge for the university: The mathematicians insisted on standard rules: strict prohibition of internal appointments of professors, complete information about all applicants given to the referees, the quest for further possible candidates ..., these rules were horrifying for many other faculties. They were afraid that such a procedure could become a requirement for the whole university.
As I mentioned, Bielefeld was created as a research university, but already the second rector tried to reduce it to a regional institution. Mathematics in Bielefeld always insisted on a strive for excellence. Bielefeld University is rightly proud that in the new 2020 Times Higher Education ranking, Bielefeld has the rank 166, in contrast to rank 250 in the previous 2019 ranking. However, one should notice that in the years 2011 - 2015, the rank of Bielefeld University had severely dropped year by year. There is the parallel QS ranking of the top universities, where Bielefeld University dropped in the last years from the range 301-350 in the 2012 ranking to the range 751-800 in the 2020 ranking (Bielefeld mathematics remained quite stable in the range 201-250).
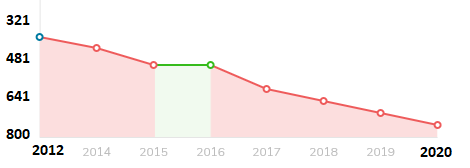 |
| Bielefeld University in the "QS World Universities Ranking" |
Of course, all these rankings are quite questionable, but still they indicate some tendencies.
I have to apologize that I have presented just some data and some personal recollections and remarks. I am aware that a report on a research institute should rather focus attention on the research advances. But that is quite difficult to achieve in short time, for a general audience. Fortunately, I can refer to the internet. There, parts of the final SFB-report are exhibited, and there you can find sufficient hints on the mathematical achievements.
The EMS Newsletter published in 2013 an article on Unity and Disunity in Mathematics (witty, but quite shallow). The authors write: We believe that the phrase unity of mathematics expresses a dream, an ideal that doesn't exist. Of course, it is a dream, an ideal. But it seems worthwhile to work towards this ideal. This was one of the main aims of the SFB.
Quelle: Claus Michael Ringel, The SFB 343 (1989 - 2000)