Collection of PhD theses of (former)
members of the research group
PhD thesis
jr210 Jens Rottmann-Matthes.
Computation and stability of patterns in
hyperbolic-parabolic systems
This work is devoted to the stability analysis and numerical long
time-simulation of relative equilibria in partial differential
equations. The simplest examples of nontrivial relative equilibria − or patterns −
are traveling waves. These arise in a wide range of applications like
nerve axon equations or reaction-diffusion models.
Due to their relevance, the stability of traveling waves has been
considered by many authors. Important contributions are
made by [Evans, 1972--1975], [Sattinger, 1976], [Henry, 1981], and
[Bates and Jones, 1989], to name just a few.
A major difficulty with the numerical long-time simulation of relative
equilibria arises from the fact that the relevant part of the solution
typically leaves the computational domain. Here the freezing method is a
possibility to counter this problem. It is presented in a very general
setting and justified for a large class of equations.
Originally the method was introduced
independently by [Beyn and Thümmler, 2004] and [Rowley et al., 2003].
Its basic idea is to split the evolution into a symmetry
and a shape part. In practice, the method leads to a partial
differential algebraic equation (PDAE).
We consider traveling waves in hyperbolic Cauchy
problems of the form
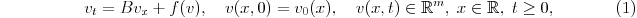
and also in coupled hyperbolic-parabolic problems
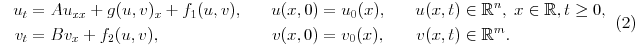
Such systems are also considered in [Kreiss et al., 1994].
We present stability theorems for these equations which show the
exponential stability of traveling waves (fronts and pulses).
Moreover, the rate of
convergence is obtained from the spectrum of the linearization.
Our method of proof is a new combination of a nonlinear change of
coordinates as in [Henry, 1981] and the Laplace transform technique as in
[Kreiss et al., 1994]. The coordinate change leads to a
hyperbolic(-parabolic)
PDAE system that is
closely related to the freezing method. For this system existence
results and resolvent estimates are shown so that the Laplace transform
can rigorously be applied and yields stability. In particular,
our proof clarifies the treatment of
the asymptotic phase.
Furthermore, we prove that the freezing method can be applied to
(1) and (2) and show that it converges exponentially
and provides asymptotically with time the correct speed and profile of
the traveling wave. This is important from a numerical point of view and
extends results by [Thümmler, 2005]
to another class of equations.
In the final chapter, the theory is applied to several important
examples (like the FitzHugh-Nagumo system) and the freezing method is
tested for these.
The freezing method is also tested for systems which are not covered by
the theory. A particular interesting example
is the viscous Burgers' equation for which the freezing method enables
us to observe metastability numerically.
-
| Publisher: | Shaker Verlag, Aachen (2010) |
| Pages: | 196 |
| ISBN-10: | 3-8322-9064-8 |
| ISBN-13: | 978-3-8322-9064-1 |