|
|
Talks
Workshops
Seminars
-
Raphael Kruse (TU Berlin)
: On randomized time-stepping methods for non-autonomous evolution equations
with time-irregular coefficients
2019/02/18, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk, we consider the numerical approximation of Carathéodory-type
ODEs and of nonlinear and non-autonomous evolution equations
whose coefficients may be irregular or discontinuous with respect to the time
variable. In this non-smooth situation, it is difficult to construct numerical
algorithms with a positive convergence rate. In fact, it can be shown that any
deterministic algorithm depending only on point evaluations may fail to
converge.
Instead, we propose to apply randomized Runge-Kutta methods to such
time-irregular evolution equations as, for instance, a randomized version of the
backward Euler method. We obtain positive convergence rates with respect to the
mean-square norm under considerably relaxed temporal regularity conditions. An
important ingredient in the error analysis
consists of a well-known variance reduction technique for Monte Carlo methods,
the stratified sampling.
We demonstrate the practicability of the new algorithm in the case of a fully
discrete approximation of a parabolic PDE.
This talk is based on joint work with Monika Eisenmann (TU Berlin),
Mihály Kovács and Stig Larsson (both Chalmers University
of Technology) as well as Yue Wu (U Edinburgh).
-
Christian Pötzsche (Alpen-Adria Universität Klagenfurt)
: Numerical Dynamics of Integrodifference Equations
2018/07/17, 16:15, U2-147, Seminar Numerical Analysis
Abstract: Integrodifference equations (IDEs for short) are a popular tool in
theoretical ecology to describe the spatial dispersal of populations
with nonoverlapping generations. From a mathematical perspective,
IDEs are recursions on ambient spaces of continuous or integrable
functions and thus generate infinite-dimensional dynamical systems.
Hence, for simulation purposes an appropriate numerical approximation
yielding a finite-dimensional state space is due. Our goal is to study
dynamical properties of IDEs (e.g. existence of reference solutions,
attractors, invariant manifolds) which are preserved under corresponding
numerical methods and to establish convergence for increasingly more
accurate schemes.
-
Ingo Könemann
: Stability of Nonautonomous Differnce Equations
2018/07/06, 14:15, V5-148, AG Dynamische Systeme
Abstract:
-
Janosch Rieger (Monash University, Melbourne)
: A Galerkin-type approach to shape
optimisation in the space of convex sets
2018/06/25, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk, I will discuss spaces of polytopes with fixed outer
normals and their use in theoretical and practical
shape optimization. These spaces possess a natural
system of coordinates, and all admissible
coordinates can be characterized by a linear
inequality, which is handy both from an analytical as well as
from a computational perspective.
These polytope spaces approximate the space of all nonempty convex and
compact subsets in Hausdorff distance uniformly on
every bounded set, so they behave like classical
Galerkin approximations to function spaces.
I will show that for simple shape optimization
problems, the set of global minimizers of auxiliary problems
posed in the polytope spaces converges to the set of global minimizers
of the original problem.
-
Evelyn Buckwar (JKU Linz)
: A stability vs. Monte-Carlo integration problem for SDEs
2017/12/18, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we investigate the interplay of almost sure and mean-square
stability for linear SDEs and the Monte Carlo method for estimating the
second moment of the solution process. In the situation where the zero
solution of the SDE is asymptotically stable in the almost sure sense but
asymptotically mean-square unstable, the latter property is determined by
rarely occurring trajectories that are sufficiently far away from the
origin. The standard Monte Carlo approach for estimating higher moments
essentially computes a finite number of trajectories and is bound to miss
those rare events. It thus fails to reproduce the correct mean-square
dynamics (under reasonable cost). A straightforward application of variance
reduction techniques will typically not resolve the situation unless these
methods force the rare, exploding trajectories to happen more frequently.
Here we propose an appropriately tuned importance sampling technique based
on Girsanov's theorem to deal with the rare event simulation. In addition
further variance reduction techniques, such as multilevel Monte Carlo, can
be applied to control the variance of the modified Monte Carlo estimators.
As an illustrative example we discuss the numerical treatment of the
stochastic heat equation with multiplicative noise and present simulation
results.
This is joint work with Markus Ableidinger and Andreas Thalhammer.
-
Erika Hausenblas (Montanuniversität Leoben)
: The Stochastic Gray Scott system
2017/11/06, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Reaction and diffusion of chemical species can produce a variety of
patterns, reminiscent of those often seen in nature. The Gray Scott system
is a coupled equation of reaction diffusion type, modelling these kind of
patterns. Depending on the parameter, stripes, waves, cloud streets, or
sand ripples may appear.
These systems are the macroscopic model of microscopic dynamics.
Here, in the derivation of the equation the random fluctuation of the
molecules are neglected.
Adding a stochastic noise, the inherit randomness
of the microscopic behaviour is modelled. In particular, we add a time
homogenous spatial Gaussian random field with given spectral measure.
In the talk we present our main result about the stochastic Gray Scott
system.
In addition, we introduce and explain an algorithm for its numerical
approximation by a Operator splitting method. Finally we present some
examples illustrating the dynamical behaviour of the stochastic Gray
Scott system.
-
Anna Khripunova-Balci (Vladimir State University)
: On p(x)-connectedness of periodical measures
2017/10/30, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We obtain the Gamma-convergence result for the sequence of
integral functionals with non-standard growth conditions and measures. The
key proberties that allows to pass to the limit in such problems is the so
called p(x)-connectedness of measure. We also consider some connected
problems or Sobolev-Orlich spaces with respect to measures.
-
Sebastian Schwarzacher (Bonn): Existence and discretisation of strong solutions to rate
independent systems
2017/10/23, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Rate-independent systems arise in a number of applications.
Usually, weak solutions to such problems with potentially very low
regularity are considered, requiring mathematical techniques capable of
handling nonsmooth functions. The subject of this talk introduces a
strategy which in contrast to existing approaches directly implies
existence of Hölder-regular strong solutions for a class of
rate-independent systems. Additionally higher regularity results are
presented that guarantee the uniqueness of strong solutions. The proof
proceeds via a time-discrete Rothe approximation and careful elliptic
regularity estimates. Finally, a space-time discretization will be
introduced of which we prove the convergence with a rate to the (strong)
solution.
The content of the talk is a joint work with F. Rindler (Warwick
University) and E. Süli (Oxford University).
-
Janosch Rieger (Monash University Melbourne)
: Applications of the solvability theorem for
relaxed one-sided Lipschitz inclusions
2017/07/17, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The solvability theorem guarantees the
existence of a solution of
a relaxed one-sided Lipschitz algebraic inclusion
within a certain ball.
This localisation can be used to characterise the
boundary of the reachable
set of a control system and, as a consequence, omit
many redundant
operations for its numerical approximation. It also
induces a numerical
scheme for the solution of the algebraic inclusion,
provided the right-hand
side is Lipschitz as well.
-
Tomasz Cieslak (Instytut Matematyczny Polskiej Akademii
Nauk, Warschau)
: Kaden's spiral and velocity of vortex sheet represented
by the moments of its vorticity.
2017/07/03, 16:15, V5-148, Seminar Numerical Analysis
Abstract: I will review our recent common results with
M.Szumanska, K. Oleszkiewicz and M. Preisner concerning
the self-similar vortex sheets and their role in the 2d inviscid and
incompressible flow.
In particular I will show how to compute the velocity of Kaden's spiral
and show that the energy is dissipated by such an object.
-
André Wilke (Bielefeld)
: Analysis and numerics of total variation flow
2017/06/30, 14:15, V5-148, AG Dynamische Systeme
Abstract:
-
Franz Gmeineder (Oxford)
: On the Neumann problem for variational integrals in BV
2017/06/19, 15:00!, V2-105/115, Seminar Numerical Analysis
Abstract: In this talk I give an overview of old and new results regarding
the solvability of variational problems of linear growth, actually to be
dealt with in the space BV of functions of bounded variation, in Sobolev
spaces. Contrasting the rather restrictive results available in the
Dirichlet case, we shall focus on the variational formulation of the Neumann
problem on BV which allows for Sobolev solutions even in presence of high
degeneracy of the integrands' ellipticity.
This is joint work with L. Beck
(Augsburg) and M. Bulicek (Prague).
-
Stefanie Hittmeyer (Auckland)
: The geometry of blenders in a three-dimensional
Hénon-like family
2017/06/19, 16:15, , Seminar Numerical Analysis
Abstract: Blenders are a geometric tool to construct complicated dynamics in
diffeomorphisms of dimension at least three and vector fields of dimension
at least four. They admit invariant manifolds that behave like geometric
objects which have dimensions higher than expected from the manifolds
themselves. We consider an explicit family of three-dimensional Hénon-like
maps that exhibit blenders in a specific regime in parameter space. Using
advanced numerical techniques we compute stable and unstable manifolds in
this system, enabling us to show one of the first numerical pictures of the
geometry of blenders. We furthermore present numerical evidence suggesting
that the regime of existence of the blenders extends to a larger region in
parameter space.
This talk is based on joint work with Bernd Krauskopf,
Hinke Osinga and Katsutoshi Shinohara.
-
Erwan Faou (Rennes)
: On the long time stabiity of travelling wave for
the discrete nonlinear Schrödinger equations
2017/06/09, 14:15, , Seminar Numerical Analysis
Abstract: I will discuss the possible existence of travelling wave solutions
for discrete nonlinear Schrödinger equations on a grid. I will show the
influence of the nonlinearity in this problem and give some partial results
for the long time stability. This is a joint work with Dario Bambusi,
Joackim Bernier, Benoît Grébert and Alberto Maspero.
-
Dominic Breit (University of Edinburgh)
: Stationaly Solutions to the compressible
Navier-Stokes system driven by stochastic Forces
2017/05/22, 16:15, , Seminar Numerical Analysis
Abstract: We study the long-time behavior of solutions to a
stochastically driven Navier-Stokes system describing the motion of
a compressible viscous fluid driven by a temporal multiplicative white
noise perturbation.
The existence of stationary solutions is established in the framework
of Lebesgue-Sobolev spaces pertinent to the class of weak martingale
solutions. The methods are based on new global-in-time estimates and a
combination of deterministic and stochastic compactness arguments.
In contrast with the deterministic case, where related results
were obtained only under rather restrictive constitutive assumptions for
the pressure, the stochastic case is tractable in the full
range of constitutive relations allowed by the available existence theory.
This can be seen as a kind of the noise on the global-in-time solutions.
-
Noel Walkington (Carnegie Mellon University, Pittsburgh)
: Numerical Approximation of Multiphase Flows in
Porous Media
2017/05/19, 14:15, V5-148, AG Dynamische Systeme
Abstract: This talk will review structural properties of the equations
used to model geophysical flows which involve multiple components undergoing
phase transitions. Simulations of these problems only model the gross
properties of these flows since a precise description of the physical
system is neither available nor computationally tractable. In this
context mathematics provides an essential foundation to facilitate the
integration of phenomenology and physical intuition to develop robust
numerical schemes that inherit essential.
-
Sebastian Schwarzacher (Prag)
: On compressible fluids interacting with a
linear-elastic shell
2017/05/15, 16:15, , Seminar Numerical Analysis
Abstract: We study the Navier--Stokes equations governing the motion
of an isentropic compressible fluid in three dimensions interacting
with a flexible shell.
The latter one constitutes a moving part of the boundary of the physical
domain. Its deformation is modeled by a linearized version of Koiter's
elastic energy.
We discuss the existence of weak solutions to the corresponding system of
PDEs provided the adiabatic exponent satisfies \(\gamma>\frac{12}{7}\)
\(\gamma>1\) in two dimensions). The solution exists until the moving
boundary approaches a self-intersection.
This provides a compressible counterpart of the results in
[D. Lengeler, M. Ruzicka, Weak Solutions for
an Incompressible Newtonian Fluid Interacting with a Koiter Type Shell.
Arch. Ration. Mech. Anal. 211 (2014), no. 1, 205--255] on incompressible
Navier--Stokes equations.
It is a joint work with D. Breit (Heriot-Watt Univ. Edinburgh).
-
Tsiry Randrianasolo (Montanuniversität Leoben)
: Time-Discretization scheme of stochastic 2-D
Navier-Stokes Equations by a Penalty-Projection method
2017/05/08, 16:15, , Seminar Numerical Analysis
Abstract: A time-discretization of the stochastic incompressible Navier-Stokes problem by penalty
method is analyzed. Our work concerns the nonlinear term which in the stochastic framework prevents
from using a Gronwall argument. Moreover, the approximate solution is slightly compressible and
therefore, the nonlinear does not satisfy the additional orthogonal property which usually in two-
dimension and with a periodic boundary condition allows to get some useful estimates. To tackle these
issues we use the classical decomposition of the solution into an Ornstein-Uhlenbeck process and a
solution of a deterministic Navier-Stokes equation depending on a
stochastic process. The first part is stochastic but linear while the
second one is nonlinear but deterministic. Both sub problems are still
approximated with a numerical scheme based on penalty method. Error estimates for both of them
are derived, combined, and eventually arrive at a convergence in probability with order 1/4 of the
main algorithm towards the initial problem for the pair of variables
velocity and pressure. The strong convergence of the scheme is achieved by means of the Bayes formula.
-
Christian Döding (Bielefeld)
: Traveling Oscillating Fronts in Parabolic Evolution
Equations"
2017/02/03, 14:15, , AG Dynamische Systeme
Abstract: We consider complex-valued parabolic evolution equations in one space
dimension that are equivariant under spatial translation and, in
addition, admit a symmetry under complex phase-shift. A major example is
the complex quintic Ginzburg-Landau equation. In this talk we are
interested in traveling oscillating front solutions. The solutions admit
a fixed profile, which travels in space and oscillates in the time
evolution, by multiplication with a time-dependent rotational term.
Besides, the profile converge to the zero steady state on the one side
and to a complex-valued but nonzero steady state on the other. The
stability behavior, especially the nonlinear stability, of the solutions
is almost unknown. I will give an introduction into the topic and will
show how to compute such solutions numerically as heteroclinic orbits of
a three dimensional dynamical system. Further, I will derive the
equivalent real-valued system, state the corresponding Cauchy-problem
and give a first spectral analysis of the occurring operator, which is
relevant for studying the nonlinear stability of these solutions.
-
H.J. Schroll (University of Southern Denmark, Odense)
: Computational Modeling of Fluorescence Loss in
Photobleaching
2017/01/16, 14:15, V5-148, Seminar Numerical Analysis
Abstract: A quantitative analysis of intracellular transport
processes is essential for the diagnosis and improved treatment of
diseases like Alzheimer, Parkinson, lysosomal storage disorders and
arteriosclerosis.
Fluorescence loss in photobleaching (FLIP) is a modern microscopy method
for visualization of transport processes in living cells.
Although FLIP is widespread, only few studies attempt yo derive
quantitative models of the transport processes underlying observed FLIP
image sequences.
This paper presents the simulation of FLIP sequences based on a calibrated
reaction--diffusion system defined on segmented cell images.
The PDE model is conveniently implemented in the automated Finite Element
software package FEniCS.
By the use of a discontinuous Galerkin method, the computational
complexity is drastically reduced compared to continuous Galerkin methods.
Using this approach on green fluorescent protein (GFP), we are able to
determine its intracellular diffusion constant, strength of localized
hindrance to diffusion as well as the permeability of the nuclear membrane
for GFP passage, directly from the FLIP image series.
This sets the stage towards detailed description of the transport dynamics
underlying observed FLIP data in other applications.
-
Jens Rottmann-Matthes (Karlsruhe)
: An IMEX-RK scheme for capturing similarity
solutions in multi-dimensional Burger's equation
2016/12/12, 14:15, X-E0-002 !!, Seminar Numerical Analysis
Abstract:
The topic of the talk are similarity solutions occuring in
multi-dimensional Burger's equation. In the first part we present a simple derivation of the
symmetries that appear in a family of general Burgers' equation in \(d\)-space dimensions.
We use these symmetries to derive an equivalent partial differential
algebraic equation (freezing system).
In the second part we concentrate on the numerical approximation of this
PDAE. We introduce a new and easily implementable numerical scheme, based on
an IMEX-Runge-Kutta approach for a method of lines (semi-)discretization of
the freezing PDAE. We prove second order convergence for the time
discretization at smooth solutions.
Numerical experiments show that our method enables us to do long time
simulations and obtain good approximations of similarity solutions to the
multi-dimensional Burgers' equation by direct forward simulation. The method
also allows us without further effort to observe meta-stable behavior near
N-wave-like patterns.
Moreover, the experiments give numerical evidence that the method is indeed
second order convergent for all positive values of viscosity. Because the
multi-dimensional Burgers' equation can be considered as a PDE with a
parabolic or hyperbolic dominating part for large, resp. very small
viscosities, our findings suggest that the scheme is indeed suitable
for the discretization of the freezing PDAE for general coupled
hyperbolic-parabolic PDEs.
-
Christian Meyer (TU Dortmund)
: Optimal Control of Variational Inequalities
2016/11/21, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Many applications are modeled by variational inequalities (VIs), in
particular in computational mechanics. Classical examples are elastoplastic
deformations, contact problems, or damage evolution. The solution mappings
associated with these models are in general not Gâteaux-differentiable.
Therefore, standard techniques in optimal control based on the
control-to-state mapping are not applicable. Remedies are regularization and
relaxation approaches as well as techniques that employ the limited
differentiability properties of the solution map associated with the
respective VI. We will present several of these approaches from a theoretic
as well as numerical perspective.
-
D. Otten (Universität Bielefeld)
: Fredholm Properties and \(L^P\)-Spectra of
Localized Rotating Waves in Parabolic Systems
2016/11/18, 14:15, V5-148,
Abstract:
Rotating waves are special solutions of reaction-diffusion systems which rotate at
constant velocity while maintaining their shape. Nonlinear stability results for such waves are
usually based on spatial behavior of the wave profile and on spectral properties of the linearization.
The linearization, obtained by linearizing the co-rotating frame at the wave profile, turns
out to be an additive variable coefficient perturbation of a complex-valued Ornstein-Uhlenbeck
operator.
In this talk we first present a short review about previous results on exponential decay of rotating
waves. We then investigate Fredholm properties of the linearization, derive the Fredholm
alternative and show under suitable assumptions that eigenfunctions and their adjoints decay
exponentially in space. We then provide different techniques to derive certain subsets of the
spectrum of the linearization. The main idea is to reduce the eigenvalue problem of the linearized
operator to a finite-dimensional one. For this purpose, we first derive the dispersion set,
which is affected by the far-field behavior of the wave, and show that it belongs to the essential
\(L^P\)-spectrum. We then derive the symmetry set, which is induced by the underlying group
symmetries, and show that it belongs to the point \(L^P\)-spectrum. From Fredholm properties we
deduce exponential decay of the associated eigenfunctions and their adjoints. Finally, we present
numerical results for spinning solitons that appear in the cubic-quintic complex Ginzburg-Landau
equation.
-
Dimitra Antonopoulou (University of Chester)
: Existence and Regularity of Solution for a
stochastic Cahn-Hilliard/Allen-Cahn Equation with unbounded Noise Diffusion
2016/11/07, 14:15, V5-148, Seminar Numerical Analysis
Abstract: The Cahn-Hilliard/Allen-Cahn equation with noise is a simplified mean field
model
of stochastic microscopic dynamics associated with adsorption and
desorption-spin flip mechanisms
in the context of surface processes. For such an equation we consider a
multiplicative
space-time white noise with diffusion coefficient of linear growth. Applying
technics from semigroup
theory, we prove local existence and uniqueness in dimensions d = 1, 2, 3.
Moreover, when the diffusion coefficient satisfies a sub--linear growth
condition of order $\alpha$ bounded by 1/3, which is
the inverse of the polynomial order of the nonlinearity used, we prove
for d=1 global existence
of solution. Path regularity of stochastic solution, depending on that of
the initial condition,
is obtained a.s. up to the explosion time. The path regularity is identical
to that proved for
the stochastic Cahn--Hilliard equation in the case of bounded noise
diffusion. Our results are
also valid for the stochastic Cahn--Hilliard equation with unbounded noise
diffusion, for which
previous results were established only in the framework of a bounded
diffusion coefficient. As expected from the theory of parabolic
operators the bi--Laplacian operator seems to be dominant in the combined model.
Joint work with G. Karali and A. Millet.
-
W.--J. Beyn (Universität Bielefeld)
: Stability and Computation of
waves in second order evolution equations
2016/10/24, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we consider traveling waves of a semilinear
damped wave equation. We show how the freezing method generalizes from first to second order evolution equations by transforming the original PDE into a partial differential algebraic equation (PDAE). Solving a Cauchy problem via the PDAE generates a comoving frame in which the solution becomes stationary, and an additional variable which converges to the speed of the wave, provided the original wave has suitable stability properties. A rigorous theory of this effect is presented in one space dimension, building on recent nonlinear stability results for waves in first order hyperbolic systems. Numerical examples demonstrate the applicability of the method, and generalizations to rotating patterns in several space dimensions indicate its scope.
-
Barnabas M. Garay
(Faculty for Information Technology and Bionics, Pazmany Peter Catholic
University, Budapest)
: On metastable rotating waves in Chua-Yang ring networks
2016/08/19, 14:15, V5-148, AG Dynamische Systeme
Abstract: The topic of the this talk is the phenomenon of long-transient
oscillations observed experimentally in a Chua-Yang electrical circuit.
Such periodic oscillations seem to be asymptotically stable for several
seconds --- a time almost as long as eternity in electrical engineering. In a
piecewise linear ODE system with rotational symmetry modelling a circular
cellular neural network array with a saturated, three-segment piecewise
linear activation and two-sided, not-necessarily cooperative
interconnections, exponentially small lower and exponentially small upper
estimates for the critical Instability Gap are presented.
M.Forti, B.M.Garay, M.Koller, L.Pancioni, Long transient oscillations in a
class of cooperative cellular neural networks, Int. J. Circuit Theory
Applications} 43(2015), 635.
M.DiMarco, M.Forti, B.M.Garay, Koller, L.Pancioni, Floquet multipliers of a
metastable rotating wave in a Chua-Yang ring network, J. Math. Anal. Appl.
434(2016), 798-836.
-
Thorsten Hüls: A contour algorithm for computing stable fiber bundles of
nonautonomous, noninvertible maps
2016/06/06, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Stable fiber bundles are the nonautonomous analog of stable
manifolds and these objects provide valuable information on the
underlying dynamics. We propose an algorithm for their approximation
that is based on computing zero contours of a particular operator.
The resulting program applies to a wide class of models,
including noninvertible and nonautonomous discrete time systems.
Precise error estimates are provided and fiber bundles are computed
for several examples.
Finally, we apply the contour algorithm to (non)autonomous ODEs.
For the famous three-dimensional Lorenz system, we calculate
several approximations of the two-dimensional Lorenz manifold.
-
Matthew Salewski (TU Berlin) : Equivariance and reduced-order modelling
2016/05/27, 14:15, V5-148, AG Dynamische Systeme
Abstract: The construction of reduced-order models from a dynamical
system can be enhanced when one uses properties of the system,
such as the equivariance
of the system under the action of a Lie group. This allows the dynamics to
be reduced to a subspace where the action of the group has been removed.
This effect can be advantageous when applied to systems of
transport-dominated phenomena, for example a moving localized pulse or
front which generally pose problems for accurate modeling.
Here, i discuss a protocol for constructing reduced-order models using
equivariance, and demonstrate this protocol with simple systems exhibiting
transport-dominated phenomena. In addition, I will comment on systems
whose equivariance is not explicitly clear and show some approaches used
to deal with this when constructing a model.
-
Arnd Scheel (Minnesota): Defects in Striped Phases
2016/05/09, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Many nonlinear systems admit families of striped solutions,
which are periodic in one spatial variable. A prototypical system is the
Swift--Hohenberg equation with cubic nonlinearity. I will discuss
attempts to describe patterns that deviate from exact spatial periodicity
due to the presence of boundary conditions, inhomogeneities, or
'self--organized' defects.
-
Markus Ableidinger (JUK Linz): Structure preserving splitting integrators for SDEs
2016/03/30, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we will discuss stochastic differential
equations where the solution trajectories are governed by geometric
structures as, e.g. energy
preservation or dissipation. An efficient strategy for constructing
structure preserving integrators is to split the SDE into subsystems which
inherit the geometric structure and build a numerical integrator by
composition of the exact flows of the subsystems. We apply this approach on
SDEs arising in micromagnetism (stochastic Landau-Lifshitz-Gilbert
equation) and neuroscience (stochastic Jansen and Rit Neural Mass Model).
-
Janosch Rieger (Imperial College London): Generalized Convexity and Set Computation
2016/03/18, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
Generalized convexity has mainly been studied in optimization theory with
a focus on generalized convex functions. In this talk, I will give a brief
introduction to convex sets from a support function point of view before
discussing generalized convex sets and their use for set representation
and computation. Some of the content will be work in progress.
-
Stefan Liebscher (Technology Consulting München): The Tumbling Universe: Cosmological Models in
the Big-Bang Limit
2016/01/22, 14:15, V5-148, AG Dynamische Systeme
Abstract: Cosmological models are solutions of the Einstein field
equations. We are interested in the alpha-limit dynamics describing
the early universe.
We will discuss possible model reductions facilitated by symmetry
assumptions. Focus is on Bianchi cosmologies. They yield spatially
homogeneous, anisotropic solutions of the Einstein field equations.
The (backward) attractor of the Bianchi system is composed of the Kasner
circle of equilibria and attached heteroclinic connections. The Kasner
equilibria correspond to self-similar cosmologies. General solutions in
the Big-bang limit follow heteroclinic chains of the attractor and
describe universes which tumble between different self-similar
cosmologies.
-
Hari Shankar Mahato (Universität Erlangen-Nürnberg)
: Homogenization of Some Two-scale Models in Porous Media
2016/01/11, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
A porous medium (concrete, soil, rocks, water reservoir, e.g.) is a
multi-scale
medium where the heterogeneities present in the medium are characterised
by the micro
scale and the global behaviours of the medium are observed by the macro
scale. The
upscaling from the micro scale to the macro scale can be done via
averaging methods.
In this talk, we consider two models: M1 and M2. In M1 diffusion and
reaction of
mobile chemical species are considered in the pore space of a porous
medium. The
reactions amongst the species are modelled via mass action kinetics and
the modelling
leads to a system of multi-species diffusion-reaction equations (coupled
semi-linear partial
differential equations) at the micro scale where the highly nonlinear
reaction rate terms
are present at the right hand sides of the system of PDEs, cf. [2].
In model M2, diffusion, advection and reaction of two different types of
mobile species (type I and type II) are considered at the micro
scale. The type II species are
supplied via dissolution process due to the presence of immobile species
on the surface of the solid parts.
The presence of both mobile and the immobile species
make the model complex and the modelling yields a system of semi-linear partial
differential
equations coupled with ordinary differential equations with jump
discontinuity. For both M1 and M2, the existence of a unique positive
global weak solution is
shown
with the
help of a Lyapunov functional, Schaefer's fixed point theorem and some
regularisation
technique, cf. [2, 3]. Finally with the help of two-scale convergence and
periodic
unfolding, M1 and M2 are upscaled from the micro scale to the macro scale,
e.g. [1, 3].
Some numerical simulations will also be shown in this talk, however for the
purpose
of illustration, we restrict ourselves to some relatively simple 2-
dimensional situations.
References:
[1] G. Allaire, Homogenization and two scale convergence, SIAM Journal of
Mathematical Analysis, 23(6), 1482-1518, 1992.
[2] H.S. Mahato and M. Böhm, Global existence and uniqueness for a system
of nonlinear multi-species diffusion-reaction equations in an H1,p setting,
Journal of Applied Analysis and Computation, 3(4), 357-376, 2013.
[3] H.S. Mahato and M. Böhm, An existence result for a system of coupled
semilinear diffusion-reaction equations with flux boundary conditions,
European Journal of Applied Mathematics, 2014.
-
Péter Koltai (FU Berlin): Coherent Families: Spectral Theory for Transfer
Operators in Continuous Time
2015/12/11, 14:15, V5-148, AG Dynamische Systeme
Abstract:
The decomposition of the state space of a dynamical system into
metastable or almost-invariant sets is important for understanding
macroscopic behavior. This concept is well-understood for autonomous
dynamical systems, and has recently been generalized to non-autonomous
systems via the notion of coherent sets. We elaborate here on the
theory of coherent sets in continuous time for periodically-driven
flows and describe a numerical method to find families of coherent
sets without trajectory integration.
-
David Hilditch (Universität Jena): The formulation, theory and practice of
Numerical Relativity
2015/12/10, 10:15, V4-106, Seminar Numerical Analysis
Abstract:
I will give an introduction to the basic subject matter of Numerical
Relativity. Starting with simple toy problems, I will discuss the
formulation of General Relativity as an initial value problem and the
requirement of well-posedness of the resulting PDE problem. I will
summarize standard numerical methods and outline the major topics of the
field. Finally I will discuss my own work on collapsing gravitational waves
and on the relationship between gauge and coordinate freedom.
-
Jochen Röndigs (Uni Bielefeld): Foundations for General Relativity
2015/12/07, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
With a brief summary of Special Relativity (SR) we introduce the
corresponding mathematical model of flat spacetime, which is called a
Minkowski space, characterised by a special, generalised scalar product
(the Minkowski metric). A short analysis of the spacetime structure, that
is the metric and isometries (Lorentz transformations), is presented
including some of the major consequences of SR. As a preparation for
General Relativity with curved spacetime, which is modeled as a manifold
over a Minkowski space, the basic concepts for differential geometry and
manifolds are introduced. The final goal is to be ready for the Einstein
field equations and the talk about Numerical Relativity on Thursday.
-
Bernhard Lani-Wayda (Uni Gießen): Chaotic motion in delay equations
2015/11/30, 16:15, V5-148, Seminar Numerical Analysis
Abstract: In delay equations, such as \(x'(t) = - \mu x(t) + f(x(t-1))\),
apparently chaotic behavior was frequently observed in numerical
simulations since the 1970s.
Analytical proofs are, generally speaking, still out of reach, but exist
for some examples.
The talk presents some of these examples, the relevant
geometric-topological
structures and the techniques of proof, along with some open problems.
-
Nils Hartmann (Uni Bielefeld): Umkehrpunkte periodischer Lösungen
zeitkontinuierlicher autonomer Systeme
2015/11/27, 14:15, V5-148, AG Dynamische Systeme
Abstract: In diesen Vortrag behandeln wir ausgehend von einer eindeutigen
periodischen Lösung einer autonomen Differentialgleichung bei festem
Parameter die Lösungsfortsetzung im Phasenraum mit variablem Parameter.
Im Anschluss werden wir eine geeignete Testfunktion für quadratische
Umkehrpunkte definieren und je nach verbliebener Zeit deren Regularität
beweisen.
-
Christian Kahle (Uni Hamburg): Control of two phase fluids
using a diffuse-interface model
2015/11/16, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
The simulation of multiphase fluids has attained growing interest in the
last decades. While for one phase flow with the Navier--Stokes system
the basic model is well understood for multiphase system additional
challenges arise by the necessity to track
the transition zones or interfaces between different fluid components.
Methods to track these zones split in two general concepts,
namely representing the interface as a lower dimensional manifold (sharp
interface) and tracking its evolution due to the outer velocity field,
or introducing a phase field function or order parameter for the
description of the distribution of the phases.
A phase field is a smooth indicator function with
distinct values in the two phases that yields a smooth transition between
these values over a small length scale where the interface is located.
In this talk a diffuse interface model is discussed that is consistent
with thermodynamics.
Also a discrete concept that is able to preserve this feature in the
discrete setting is provided.
Based on this stable discrete concept optimal control of two phase fluids
is introduced and analyzed.
-
Thomas Dunst (Uni Tübingen): The Forward-Backward Stochastic Heat Equation:
Numerical Analysis and Simulation
2015/10/26, 16:15, V5-148, Seminar Numerical Analysis
Abstract: I report on recent results to numerically approximate the
forward-backward stochastic heat equation. For this purpose, I start with
showing strong convergence with optimal rates for a spatial
discretization of the backward stochastic heat equation, which is then
extended to strong optimal rates for the forward-backward stochastic heat
equation from optimal stochastic control. A full discretization based on
the implicit Euler method for a temporal discretization, and a least
squares Monte-Carlo method are then proposed and simulation results are
reported.
This talk is based on a joint work with Andreas Prohl (Uni Tübingen).
-
Raphael Kruse (TU Berlin): Numerical approximation of SDEs under a one-sided
Lipschitz condition
2015/10/05, 14:15!!, V2-200, Seminar Numerical Analysis
Abstract: In this talk we present some new results on the numerical
approximation
of stochastic differential equations, which satisfy the so called global
monotonicity condition. In particular, we study the mean-square error of
convergence of the backward Euler method and the BDF2-Maruyama scheme.
The proof relies on new stability results and a priori estimates of the
numerical schemes.
-
Nils Hartmann: Periodische Lösungen zeitkontinuierlicher
autonomer Systeme
2015/07/17, 15:15, V5-148, AG Dynamische Systeme
Abstract: In dem Vortag wird zuerst die Existenz und Eindeutigkeit periodischer
Lösungen in autonomen zeitkontinuierlichen Systemen behandelt.
Danach werden mit Hilfe der Floquet Theorie hinreichende und notwendige
Bedingungen für die orbitale Stabilität periodischer Orbits diskutiert.
Anschließend befassen wir uns mit der Theorie der numerischen Berechnung
von periodischen Lösungen.
-
Seung-Yeal Ha (Seoul): Synthesis of synchronization and flocking:
From Winfree to Cucker-Smale
2015/07/13, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Collective behaviors of complex systems are often observed
in our nature, i.e., flocking of birds, swarming of fishes
and synchronization of pacemaker cells etc. In this talk, we present
recent progress for the unification of flocking and
synchronization in one framework.
For this, we will discuss several mathematical models and how these
models can be studied in the same methodology.
-
Christian Vieth: Konfidenzellipsoide in stochastischen
Differentialgleichungen und die Lyapunov Gleichung
2015/07/10, 15:15, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten die Lyapunov Gleichung
\[ AY+YA^T=-BB^T,\]
die bei bei der Berechnung von Konfidenzellipsoiden stochastisch
metastabiler Gleichgewichte auftritt.
Ziel ist es, Lösbarkeit und Lösungsdarstellungen sowie
numerische Verfahren vorzustellen.
-
Tatjana Stykel (Universität Augsburg): Model reduction of linear and nonlinear
magneto-quasistatic problems
2015/07/03, 14:15, V5-148, Seminar Numerical Analysis
-
Christina Göpfert: An Overview of Topological Entropy and Metric Entropy
2015/06/19, 14:15, V5-148, AG Dynamische Systeme
Abstract: Topological entropy is an invariant under topological
conjugacy. The corresponding notion in ergodic theory is the metric
entropy, which is invariant under conjugacy in the ergodic sense. The
two are connected by the variation principle. An application of these
concepts is an algorithm for computing rigorous upper bounds for
topological entropy by Froyland, Junge and Ochs.
During the talk, we will discuss the aforementioned concepts and
explore how they relate.
-
Amy Novick-Cohen (Technion, Haifa) : Geometric interfacial motions: coupling surface
diffusion and mean curvature motion
2015/06/15, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Mean curvature motion as well as surface diffusion constitute geometric
interfacial motions which have received considerable attention. However in
many applications a complex combination of coupled surfaces appear whose
evolution may be described by coupling these two types of motion. In my
lecture, a variety of physical problems will be described which may be
reasonably
modeled by such motions. While some these problems appear to
require an anisotropic formulation, often an isotropic formulation is helpful
to consider. A panoply of analytic and numerical results will be presented,
in addition to some supporting experimental evidence.
-
Christian Döding (Universität Bielefeld): Abschätzungen des Quadraturfehlers für
Konturintegrale und ihre Anwendung auf die inverse Laplacetransformation
2015/06/01, 16:15, V5-148, AG Dynamische Systeme
Abstract: Zur numerischen Lösung von parabolischen Gleichungen wurden
exponentielle Integratoren vorgestellt, die sich durch inverse
Laplacetransformation auswerten lassen. Diese inversen
Laplacetransformationen sind Konturintegrale, welche durch
Quadraturformeln approximiert werden. Ziel des Vortrages ist es für den
Quadraturfehler dieser Approximationen Abschätzungen zu beweisen, die
die Eigenschaften des Integrationsweges, welcher als Hyperbel gewählt
werden kann, und die sektorielle Eigenschaft des Integranden ausnutzen.
-
Malte Braack (M. Quaas, B. Tews) (Universität Kiel): Fishing strategies as an optimal control problem in multi
dimensions
2015/05/29, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
Marine fisheries are very important to the economy and livelihood of
coastal communities, providing food security and job opportunities. The
preservation of
long-term prosperity and sustainability of marine fisheries is of political
and social significance as well as economical and ecological
importance. Due to new technologies allowing to catch more fish,
various fish stocks like tuna, swordfish, shark, cod,
halibut, etc. have declined by up to 90% in the last decades.
Therefore, some states introduced policy instruments including landing
fees, total allowable catches (TAC's) and marine protect areas (MPA's).
In this context, important social and economical questions arise about
the optimal amount of TAC's as well as the design of those MPA's: What
is the optimal size and location of MPA's with regard to suficient recovery
of the fish stock as well as suficient amount of fisheries yield.
To address to these questions mathematically, the fishing strategy can
be formulated as an optimal control problem.
The fish stock dynamics are modeled by a
time-dependent, non-linear PDE including reproduction and growth
rate. The space-time distributed control describes the fishing
intensity and is assumed to be bilinear with the biomass.
The cost functional takes into account the benefit of the harvest,
fishing costs and the fish stock density at final time which guarantees
sustainability. It turns out that the
optimization problem complemented with additional control constraints
results in a non-standard and non-linear optimal control problem.
This talk is dedicated to the analysis of this problem in terms of
solvability and optimality conditions. We also show first numerical examples.
-
Misha Neklyudov (University of Pisa) : New type of homogenisation problem for stochastic
parabolic equations
2015/04/29, 16:00, D5-153,
Abstract:
We will show that the solution of 1D stochastic parabolic equation with
additive noise converges to a diffusion process independent upon space
variable when we rescale noise at the extremum points of the process. We
will discuss open problems and suggest future directions of research. The
talk is based on a joint work in progress with Ben Goldys.
-
Christian Döding : Realisierung exponentieller Integratoren mittels Laplacetransformation
2015/02/06, 14:15, V5-148, AG Dynamische Systeme
Abstract: Es werden parabolische Differentialgleichungen betrachtet, die sich
als gewöhnliche Differentialgleichungen in einem Banachraum abstrakt schreiben
lassen. Da der auftretende Differentialoperator sektoriell ist,
lassen sich spezielle numerische Verfahren zum Lösen dieser Gleichungen
definieren - die sogenannten exponentiellen Integratoren. Zur Realisierung
dieser Verfahren ist es nötig Funktionen exponentieller Form auf Operatorebene
auszuwerten. Aufgrund der Unbeschränktheit des Differentialoperators scheitert
der Ansatz über Potenzreihen. Vorgestellt wird eine Konturmethode
basierend auf der Laplacetransformation, welche einen Ausweg aus diesem
Problem aufzeigt.
-
Lukasz Targas: Sudoku ist ein NP-vollständiges Problem
2015/02/02, 16:15, V5-148, AG Dynamische Systeme
Abstract: Wir werden die Klasse der NP-vollständigen Probleme
definieren und zeigen, dass das Lösen eines Sudoku-Rätsels zu dieser
Klasse gehört. Dafür werden wir einige graphentheoretische und
kombinatorische Probleme (SAT, 3SAT, 1in3SAT, Triangulation
3-färbbarer Graphen, Vervollständigung lateinischer
Quadrate, Lösung
von Sudoku-Rätsel) ineinander polynomiell transformieren. Die Ideen
der Transformationen werden an zahlreichen Beispielen motiviert.
-
Alina Girod: Erste Einführung in die Theorie zeit-endlicher dynamischer Systeme
2015/01/30, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Die Definitionen für Hyperbolizität, den stabilen und
instabilen Unterraum, sowie für die stabile und instabile
Mannigfaltigkeit eines zeit-unendlichen dynamischen Systems werden
wir auf zeit-endliche Systeme übertragen. Dabei werden wir
feststellen, dass hyperbolische zeit-endliche Systeme keine
eindeutigen Projektoren besitzen. Daher können wir nur
stabile und instabile Kegel definieren, anstatt stabiler und
instabiler Unterräume.
Für diese Kegel leiten wir explizite Darstellungen
her. Anschließend werden wir diese in einem Beispiel betrachten.
-
Evamaria Ruß (Univ. Klagenfurt): Dichotomy Spectrum in Infinite Dimensions
2015/01/19, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The dichotomy spectrum (also known as Sacker-Sell or
dynamical spectrum) is a crucial spectral notion in the theory of
dynamical systems. In this talk we study the dichotomy spectrum in
infinite dimensions. In general we cannot expect a nice structure of
the dichotomy spectrum like in the finite dimensional case, but
compactness properties of the transition operator provide a more
regular spectrum. Finally, we consider applications.
-
Jens Rademacher (Uni Bremen): Pattern formation in simple spintronic device
models with aligned fields
2015/01/12, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The self-organized emergence of spatio-temporal patterns is a ubiquitous phenomenon in nonlinear processes on large homogeneous domains. In this talk a class of Landau-Lifshitz-Gilbert-Slonczewski equations is studied from this viewpoint, highlighting various aspects of the theory. The model describes magnetization dynamics in the presence of an applied field and a spin polarized current. Here we consider the case of axial symmetry and focus on the analysis of coherent structure solutions that occur due to the symmetry. This is joint work with Christof Melcher (RWTH).
-
Robert Haller-Dintelmann (TU Darmstadt): Generalized Ornstein-Uhlenbeck operators in \(L^p\) spaces on domains
2014/12/15, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
We consider the Ornstein-Uhlenbeck operators
\[ A u (x) = \text{div} Q \nabla u(x) + Bx \cdot \nabla u(x)
\]
with suitable matrices \(Q\), \(B\) and a generalized version
\[ A u(x) = \text{div} \mu(x) \nabla u(x) + b(x) \cdot \nabla u(x),
\]
where \(\mu\) is a bounded coeffiecient function and \(b\) is allowed to grow more or less linearly.
We show that these operators, complemented with Dirichlet boundary conditions, are generators of consistent, positive, (quasi-)contractive \(C_0\)-semigroups on \(L^p(\Omega)\) for all \(1 \le p \lt \infty\) and for every domain \(\Omega \subseteq {\mathbb{R}}^d\). In order to do so, we use a generation result in \(L^2(\Omega)\) and derive kernel estimates for this semigroup. In the special case of an exterior domain with sufficiently smooth boundary it is even possible to give a result on the location of the spectrum of Ornstein-Uhlenbeck opperators on domains.
-
Christian Vieth (Bielefeld): Deterministische Fortsetzung von Gleichgewichten
und Konfidenzellipsoiden in stochastischen Differentialgleichungen
2014/12/12, 14:15, V5-148, AG Dynamische Systeme
-
Fabian Wirth (Univ. Passau): Stabilisierbarkeit linearer zeitvarianter Systeme
2014/12/8, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Wir betrachten lineare zeitvariante Kontrollsysteme in stetiger Zeit und
untersuchen die Frage, unter welchen Bedingungen stabilisierende
Rückkopplungen existieren.
Im zeitinvarianten Fall ist dieses Problem seit langem
geklärt. Kontrollierbarkeit ist äquivalent zu der Eigenschaft, dass
beliebige Eigenwerte durch Rückkopplung vorgegeben werden
können. Das
System ist stabilisierbar, wenn der instabile Unterraum des freien
Systems im kontrollierbaren Unterraum enthalten ist.
Für zeitvariante Systeme werden die entsprechenden Fragestellungen
feiner, schon weil die Stabilitätsbegriffe gleichmäßige exponentielle
Stabilität, exponentielle Stabilität und asymptotische
Stabilität
auseinander fallen. Zur Charakterisierung der verschiedenen
Stabilitätseigenschaften werden Bohl- und Lyapunovexponenten verwendet,
und die Frage ist dann, welche Bohl- oder Lyapunovexponenten durch
Rückkopplung erreichbar sind.
Im Vortrag wird der Zusammenhang zwischen (gleichmäßiger)
exponentieller Stabilisierbarkeit und (gleichmäßiger) Kontrollierbarkeit
diskutiert und es werden Methoden aus der optimalen Steuerung
vorgestellt, mit deren Hilfe die entsprechenden Aussagen bewiesen werden
können. Diese Methoden liefern außerdem ein Kriterium für die
Stabilisierbarkeit zeitvarianter Systeme.
-
Tomas Dohnal (Uni Dortmund):
2014/12/01, 16:15, V5--148, Seminar Numerical Analysis
Abstract: In periodic media, e.g., photonic crystals, the quest for moving localized pulses with profiles that are close to constant or periodic in time is interesting from a mathematical as well as an applied point of view. In optical computing such pulses would be versatile bit carriers. We seek them for frequencies in spectral gaps (so called band gaps) of the spatial operator and call them \textit{gap solitons}.
Asymptotically near spectral edges gap solitons can be approximated as linear carrier waves modulated by slowly varying envelopes, which satisfy effective nonlinear amplitude equations. The carrier waves need to have a nonzero group velocity to guarantee movement of the gap soliton. Moving gap solitons have been previously studied only in structures with asymptotically small contrast of the periodicity because in finite contrast structures the group velocity of the corresponding carrier waves is generically zero. In 1D for perturbations of, so called, \textit{finite band periodic potentials} this is, however, violated and moving gap solitons are possible.
Starting with the 1D peri odic nonlinear Schrödinger equation
\[{\rm i}\partial_t u +\Delta u-V(x) u -\sigma |u|^2 u =0, \quad x\in \mathbb{R},
\]
we present a derivation of the corresponding effective envelope equations and a technique to obtain localized solutions of these. We present numerical examples and discuss the current project on a rigorous justification of the effective equations.
-
Hannes Uecker (Univ. Oldenburg) : Generic Bifurcation of Nonlinear Bloch Waves from
the Spectrum in the Gross-Pitaevskii Equation
2014/11/24, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We rigorously analyze the bifurcation of so called
nonlinear Bloch waves (NLBs) from the spectrum in the Gross-Pitaevskii
(GP) equation with a periodic potential, in arbitrary space dimensions.
These are solutions which can be expressed as finite sums of
quasi-periodic functions, and which in a formal asymptotic expansion
are obtained from solutions of the so-called
algebraic coupled mode equations. Here we justify this expansion
by proving the existence of NLBs and estimating the error
of the formal asymptotics. The analysis is illustrated by numerical
bifurcation diagrams, mostly in 2D, and we also illustrate some
relations to other classes of solutions of the GP equation, in
particular to so called out--of--gap solitons and truncated NLBs.
Das verbindet sozusagen Analysis für wave-trains mit Illustration via
pde2path.
-
Sören Bartels (Uni Freiburg): Finite element approximation of functions of
bounded variation
2014/11/17, 15:00!, U0-131!, Seminar Numerical Analysis
Abstract:
Various phenomena involving free boundaries such as damage or plasticity
require the description of physical quantities with discontinuous
functions. One approach to their mathematical modeling is based on the
space of functions of bounded variation which includes functions that
are discontinuous and may jump across lower dimensional subsets.
Numerical methods for their approximate solution are often based on
regularizations which typically lead to restrictive conditions on
discretization parameters. We try to avoid such modifications and
discuss the convergence of discretizations with different finite element
spaces, the iterative solution of the resulting finite-dimensional
nonlinear systems of equations, and adaptive mesh-refinement techniques
based on rigorous a~posteriori error estimates for a model problem
related to image processing. The application of the techniques to total
variation flow, very singular diffusion processes, and segmentation
problems will be addressed. Part of this talk is based on joint work
with Ricardo H. Nochetto (University of Maryland, USA) and Abner J.
Salgado (University of Maryland, USA).
-
Achim Schädle (Univ. Düsseldorf) : Transparent boundary conditions ---
On the relationship between the pole condition, absorbing
boundary conditions and perfectly matched layers
2014/11/10, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Transparent (or exact or non-reflecting) boundary conditions are
employed to truncate infinite computational domains. They are usually
non-local and expensive to evaluate.
In this talk approximate cheap boundary condition for the
Schr"odinger, the Klein-Gordon and the Helmholtz equation
are derived based on the pole condition.
We show that for the simplest model problem, the Helmholtz equation on an
infinite strip, a certain discretization of the pole condition
can be interpreted both as a high order absorbing boundary condition
and a perfectly matched layer, two other well known methods to
approximate a transparent boundary condition.
-
Etienne Emmrich (TU Berlin) : The peridynamic model in nonlocal elasticity theory
2014/10/27, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Peridynamics is a nonlocal continuum theory which avoids any spatial
derivative. It is believed to be suited for the description of fracture and
other material
failure, and to model multiscale problems. In this talk, we introduce the
peridynamic model and discuss several aspects of its mathematical analysis. We
review recent results on the existence of solutions to the peridynamic equation
of motion for a large class of nonlinear pairwise force functions modeling
isotropic microelastic material. Our method of proof applies also to other
nonlocal evolution equations.
This is joint work with Dimitri Puhst (Berlin).
-
Stefanie Hittmeyer (University of Auckland) : Bifurcations of invariant sets in a map model of wild chaos
2014/10/24, 15:00, V5-148, Seminar Numerical Analysis
Abstract: We study a two-dimensional noninvertible map that has been introduced
by Bamon, Kiwi and Rivera in 2006 as a model of wild Lorenz-like chaos. The map
acts on the plane by opening up the critical point to a disk and wrapping the
plane twice around it; points inside the disk have no preimage. The bounding
critical circle and its images, together with the critical point and its
preimages, form the so-called critical set. This set interacts with the stable
and unstable sets of a saddle fixed point and other saddle invariant sets.
Advanced numerical techniques enable us to study how these invariant sets
change as the parameters are varied towards the wild chaotic regime. We find a
consistent sequence of four types of bifurcations, which we present as a first
attempt towards explaining the geometric nature of wild chaos. In a different
parameter regime, the map acts as a perturbation of the complex quadratic
family and admits (a generalised notion of) the Julia set as an additional
invariant set. When parameters are varied, this set interacts with the other
invariant sets, leading to the (dis)appearance of saddle points and chaotic
attractors and to dramatic changes in the topology of the Julia set. In
particular, we find generalised Julia sets in the form of Cantor bouquets,
Cantor tangles and Cantor cheeses. Using two-parameter bifurcation diagrams, we
obtain an indication on the size of the parameter region where wild chaos is
conjectured to exist and reveal a self-similar bifurcation structure near the
period-doubling route to chaos in the complex quadratic family.
-
Raphael Kruse (TU Berlin) : A new approach to the weak error analysis for
SDEs with multiplicative noise
2014/06/23, 16:15, V5-148, Seminar Numerical Analysis
-
Joseph N. Paez (TU Dresden): Mathematical Modelling and Experimental Study
of Engineering Systems: Applications to Oil-Well Drilling.
2014/06/13, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this presentation we will describe a number of research
projects carried out at the Centre for Applied Dynamics Research (CADR),
Aberdeen University (United Kingdom). The topics to be covered are: Drifting
Oscillators, Impacting Systems, Drill-String Vibrations and Rotor Dynamics.
For all these investigations, a particular problem related to the Oil and
Gas Industry has been considered. A crucial step in this research is the
construction of suitable mathematical models capable of reproducing
quantitative- or qualitatively the dynamic behavior observed via
experimental measurements. All the models in question involve
piecewise-smooth ODEs. In addition, a detailed bifurcation analysis of the
models is carried out, for which we use the software package TC-HAT, an Auto
97 toolbox for the numerical continuation of periodic orbits of non-smooth
systems.
-
Alina Girod : Homoclinic trajectories in non-autonomous systems and their discretization
2014/06/06, 14:15, V5-148, AG Dynamische Systeme
Abstract:
We consider a continuous time non-autonomous dynamical system having
two hyperbolic bounded trajectories that converge towards each other.
Applying a one-step-method with sufficiently small step size we
get hyperbolic bounded trajectories of the discretized system.
They lie in a small neighborhood of the original trajectories and
are also homoclinic.
For verifying our error estimates, we construct an example in
continuous time with known homoclinic trajectories.
An illustration of homoclinic dynamics can be achieved by
computing stable and unstable fiber bundles.
For this task, an algorithm of England, Krauskopf and Osinga
is introduced that we generalize to the non-autonomous case.
-
Torsten Buschmann : Modellgleichungen für Chemotaxis
2014/05/30, 14:15, V5-148, AG Dynamische Systeme
-
Michael Hinze (Univ. Hamburg): Simulation and model predictive control of two-phase
flows with variable density
2014/05/19, 14:15, T2-234, Seminar Numerical Analysis
Abstract: We present a fully practical residual-based adaptive
simulation framework for two-phase flows with variable densities
governed by a Cahn-Hilliard Navier-Stokes model with double obstacle
potential. In particular we present a new stable time integration
scheme. Moreover, we consider wall parallel Dirichlet boundary control
of the flow part to achieve a prescribed concentration field. We present
a recipe how to construct the underlying controller and how to achieve
his stabilizing properties.
This is joint work with Harald Garcke, Michael Hintermüller and
Christian Kahle.
-
Thorsten Hohage (Univ. Göttingen): Hardy Space Infinite Elements for Waves with
Different signs of Group and Phase Velocities
2014/04/28, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We consider time harmonic wave equations in cylindric waveguides
with physical solutions for which the signs of group and phase velocities
differ. In particular, we will consider a one-dimensional fourth order
model problem and two-dimensional elastic waveguides for which this
phenomenon occurs. Standard transparent boundary conditions, e.g. the
Perfectly Matched Layers (PML) method select modes with positive phase
velocity, whereas physical modes are characterized by positive group
velocity.
Hence these methods yield stable, but unphysical solutions for such
problems.
We derive an infinite element method for a physically correct
discretization of such waveguide problems which is based on a Laplace
transform in propagation direction. In the Laplace domain the space of
transformed solutions can be separated into a sum of a space of
incoming and a space of
outgoing functions where both function spaces are curved Hardy spaces.
The curved Hardy space is constructed such that it contains a simple and
convenient Riesz basis with moderate condition numbers. Our method does not
use a modal separation and works on an interval of frequencies. In
particular, it is well-adapted for the computation of resonances.
Numerical experiments exhibit super-algebraic convergence and moderate
condition numbers.
-
Georgy Kitavtsev (Max-Planck-Institut Leipzig): Stable FEM discretizations for a certain class of
lubrication, shallow water and Korteweg systems'.
2014/02/10, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
In this talk we discuss existence of weak solutions and corresponding
stable FEM discretizations for a certain class of PDEs that include some
known lubrication, shallow water and Korteweg systems. A common feature of
these systems and at the same time a challenge for their consideration is
that the viscosity terms degenerate as the solution for density/height
approaches zero. As a related consequence to this fact it was observed
that these systems dissipate besides a classical energy functional a so
call Bresch and Desjardins entropy one which provides a higher regularity for
the density/height solution. Regularized systems and their FEM
discretization possessing the same dissipative properties as the original
ones will be presented and analyzed.
-
Andreas Prohl (Univ. Tübingen): Strong convergence with rates for discretizations
of SPDEs with non-Lipschitz drift
2014/02/06, 14:15, V5-148, AG Dynamische Systeme
Abstract:
I discuss the convergence analysis for
space-time discretizations of three nonlinear SPDE's:
the stochastic Navier-Stokes equation, the stochastic
Allen-Cahn equation, and the stochastic mean curvature
flow of planar curves of graphs. Depending on the drift
operator, optimal rates w.r.t. strong convergence are
valid for errors on large subsets, or on the whole sample set.
-
Roland Schnaubelt (TU Karlsruhe): Splittingmethoden für
Schrödingergleichungen mit singulären Potentialen
2014/01/22, 16:15, V5-148, Seminar Numerical Analysis
-
Andre Schenke : Der Satz von Smale für nichtinvertierbare Systeme
2014/01/17, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Der Satz von Smale impliziert eine chaotische Dynamik in der Nähe eines
transversalen homoklinen Orbits, welcher von einem Diffeomorphismus
erzeugt wird.
Wir geben einen Beweis einer Version des Satzes von Smale im
nichtinvertierbaren Fall. Grundlage hierfür ist eine Arbeit von Beyn,
welche auf einer Idee von Palmer beruht. Wichtigstes Hilfsmittel ist
eine nichtinvertierbare Version des Shadowing-Lemmas.
-
Misha Neklyudov (University of Sydney): Dynamics of nanomagnetic particle systems
2014/01/13, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
The dynamics of nanomagnetic particles is described by the
stochastic Landau-Lifshitz-Gilbert (SLLG) equation.
In the first part of the talk we will discuss the long time behaviour of the finite-dimensional SLLG equation. Firstly, we explain how statistical mechanics argument defines the form of the noise of the equation. Then we will consider different approximations of the equation such as structure preserving discretisation and penalisation approximation. We discuss the convergence of approximations andtheir consistency with the long time behaviour of the system.
In the second part of the talk we will look at the infinite dimensional case. Firstly, we present a numerical scheme convergent to the solution of SLLG equation. Then we show some numerical results and discuss open problems, such as existence of invariant measure, existence of solution in the case of space-time white noise, etc. In particular we will explain why Krylov-Bogoliubov Theorem is not directly applicable to the proof of existence of invariant measure even in the case of coloured noise. In the end we will present certain transformation of SLLG equation which allows to represent the noise as the sum of additive noise and energy conservative noise.
Computational examples will be reported to illustrate the theory.
The talk is based on the recently published book (jointly with
L. Banas, Z. Brzezniak, A. Prohl) and on the work in progress of the author.
-
Marc Winter : Taylor-Approximation invarianter Faserbündel (Part 2)
2014/01/10, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten eine nicht-autonome Differenzengleichung der Form
\(x(n+1)=A(n)x(n)+F(x(n),n)\), \(n \in \mathbb{Z}\).
Wir definieren die lokalen und globalen invarianten Faserbündel
der Differenzengleichung als Analogon zu den Mannigfaltigkeiten
autonomer Differenzengleichungen.
Im ersten Vortrag haben wir untersucht, unter welchen Voraussetzungen
diese Faserbündel existieren.
Anschließend haben wir gesehen, wie wir diese Faserbündel
mit Hilfe der Taylorentwicklung approximieren können.
In diesem Vortrag werden wir die Ergebnisse einer
Matlab-Implementation dieses Approximationsverfahrens betrachten.
Wir werden das Verfahren auf eine spezielle Klasse von Funktionen
anwenden, welche ein Polynom als Faserbündel besitzen,
sowie auf die Hénon-Abbildung.
-
Elena Isaak (Bielefeld) : Numerical analysis of the balanced Milstein method
2013/12/13, 14:15, V5-148, AG Dynamische Systeme
Abstract: Balanced Milstein methods (BMM) have been proposed for
solving numerically stochastic ordinary differential
equations with large noise coefficients.
In this talk we discuss consistency, bistability and convergence of the BMM.
The main ingredient of the analysis is a stochastic version of Spijker's
norm. We show that the order of consistency for the BMM in this norm is one,
and we prove bistability which leads to two-sided estimates of the strong
error of convergence.
-
Kathrin Glau (TU München): Kolmogorov backward equations for option pricing
in Lévy models
2013/12/09, 16:00, V5-148, Seminar Numerical Analysis
Abstract: One major task mathematical finance sets itself is modeling, pricing and calibration of financial instruments. (Semi)martingale theory is used for modeling and derivative prices are written as conditional expectations. Typically, the latter are not available in closed form and, thus, computational methods become necessary. Essentially three approaches to compute the expectations are being used: Monte Carlo simulation, Fourier based valuation methods and the representation of prices as solutions of partial integro-differential equations (PIDEs). In this context we focus on Galerkin methods for solving PIDEs arising in Lévy models. We classify Lévy processes according to the solution spaces of the associated parabolic PIDEs and point out the role of the symbol. Furthermore, we derive Feynman-Kac representations of variational solutions. We discuss applications to option pricing and give an outlook on a Finite Element solver based on the symbol.
-
L´ubomír Banas (Bielefeld): Phase field models for multiphase flow:
modelling, numerics and applications.
2013/12/02, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Understanding and accurate prediction of multiphase multicomponent flows
is of essential interest for a large number of
scientific and engineering applications. Despite intensive past and
present research efforts, it is still not clear how to accurately
and efficiently simulate multiphase fluid flow for the full range of
physical parameters and regimes such as, e.g., densities,
viscosities, capillary relations, number of fluid phases, interface
geometry, dynamic or static contact angles, etc.
We review of a promising strategy for the modelling of incompressible
multiphase flow based on the phase-field approach.
We discuss advantages of the approach from the modelling and computational
point of view. We also present a framework
for multiscale flow simulations and discuss applications to multiphase
flow in porous media.
-
Marian Slodicka (Gent): Inverse source problems in parabolic equations
2013/11/29, 14:15, V5-148, AG Dynamische Systeme
Abstract: Inverse coefficient and source problems for partial
differential equations represent a well-known and established area of mathematical research in the last decades.
They appear in various applied technologies (geophysics, optic, tomography, remote sensing, radar-location, etc.).
Inverse source problems for evolutionary (parabolic, hyperbolic, Navier-Stokes) settings have been intensively studied
by many authors.
We study a problem of source identification from given data for the
parabolic heat equation in several dimensions. The temperature \(u\), heat source \(F\) and the initial
temperature distribution \(u_0(x)\) then satisfy
\[\partial_tu + A u = F in\ \ \Omega\times (0,T),\]
\[u(x,0) = u_0(x) for\ \ x\in \Omega\]
along with appropriate boundary conditions. Here, \(A\) is a strongly
elliptic, linear differential operator of
second-order.
The right-hand side \(F\) is assumed to be separable in both variables \(x\) and \(t\), i.e.
\[F(x,t)=g(x)h(t).\]
Two kinds of inverse problems will be addressed:
-- reconstructing the source \(g(x)\) (when \(h(t)\) is given)
from the additional information \(u(x,T) = \psi_T(x)\quad\mbox{for}\ \ x\in \Omega\)
-- identification of the unknown function \(h(t)\) from additional data, assuming that \(g(x)\) is known.
The unknown function \(h(t)\) is then recovered from a single point
measurement \(u(y,t),\ t\in\ I\) at a given point \(y\in\overline\Omega\).
-
Ludwig Gauckler (TU Berlin): Mathematical and numerical analysis of
Hamiltonian partial differential equations on long time intervals
2013/11/25, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Qualitative properties of Hamiltonian partial differential
equations on long time intervals are to be discussed in the talk, and the
preservation of these properties by a numerical discretization will be
studied. In the first part of the talk we will discuss for some numerical
methods the long-time near-conservation of the energy, an important
conserved quantity of these equations. In the second part of the talk we
will study the long-time stability of plane wave solutions to the nonlinear
Schrödinger equation, first for the exact solution and then for the
numerical discretization of the equation by the popular split-step Fourier
method.
-
Sebastian Paul : Ein endliches Kriterium zur Transversalität homokliner Orbits
2013/11/22, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Ziel des Vortrags ist ein numerisches Verfahren,
mit dem wir homokline Orbits eines diskreten, autonomen dynamischen
Systems auf Transversalität prüfen können.
Unter Verwendung des im ersten Vortrag bewiesenen Satzes reicht
es dazu aus, eine exponentielle Dichotomie der Variationsgleichung
auf einem hinreichend großen, endlichen Intervall
\([-T,T], T \in \mathbb{N}\) nachzuweisen.
Im Anschluss daran werden wir die Ergebnisse anhand
der Hénon-Abbildung illustrieren.
-
Zdzislaw Brzezniak (York): Stochastic Euler equations in unbounded 2-D domains
2013/11/18, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
I will speak about the existence of a martingale solution to
stochastic Euler Equations (with general multiplicative noise) in the
Sobolev \(H^{1,q}\cap H^{1,2}\) spaces (based on a 2001 paper with
Peszat) and about the existence and uniquence of solutions with
bounded vorticity for a specila multiplicative noise (based on a
recent unfished work with Flandoli and Maurielli). Somce comments
about the existence to stochastic NSEs in unboded domains (based on a
work with E. Motyl) wil also be made.
-
Simon Pelster : Spektren kontinuierlicher Dynamischer Systeme
2013/11/15, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Der Vortrag stellt das Ljapunow-Spektrum und das berechnete
Ljapunow-Spektrum für diskrete dynamische Systeme der Form
\(u_{t+1}=A_t u_t\)
vor. Es wird bewiesen, dass die Ljapunow-Exponenten für Systeme
mit \(\sup_{t\in \mathbb{Z}} \|A_t\|=M < \infty\) endlich sind.
Außerdem wird ein Kriterium,
das die Äquivalenz der beiden Spektren im diskreten Fall liefert,
präsentiert.
-
Andrea Lunari (Bielefeld): Optimal Control for a Phase-Field Model of Multiphase Flow
2013/11/11, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
The optimal control of a multiphase flow is a very interesting and challenging
subject from the analytical point of view and leads to concrete industrial
applications (e.g. binary alloy, polymer fluids).
In this talk I discuss the optimal control of a two-phase fluid flow described
by a coupled Cahn-Hilliard-Stokes system, showing the mathematical settings for
the problem and its features from an analytical point of view.
Then I present a space-time dicretization and an algorithm for the solution of
the associated discrete optimal control problem. Finally, I show some first
numerical experiments.
-
Adam Andersson (Göteborg): A new approach to weak convergence of SPDEs
2013/11/08, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Weak convergence of numerical approximations for non-linear SPDEs has
previously been proved by a use of the Itô formula and the Kolmogorov
equation. In this talk I will present a new method to prove weak
convergence for semilinear equations with additive noise, not relying
neither on the Itô formula nor on the Kolmogorov equation. We linearize the
weak error and obtain a remainder term with high order of convergence. For
the linearized term we use the fact that the gradient of the test function,
evaluated at the solution of the SPDE, is a Malliavin smooth random
variable. This allows us to estimate this term by taking the supremum over
a bounded subset of random variables from the Malliavin space. After some
analysis a use of the Gronwall Lemma is possible. The order of weak
convergence, is as expected, twice that of strong convergence.
The novelty this result, except for being a new method of proof, is that it
allows for test functions with polynomial growth, meaning that we have
proved convergence of any moment. This is joint work with Raphael Kruse
(ETH) and Stig Larsson (Chalmers).
-
Gerhard Unger (TU Graz): Boundary element methods for eigenvalue problems
in acoustics
2013/10/28, 16:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we present an overview about boundary element methods for
eigenvalue problems in acoustics. Our approach is based on
a reduction of eigenvalue problems to the boundary of the considered domain.
Therefore boundary element methods are in particular suitable for problems
which
are posed in unbounded domains. Boundary integral formulations of eigenvalue
problems lead to nonlinear eigenvalue problems even if the original
eigenvalue
problem is a linear one. The reason for that is that the eigenvalue
parameter
occurs nonlinearly in the fundamental solution which is related to the
underlying partial differential equation. The used boundary integral
formulations for the eigenvalue problems can be considered as eigenvalue
problems for holomorphic Fredholm operator-valued functions for which a
comprehensive theory is well-established. Within this theory convergence
results
for the Galerkin discretization of boundary integral formulations of
eigenvalue
problems are derived. For the numerical solution of the discretized
eigenvalue
problems the contour integral method is applied. We present several
numerical
examples of acoustic and vibro-acoustic eigenvalue problems which
demonstrate
the feasibility of our approach.
-
Koray Arslan : Energieerhaltende Integratoren für Poisson Systeme
2013/07/22, 16:00, V5-148, Seminar Numerical Analysis
Abstract:
Mit den sogenannten Poisson Systemen betrachten wir in diesem
Vortrag nicht-kanonische Hamiltonsche Systeme und zeigen, dass jede
Erhaltungsgröße dieses Systems - insbesondere die Hamiltonsche und die
Casimir Funktion - entlang der exakten Lösung erhalten bleibt.
Wir stellen anschließend eine neue Klasse von numerischen Verfahren vor, die
von E. Hairer & D. Cohen 2011 eigens für Poisson Systeme entwickelt wurde.
Wir zeigen, dass diese Verfahren die Hamiltonsche Funktion und quadratische
Casimir Funktionen erhalten und dass sie invariant unter linearen
Transformationen sind.
-
Marc Winter: Taylor-Approximation invarianter Faserbündel
2013/07/19, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten eine nicht-autonome Differenzengleichung der
Form \(x(n+1)=A(n)x(n)+F(x(n),n)\), \(n \in \mathbb{Z}\).
Wir definieren die lokalen und globalen invarianten Faserbündel
der Differenzengleichung als Analogon zu den Mannigfaltigkeiten
autonomer Differenzengleichungen.
Dann untersuchen wir, unter welchen Voraussetzungen diese
Faserbündel existieren.
Anschließend werden wir diese Faserbündel mit Hilfe der
Taylorentwicklung approximieren.
-
Jessica Jandulski : Das Sharkovskii-Theorem für periodische Differenzengleichungen - Part 2
2013/07/15, 16:00, V5-148, AG Dynamische Systeme
Abstract:
Während des ersten Vortrags lernten wir das folgende
Sharkovskii-Theorem für periodische Differenzengleichungen kennen:
Sei \(f_{n\mod p}(x_n)=x_{n+1}\), \(n\in\mathbb{N}\), \(f_n\in C(I,I)\)
für alle \(n\in\mathbb{N}\) eine \(p\)-periodische
Differenzengleichung, die einen minimalen \(r\)-Zyklus
mit \(r\in A_{p,l}\) hat.
Dann hat die Differenzengleichung für alle \(A_{p,q}\)
mit \(A_{p,l}>A_{p,q}\) in der \(p\)-Sharkovskii-Ordnung
einen minimalen \(k\)-Zyklus mit \(k\in A_{p,q}\).
Ziel des zweiten Vortrags wird es sein, das nicht-autonome System
unter Verwendung des Konzepts der Schiefprodukt-Flüsse in ein
autonomes System zu überführen und dann das
Theorem mithilfe des klassischen Sharkovskii-Theorems zu beweisen.
-
Martin Rasmussen (Imperial College London) : Bifurcations of random dynamical systems
2013/07/08, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Despite its importance for applications, relatively little
progress has been made towards the development of a bifurcation theory for
random dynamical systems. In this talk, I will demonstrate that adding noise
to a deterministic mapping with a pitchfork bifurcation does not destroy the
bifurcation, but leads to two different types of bifurcations. The first
bifurcation is characterized by a breakdown of uniform attraction, while the
second bifurcation can be described topologically. Both bifurcations do not
correspond to a change of sign of the Lyapunov exponents, but I will explain
that these bifurcations can be characterized by qualitative changes in the
dichotomy spectrum and collisions of attractor-repeller pairs.
This is joint work with M. Callaway, T.S. Doan, J.S.W Lamb (Imperial
College) and C.S. Rodrigues (MPI Leipzig)
-
Raphael Kruse (ETH Zürich): Konsistenz und Stabilität von Galerkin
finite Elemente Methoden für
Reaktions-Diffusions-Gleichungen
2013/07/01, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Wir betrachten Galerkin finite Elemente Methoden für
(deterministische) semilineare Reaktions-Diffusions-Gleichungen
und betten diese in den abstrakten Rahmen der diskreten
Approximationstheorie ein. Basierend auf einer passend für
Halbgruppen verallgemeinerten Spijker Norm beweisen wir die
Bistabilität des Verfahrens und leiten zweiseitige
Fehlerabschätzungen her. Anschließend vervollständigen
wir den Konvergenzbeweis mit einer Analyse des Konsistenzfehlers.
-
Paul Voigt (Bielefeld): Das Dirichletproblem für nicht-lokale nicht-symmetrische Operatoren
2013/06/28, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Im Vortrag wird das elliptische Dirichletproblem für lineare nicht-lokale
und nicht notwendigerweise symmetrische Operatoren studiert.
Aufgrund der Nicht-lokalität des Operators werden die
Randdaten - im Gegensatz zum klassischen Dirichletproblem - auf
dem Komplement einer gegebenen Menge vorgegeben.
Das Problem wird in einem klassischen Hilbertraum-Setting formuliert.
Existenz und Eindeutigkeit von Lösungen wird
mit Standardtechniken, wie z.B. der Fredholm-Alternative bewiesen.
-
Alina Girod: Diskretisierung homokliner Orbits im nicht-autonomen Fall
2013/06/24, 16:00, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten ein kontinuierliches nicht-autonomes Dynamisches System,
welches einen transversalen homoklinen Orbit besitzt.
Dieses diskretisieren wir zunächst exakt. Diskretisieren wir mit
einem Einschritt-Verfahren, welches nah am exakt
diskretisierten System ist, so erhalten wir wieder einen
transversalen Orbit der nah an dem exakt diskretisierten Orbit liegt.
Anschließend werden wir die Theorie an einem Beispiel illustrieren.
-
Robin Flohr : Konvergenz des Strang-Operatorsplittings - Part 2
2013/06/14, 14:15, V5-148, AG Dynamische Systeme
-
Robin Flohr : Konvergenz des Strang-Operatorsplittings
2013/06/14, 14:15, V5-148, AG Dynamische Systeme
Abstract:
In dem Vortrag wird das Prinzip des Operatorsplittings
von Gleichungen der Form \(u_t = Au + uu_x\) vorgestellt.
\(A\) ist dabei ein linearer Differentialoperator,
so dass die Gleichung wohlgestellt ist.
Wichtige Beispiele für \(A\) sind dabei \(Au=u_{xx}\)
oder \(A=u_{xxx}\), so
dass die Theorie sowohl für die Burgers-Gleichung als auch
für die KdV-Gleichung anwendbar ist.
Außerdem werden Regularitätsaussagen der
getrennten Probleme sowie die Konvergenz erster Ordnung
des Strang-Splittings bewiesen.
-
Jessica Jandulski : Das Sharkovskii-Theorem für periodische Differenzengleichungen
2013/06/03, 16:00, V5-148, AG Dynamische Systeme
Abstract:
Das Sharkovskii-Theorem für autonome Differenzengleichungen behandelt
eine stetige, reellwertige Abbildung \(f\),
die einen periodischen Orbit der minimalen Periode \(n\)
besitzt und liefert die Antwort auf die Frage:
Für welche \(m\) existieren dann auch \(m\)-periodische Orbits?
Unser Ziel wird es sein, das Sharkovskii-Theorem auf
\(p\)-periodische Differenzengleichungen
\(x_{n+1}=f_{n\mod p}(x_n)\) zu erweitern.
Dafür lernen wir zunächst einen Spezialfall kennen,
den wir mithilfe des klassischen Sharkovskii-Theorems beweisen.
Anschließend betrachten wir das allgemeinere Sharkovskii-Theorem
für \(p\)-periodische Differenzengleichungen
und beweisen auch dieses Theorem unter Verwendung des
Konzepts der Schiefprodukt-Flüsse mithilfe
des klassischen Sharkovskii-Theorems.
-
Sebastian Paul : Dichotomien im Übergang von endlichen zu unendlichen Intervallen
2013/05/31, 14:15, V5-148, AG Dynamische Systeme
Abstract:
In diesem Vortrag gehen wir zunächst von einer
exponentiellen Dichotomie auf endlichen Intervallen aus.
Unter welchen Voraussetzungen lässt sich daraus eine
exponentielle Dichotomie auf \(\mathbb{Z}\) zusammensetzen?
Wir liefern Bedingungen, unter denen dies möglich ist
und beweisen diese Aussage mit Hilfe des Roughness-Theorems.
-
Rudolf Dürksen : Oberhalbstetigkeit von Pullback-Attraktoren
2013/05/27, 16:00, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten die nichtautonome Differentialgleichung
\(\dot{x}=f(x,t),\ x(s)=x_s\),
wobei \(f\in C(\mathbb{R}^p\times\mathbb{R},\mathbb{R}^p)\).
Im nichtautonomen Fall sind die Lösungen sowohl von der
Endzeit \(t\), als auch von der Startzeit \(s\) explizit abhängig,
wohingegen im autonomen Fall nur die bereits verstrichene
Zeit \(t-s\) relevant ist. In diesem Zusammenhang werden wir
den Begriff der Pullback-Konvergenz einführen und einen für
nichtautonome Systeme geeigneten Attraktor, den sogenannten
Pullback-Attraktor, definieren. Ziel des Vortrags ist es,
zu sehen, dass auch der Pullback-Attraktor
unter gewissen Voraussetzungen oberhalbstetig ist.
-
Wolf-Jürgen Beyn (Bielefeld): Mathematische Modellbildung, Analyse und Simulation
zellulärer Prozesse
2013/05/24, 16:15, V5-148,
Abstract: Im Vortrag werden einige Grundprinzipien mathematischer
Modellbildung diskutiert, die zum Verständnis des Zusammenwirkens
zellulärer Einzelprozesse beitragen können.
Zunächst wird auf die verschiedenen Modelltypen eingegangen,
die sich durch Begriffspaare wie diskret-kontinuierlich,
stationär-zeitabhängig, räumlich homogen-inhomogen,
linear-nichtlinear und
zufällig-deterministisch unterscheiden lassen.
Speziell werden dann einfache Modellgleichungen für enzymatisch
ablaufende Stoffwechselprozesse analysiert und Möglichkeiten
aufgezeigt, um diese Modelle auf Transportprozesse
und genetische regulierte Netzwerke zu erweitern.
Dabei entstehen oft große Systeme nichtlinearer Differentialgleichungen,
die eine Vielzahl von Parametern enthalten und deren Lösungsverhalten
nicht einfach zu überblicken ist. Einerseits werden solche Systeme
auf dem Computer simuliert und mit experimentellen Daten verglichen,
andererseits versucht man die Modelle so zu reduzieren
(Hauptkomponentenanalyse, Pseudostationarität), dass Einsichten in
biochemisch relevantes Verhalten gewonnen werden können.
-
Simon Pelster : Spektren kontinuierlicher Dynamischer Systeme
2013/05/24, 14:00, V5-148, AG Dynamische Systeme
Abstract:
Der Vortrag stellt das Ljapunow-Spektrum und das berechnete
Ljapunow-Spektrum kontinuierlicher dynamischer Systeme vor.
Unter der Voraussetzung integraler Getrenntheit sind die
Spektren für Systeme mit oberer Dreiecksgestalt identisch.
Im zweiten Teil wird die Verbindung vom berechneten
Ljapunow-Spektrum zum Sacker-Sell-Spektrum
für kontinuierliche Systeme hergestellt.
-
Koray Arslan
: Symplektizität in numerischen Verfahren und
Beispiele symplektischer Integratoren
2013/05/17, 14:15, V5-148, AG Dynamische Systeme
Abstract: Nachdem in der ersten Vortragsreihe der Begriff der
Symplektizität eingeführt und im Satz von Poincaré gezeigt
wurde, dass der
exakte Fluss eines Hamiltonschen Systems symplektisch ist, werden wir nun
numerische Verfahren konstruieren, von denen wir auch fordern, dass deren
diskreter Fluss symplektisch ist.
Dazu definieren wir erst, was ein symplektisches Verfahren ist, und
untersuchen anschließend verschiedene numerische Verfahren auf ihre
Symplektizität.
Dabei richtet sich unser Hauptaugenmerk auf Runge-Kutta-Verfahren,
die - wie aus der Numerik II bekannt ist - eine wichtige Klasse von
Einschrittverfahren für Anfangswertaufgaben bilden.
-
Koray Arslan: Symplektizität in numerischen Verfahren und
Beispiele symplektischer Integratoren
2013/05/13, 16:00, V5-148, AG Dynamische Systeme
Abstract: Nachdem in der ersten Vortragsreihe der Begriff der
Symplektizität eingeführt und im Satz von Poincaré gezeigt
wurde, dass der
exakte Fluss eines Hamiltonschen Systems symplektisch ist, werden wir nun
numerische Verfahren konstruieren, von denen wir auch fordern, dass deren
diskreter Fluss symplektisch ist.
Dazu definieren wir erst, was ein symplektisches Verfahren ist, und
untersuchen anschließend verschiedene numerische Verfahren auf ihre
Symplektizität.
Dabei richtet sich unser Hauptaugenmerk auf Runge-Kutta-Verfahren,
die - wie aus der Numerik II bekannt ist - eine wichtige Klasse von
Einschrittverfahren für Anfangswertaufgaben bilden.
-
Andre Schenke: Exponentielle Dichotomien für nichtinvertierbare
Systeme - Part 2
2013/05/10, 14:15, V5-148, AG Dynamische Systeme
-
David Kiesewalter: Die Randelementmethode für das
Eigenwertproblem zum Laplaceoprator
2013/05/06, 16:00, V5-148, AG Dynamische Systeme
-
Abderrahman Boukricha (Tunis): Variational Formulation of Nonlocal and
Quasilinear Elliptic Problems and Numerical Analysis of the
Weighted p-Laplacian
2013/04/26, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
The principle of variational formulation or variational approach for the
resolution of well posed problems is to replace the equation by an
equivalent formulation which can be solved by Hilbert space methods
(in the linear case) or by Minty-Browder methods (in the nonlinear case).
In this talk, we recall the variational approach of Gregoire Allaire in
the classical case for stationary and evolution problems.
We prove variational formulations for nonlocal problems (Riesz
potentials) and for quasilinear elliptic problems.
We then present a numerical analysis for the weighted p-Laplacian.
-
Alexander Mielke (WIAS Berlin): Gradient structures and uniform global decay
for reaction-diffusion systems
2013/04/25, 17:15, V2-210/216,
-
Andre Schenke: Exponentielle Dichotomien für nichtinvertierbare
Systeme
2013/04/19, 14:15, V5-148, AG Dynamische Systeme
Abstract: Dieser Vortrag behandelt die Verallgemeinerung des
Dichotomiebegriffes für nichtinvertierbare dynamische Systeme. Die
Definition wird motiviert und es werden elementare Eigenschaften und
Beispiele behandelt sowie Unterschiede zum "gewöhnlichen"
Dichotomiebegriff für invertierbare Systeme aufgezeigt. Die Projektoren
etwa sind im Falle J=Z nicht eindeutig und die Charakterisierung von
Bild und Kern der Projektoren mittels Quasibeschränktheit gelingt nur
unvollständig.
Eine Lösung dieses Problems bietet der Begriff der Regularität,
der im zweiten Teil des Vortrags besprochen wird.
-
Abderrahman Boukricha (Tunis)
Koautoren: Imed Ghanmi, Rochdi Jebari: Numerical Approximation of solutions of
Nonlinear Partial Differential Equations by Homotopy Perturbation
Method (HPM) and Adomian Decomposition Method (ADM)
2013/04/12, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this work, the homotopy perturbation method (HPM) and the
Adomian decomposition method (ADM) are presented.
These methods provide numerical approximations for solutions of
non-linear partial differential equations. The solutions of these
non-linear problems are approached by series with easily computable
partial sums (using Maple for HPM and Mathematica for ADM).
The numerical approximation in cases, where the exact solutions
(resp. other approximations) are known, turns out to be very good
(resp. yields better approximations). Ther results show that HPM and
ADM are very effective and simple.
-
Dietrich Neumann (Bielefeld) : Diskrete Approximation nichtlinearer
Eigenwertprobleme mit Multiplizitäten
2013/01/28, 16:15, V5-148, AG Dynamische Systeme
-
Wolf-Jürgen Beyn (Bielefeld) : Continuation and Collapse of Homoclinic Tangles
2013/01/25, 14:15, V5-148, Seminar Numerical Analysis
Abstract: By a classical theorem (Birkhoff, Smale, Shilnikov),transversal
homoclinic points of maps lead to shift dynamics on a maximal invariant set,
also referred to as a homoclinic tangle. In our work we analyze the fate of
homoclinic tangles in parameterized systems from the viewpoint of numerical
continuation and bifurcation theory. The main bifurcation result shows that
the maximal invariant set near a homoclinic tangency, where two homoclinic
tangles collide, can be characterized by a set of bifurcation equations that
is indexed by a symbolic sequence.
For the Henon family we investigate in detail the bifurcation structure of
multi-humped homoclinic orbits originating from several tangencies. The
emerging homoclinic network is explained by combining our bifurcation
result with graph-theoretical arguments.
This is joint work with Thorsten Hüls.
-
Sebastian Schmitz (Lugano): Optimal Realiability in Design for Fatigue Life
2013/01/22, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Fatigue describes the damage or failure of material under cyclic loading.
Activation and deactivation
operations of technical units are important examples in engineering where
fatigue and especially low-cycle fatigue (LCF) play an essential role. A
significant scatter in fatigue life for many materials results in the
necessity of advanced probabilistic models for fatigue. Moreover,
structural shape optimization is of increasing interest in engineering,
where with respect to fatigue the cost functionals are motivated by their
predictability for the integrity of the component after a certain number
of load cycles. But mathematical properties such as the existence of the
shape derivatives are desirable, too. Deterministic design philosophies
that derive a predicted component life from the average life of the most
loaded point on the component plus a safety factor accounting for the
scatter band do not have this favorable property, as taking maxima is not
a differentiable operation. Here, we present a new local probabilistic
model for LCF. This model constitutes a new link between reliability
statistics, shape optimization and structural analysis
which considers the perspective of fatigue but also fits into the
mathematical setting of shape optimization. The cost functionals derived in
this way are too singular to be \(H^1\) lower semi-continuous. We therefore
have to modify the existence proof of optimal shapes for the case of
sufficiently smooth shapes using elliptic regularity, uniform Schauder
estimates and compactness of certain subsets in
\(C^k(\Omega^\textrm{ext},\mathbb{R})\) via the Arcela-Ascoli theorem, where
\(\Omega^\textrm{ext}\) is some shape containing all
admissible shapes. Moreover, we extend our existence results to high-cycle
fatigue (HCF) and deterministic models of fatigue.
-
Lennart Esdar (Bielefeld): Existenz und Stabilität wandernder Wellen
für eine nichtlineare Wellengleichung
2013/01/08, 16:15, V5-148, Seminar Numerical Analysis
-
Jochen Röndigs (Bielefeld): Reaction Diffusion Systems on Infinite Lattices
2012/11/30, 14:15, V5-148, AG Dynamische Systeme
Abstract: This talk is about the evolution of reaction diffusion
systems on an infinite dimensional space and their finite
dimensional approximations.
The main result is the upper semicontinuity of an approximate attractor
on a finite lattice with respect to the attractor of the original
system on the infinite lattice. We take a short look at
characteristic properties of the equations and then derive a priori estimates
which establish the existence of a global attractor, both on the finite
and the infinite lattice.
-
Rudolf Dürksen: Unterhalbstetigkeit von Attraktoren
2012/11/20, 16:15, V5-148, AG Dynamische Systeme
Abstract:
Wir betrachten eine autonome Differentialgleichung der Form
\(\frac{du}{dt}=f(u)\), \(u(0)=U\in\mathbb R^p\), die mit einem
Einschrittverfahren \(U_{n+1}=S_{\Delta t}^1U_n\), \(U_0=U\) gelöst
wird. Für den diskretisierten Attraktor \(\mathcal{A}_{\Delta t}\)
haben wir gesehen, dass die Oberhalbstetigkeit
\(\text{dist}\left(\mathcal{A}_{\Delta t},\mathcal{A}\right)\rightarrow 0\)
gegeben ist.
Wir werden zeigen, dass unter zusätzlichen Voraussetzungen auch die
Unterhalbstetigkeit \(\text{dist}\left(\mathcal{A},\mathcal{A}_{\Delta
t}\right)\rightarrow 0\) gegeben ist, sodass insgesamt
\(\text{dist}_H\left(\mathcal{A},\mathcal{A}_{\Delta t}\right)\rightarrow 0\)
für \(\Delta t \to 0\) gilt.
-
Andre Schenke: Hyperzyklische Operatoren und der Satz von Grivaux
2012/11/16, 14:15, V5-148, AG Dynamische Systeme
Abstract:
Der Satz von Grivaux gibt eine Charakterisierung derjenigen Mengen
eines separablen unendlich-dimensionalen Banachraumes an, die Orbits
eines hyperzyklischen Operators sind.
Behandelt werden die grundlegenden Ideen für die Formulierung des
Satzes von Grivaux, der Beweis im Banachraumfall sowie eine kurze
Beweisskizze für den Fall von Fréchet-Räumen mit einer stetigen Norm.
-
Alina Girod: Diskretisierung heterokliner Orbits
2012/10/16, 16:15, V5-148, AG Dynamische Systeme
Abstract: Erste Betrachtung ist ein kontinuierliches Dynamisches
System, wobei der Begriff nicht-entarteter Verbindungsorbit
eingeführt wird.
Diese und 1-tangentiale Orbits betrachten wir dann im diskretisierten Fall.
Zwischenziel ist es zu zeigen, dass diskretisierte Verbindungsorbits
des kontinuierlichen Systems 1-tangentiale nicht-entartete
heterokline Orbits des \( \varepsilon \)-Flusses sind.
Allgemeines Ziel ist es zu zeigen, dass eine Diskretisierung mit einem
Einschritt-Verfahren unter gewissen Annahmen mindestens zwei
1-tangentiale nicht-entartete heterokline Orbits besitzt.
-
Thorsten Hüls: Homoclinic trajectories of non-autonomous maps
2012/10/09, 16:15, V5-148, Seminar Numerical Analysis
Abstract: For time-dependent dynamical systems of the form
\(x_{n+1} = f_n(x_n), n \in \mathbb{Z}\)
homoclinic trajectories are the non-autonomous analog of
homoclinic orbits from the autonomous world.
More precisely, two trajectories \((x_n)_{n\in\mathbb{Z}}\),
\((y_n)_{n\in\mathbb{Z}}\) are called homoclinic to each other, if
\(\lim_{n\to \pm \infty} \|x_n - y_n\| = 0\).
Two boundary value problems are introduced, the solution of which yield
finite approximations of these trajectories. Under certain hyperbolicity
assumptions, we prove existence, uniqueness and
error estimates.
Extending these ideas, we also propose adequate notions for heteroclinic
orbits in non-autonomous
systems.
The resulting algorithms and error estimates are
illustrated by an example.
-
Stefanie Hittmeyer (Auckland): Interacting global manifolds in a planar map
model of wild chaos
2012/07/20, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We study a non-invertible planar map that has been suggested by
Bamon, Kiwi and Rivera-Letelier as a model for a new type of chaotic
dynamics in continuous-time dynamical systems of dimension at least five;
one also speaks of wild Lorenz-like chaos. This map opens up the origin (the
critical point) to an open disk and wraps the plane twice around it; inside
this disk there are no preimages. The bounding critical circle and its
images, together with the critical point and its preimages form the
so-called critical set. This set interacts with a saddle fixed point and its
stable and unstable sets.
Advanced numerical techniques enable us to study how the stable and unstable
sets change as a parameter is varied along a path towards the wild chaotic
regime. We find sequences of bifurcations, which are of two types. First,
there are bifurcations that also occur in invertible maps, such as
homoclinic tangencies. Second, we find bifurcations specific to
non-invertible maps: interactions of the stable and unstable sets with the
critical set, which also cause changes (such as self-intersections) of the
topology of these global invariant sets. Overall, a consistent sequence of
both types of bifurcations emerges, which we present as a first attempt
towards explaining the geometric nature of wild chaos.
-
Martin Arnold: Ein Lie-Gruppen-DAE-Integrator
2012/07/09, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Lage und Orientierung des Starrkörpers lassen sich ohne
Singularitäten als Elemente geeigneter Lie-Gruppen beschreiben. Schon 1989
haben Géradin und Cardona diese Darstellung zu einer Finite-
Elemente-Beschreibung flexibler Mehrkörpersysteme verallgemeinert.
Bezieht man die für mechanische Mehrkörpersysteme typischen
(holonomen) Zwangsbedingungen ein, so ergeben sich
differentiell-algebraische Systeme
(engl.: differential-algebraic equations, DAEs) vom Index 3 auf
einer (Matrix-)Lie-Gruppe.
Bei der direkten Zeitintegration dieses Index-3-Systems mit dem aus
der Strukturdynamik bekannten Generalized-/(alpha/)-Verfahren) beobachtet man -
ebenso wie bei Anwendung
dieses Verfahrens in linearen Räumen - eine Ordnungsreduktion zu
Beginn der Integration. Eine detaillierte, auf die
zugrunde liegende Lie-Gruppen-Struktur zugeschnittene
Konvergenzanalyse zeigt, wie die Ordnungsreduktion durch modifizierte
Startwertedes Zeitintegrationsverfahrens vermieden werden
kann. Die Ergebnisse der theoretischen Untersuchungen werden durch
numerische Tests für einfache
Benchmarkprobleme verifiziert.
-
Andrea Walther (Paderborn): On an Inexact Trust-region Approach for
Inequality Constrained Optimization
2012/06/29, 12:45, V5-148, Seminar Numerical Analysis
Abstract: This talk presents a trust-region SQP
algorithm for the solution of minimization problems with
nonlinear inequality constraints. The approach works only with an
approximation of the constraint Jacobian. Hence, it is well
suited for optimization problems of moderate size but with dense
constraint Jacobian. The accuracy requirements for the presented
first-order global convergence result can be verified easily
during the optimization process. Numerical results for some test
problems are shown.
-
Sonja Cox (Universität Innsbruck) : Pathwise estimates for the implicit Euler
scheme for SDEs in Banach spaces
2012/06/08, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In the first part of my talk I will explain what is meant by
pathwise estimates for an approximation scheme of a stochastic
differential equation (SDE), and why such estimates are of importance.
In recent work by Jan van Neerven and myself, we obtained pathwise
estimates for the implicit Euler scheme for SDEs in Banach spaces. In
the second half of the talk I will sketch how we obtained these results
and indicate what challenges arise when working in Banach spaces.
-
Wilhelm Stannat (TU Berlin, Bernstein Netzwerk) : Stochastic stability of travelling waves in the
Nagumo equation
2012/06/01, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
-
Michael Scheutzow (TU Berlin) (Projekte A3, B3, B4) : Uniqueness of invariant measures via asymptotic
coupling with applications to stochastic delay equations
2012/05/25, 14:00!!, V5-148,
Abstract:
We provide sufficient conditions for the uniqueness of an
invariant measure for a Markov process in terms of the existence of a
generalized asymptotic coupling.
This method is particularly useful in cases in which the transition
probabilities for different initial conditions are mutually singular
(and hence classical methods for proving uniqueness fail).
We apply the result to stochastic delay equations.
This is joint work with Martin Hairer and Jonathan Mattingly.
-
Heiko Prange : Hinreichende Bedingungen für LR-Chaos in
zeitdiskreten dynamischen Systemen
2012/05/21, 16:15, V5-148, AG Dynamische Systeme
Abstract:
Ähnlich wie die chaotische Dynamik des Shift-Operators auf der Menge
der Symbole 0 und 1 lässt sich der Begriff des Links-Rechts Chaos auf
Teilmengen L und R eines zeitdiskreten dynamischen Systems
definieren. Die Kern-Idee zum Aufspüren von LR-Chaos
in zeitdiskreten dynamischen Systemen ist es, periodische
Punkte zu vorgegebenen Links-Rechts Sequenzen zu finden.
Diese periodischen Punkte kann man als Fixpunkte von iterierten
Funktionen betrachten. So führt der Miranda-Fixpunktsatz zu Gebieten
mit LR-chaotischer Dynamik.
-
Christian Pötzsche (Klagenfurt) : Feinstruktur des Dichotomie-Spektrum
2012/05/18, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Das Dichotomie-Spektrum (auch dynamisches oder Sacker-Sell Spektrum)
ist ein wesentlicher Begriff innerhalb der Theorie nichtautonomer
dynamischer Systeme, da es zentrale Information zur Stabilität,
Hyperbolizität und Robustheit von Lösungen enthält.
Aktuelle Anwendungen in der Verzweigungstheorie erfordern jedoch eine
detailliertere Einsicht in dessen Feinstruktur. Auf dieser Basis
untersuchen wir eine hilfreiche Verbindung zwischen
Dichotomie-Spektrum und Operator-Theorie, welche das Langzeitverhalten
nichtautonomer Gleichungen mit dem Punkt-, Surjektivitäts- oder
Fredholm-Spektrum gewichteter Shift-Operatoren in Beziehung
setzt. Dieser Zusammenhang führt auf entsprechende Teilmengen des
Dichotomie-Spektrums, welche nicht nur Verzweigungen bereits auf
linearer Ebene klassifizieren, sondern auch Beweise über das
asymptotische Verhalten von Differential- und Differenzengleichungen
vereinfacht.
-
Rudolf Dürksen (Bielefeld) : Oberhalbstetigkeit von Attraktoren
2012/05/07, 16:15, V5-148, AG Dynamische Systeme
Abstract:
Sei eine autonome Differentialgleichung der Form \(\frac{du}{dt}=f(u),
u(0)=U\in\mathbb R^p\), gegeben. Bekanntlich kann diese
Differentialgleichung mit einem Einschrittverfahren \(U_{n+1}=S_{\Delta
t}^1U_n, U_0=U\) gelöst werden. Wir werden das Verhalten des
diskretisierten Attraktors \(\mathcal{A}_{\Delta t}\) untersuchen und
dabei feststellen, dass in unserem Fall die Oberhalbstetigkeit gegeben
ist, d. h. dass \(dist\left(\mathcal{A}_{\Delta
t},\mathcal{A}\right)\rightarrow 0\) gilt.
-
Jan Giesselmann (Stuttgart) : Some ideas for the numerical discrtization of the
Navier-Stokes-Korteweg model
2012/04/30, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
-
Sergey Tikhomirov : Shadowing lemma for partially hyperbolic systems
2012/01/30, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We say that diffeomorphism \(f\) of a manifold \(M\) is partially
hyperbolic if tangent bundle of \(M\)
admits an invariant splitting \(E^s + E^c + E^u\),
such that \(E^s\) and \(E^u\) are uniformly hyperbolic and \(E^c\) is not.
If \(E^c \) is empty diffeomorphism is uniformly hyperbolic.
Shadowing lemma says that in hyperbolic systems any pseudotrajectory
can be shadowed by an exact trajectory.
We introduce notion of central pseudotrajectory
and prove that in partially hyperbolic systems any pseudotrajectory
can be shadowed by a central pseudotrajectory.
-
Annika Lang (ETH Zürich): Simulation of stochastic processes
2012/01/23, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Hilbert-space-valued stochastic processes such as Q-Wiener
processes are in general the driving noise of stochastic partial differential
equations (SPDEs for short). To approximate the solution of an SPDE, it
is in general necessary to approximate the driving noise. In this talk,
different approximation methods for stochastic processes and the
corresponding Ito integrals are introduced and their simulations are
presented. As an application to the approximation of solutions of SPDEs
it is shown how to equilibrate the discretization errors of the space
and time approximation of the SPDE and the error of the driving noise
approximation.
-
Lennart Esdar : Solitärwellen in Hamiltonschen Systemen
2012/01/20, 14:15, V5-148, AG Dynamische Systeme
Abstract:
-
Christian Lubich (Tübingen): Modulated Fourier expansions for highly
oscillatory problems
2011/12/09, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Modulated Fourier expansions are an analytic technique for
understanding the behaviour of weakly nonlinear oscillatory problems
over very long times. The technique applies to highly oscillatory
ODEs, to particle systems such as the Fermi-Pasta-Ulam lattice, to
Hamiltonian PDEs such as nonlinear Schrödinger and wave equations,
as well as to their numerical discretizations. The approach first came
up about a decade ago in the numerical analysis of highly oscillatory
ODEs, where it explained remarkable long-time energy conservation
properties of numerical integrators, and has since been used to
analyse long-time properties of various types of problems as mentioned
above, both for the continuous equations and their numerical
discretizations. In addition to their role as an analytical tool
originating from numerics, modulated Fourier expansions have also been
found useful as a numerical approximation method for highly
oscillatory problems. Most of the talk is based on joint work with
Ernst Hairer, some parts also with David Cohen, Ludwig Gauckler and
Daniel Weiss.
-
Matthias Ehrhardt : Absorbing Boundary Conditions for Hyperbolic Systems
2011/12/05, 16:15, V5-148, Seminar Numerical Analysis
Abstract: This talk deals with absorbing boundary conditions (ABCs)
for hyperbolic systems in one and two space dimensions. We prove the strict
well-posedness of the resulting initial boundary value problem in 1D.
Afterwards we establish the GKS-stability of the corresponding
Lax-Wendroff-type finite difference scheme. Hereby, we have to extend
the classical proofs, since the (discretized) ABCs do not t the standard
form of boundary conditions for hyperbolic systems.
In the second part we present the approach of deriving so-called
discrete absorbing boundary conditions, i.e. ABCs constructed on a
purely discrete level. These discrete ABCs are better adapted to the
interior scheme: they lead to less unphysical reflections and the
resulting overall scheme has better stability properties.
Finally, we sketch briefly how ABCs can be derived for nonlinear
hyperbolic systems.
-
Thorsten Rieß (Universität Konstanz): N-heteroclinic orbits near non-reversible
homoclinic snaking
2011/11/28, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Non-reversible homoclinic snaking of a codimension-1
homoclinic orbit to an equilibrium is a phenomenon that is known to
occur near certain heteroclinic equilibrium-to-periodic (EtoP) cycles.
We show numerically that there exist other connecting orbits in the
neighbourhood of the homoclinic snaking for a specific family of
three-dimensional vector fields. In particular, we use a numerical
method based on Lin's method to compute codimension-1 PtoE connecting
orbits that take additional excursions along the EtoP cycle before
connecting up, so-called N-heteroclinic PtoE orbits. It turns out that
the N-heteroclinic PtoE orbits exist on isolas in parameter space.
-
Sergei Pilyugin (St. Petersburg): Lipschitz shadowing and structural stability:
the case of flows
2011/10/11, 16:30, V5-148, Seminar Numerical Analysis
Abstract: Recently, it was shown that for diffeomorphisms, Lipschitz
shadowing is equivalent to structural stability (S.Yu. Pilyugin
and S.B. Tikhomirov, Nonlinearity, vol. 23, 2509-2515, 2010).
In this talk, we discuss a similar result for flows and explain
the appearing difficulties (the main difficulty is created by the
absence of Mane's theorem characterizing structural stability
in terms of strong transversality).
This is a joint research with K.Palmer and S.Tikhomirov.
-
Richard Norton (Oxford): Finite Element Approximation of an H1 Gradient Flow
2011/07/11, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
I consider the discretization error in space and time of an H1
gradient flow for an energy integral where the energy density is given
by the sum of a double-well potential term and a bending energy
term. This problem is equivalent to a nonlinear heat equation with
nonlocal nonlinearity. The approach for the error analysis is to adapt
standard error analysis theory developed for nonlinear heat equations to
bound the discretization error in terms of the mesh size and time step
as well as energy parameters. In particular, I carefully track how the
size of the bending energy affects the error bounds.
-
Piotr Gwiazda: On scalar hyperbolic conservation laws with a
discontinuous flux
2011/07/04, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We study the Cauchy problem for scalar hyperbolic conservation
laws with fluxes that can have jump
discontinuities with respect to the unknown and only measurable with
respect to the space variable. We introduce a new concept of entropy
weak and measure-valued solution that is consistent with the
standard one for continuous fluxes. We then answer the question as to what
kind of properties the fluxes should posses in order to establish the
existence and/or uniqueness of various notions of solutions. In
any space dimension we establish the existence of measure-valued entropy
solution for fluxes having jump discontinuities, under additional
assumptions we prove existence of weak solutions.
-
Ewelina Zatorska: On a new approach applied to the
time--discretization of the compressible Navier--Stokes equations
2011/06/20, 16:15, V5-148, Seminar Numerical Analysis
-
Matthias Groncki: Markovketten und der Metropolis-Algorithmus
2011/06/10, 14:15, V5-148, AG Dynamische Systeme
-
Gert Lube (Göttingen): A Projection-based Variational Multiscale Method
for Turbulent Incompressible Flows
2011/06/06, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
We consider the Navier-Stokes Fourier model for time-dependent,
non-isothermal, incompressible flows. This nonlinear evolution problem
has a generalized solution. Moreover, in case of a
regularization with the well-known Smagorinsky turbulence model, it is
uniquely solvable. Unfortunately,
the latter model is too diffusive in application to turbulent
flows. As a remedy, a variational
multiscale (VMS) method for the large-eddy simulation is considered.
Following a general proposal in [1], our VMS-approach relies on local
projection of the velocity
deformation tensor and the temperature gradient together with a
grad-div stabilization of the
divergence-free constraint. Semi-discrete stability and a priori error
estimates are derived in the
case of inf-sup stable approximation of velocity and pressure, see [2,
3]. In particular, rather general
nonlinear and piecewise constant coefficients of the subgrid models
for the unresolved scales
of velocity and pressure are allowed, including the classical
Smagorinsky model. We give a critical
discussion of the results in view of the employed Gronwall
argument. Moreover, we discuss aspects
of the time discretization and of its analysis.
Finally, we present and discuss numerical simulations for basic
benchmark problems like decaying
homogeneous isotropic turbulence, channel flow and natural convection
in a differentially heatedcavity.
References
[1] W. Layton, A connection between subgrid scale eddy viscosity and
mixed methods. Appl. Math. Comput. 133 (2002), 147-157.
[2] L. Röhe, and G. Lube, Analysis of a variational multiscale method
for Large-Eddy simulation and
its application to homogeneous isotropic turbulence,
Comput. Meths. Appl. Mech. Engrg. 199 (2010), 2331-2342.
[3] J. Löwe, and G. Lube, A projection-based variational multiscale
method for Large Eddy simulation
with application to non-isothermal free convection problems, NAM
Preprint, Georg-August-Universität zu Göttingen, 2010. Accepted for
Math. Model. Meths. Appl. Sc. (5/2011).
-
Denny Otten (Bielefeld): Exponential decay of two-dimensional rotating waves
2011/06/03, 14:15, V5-148, AG Dynamische Systeme
-
Marcin Malogrosz: A Model of Morphogen Transport Well-Posedness
and Asymptotical Behaviour
2011/05/30, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Morphogen transport (MT) is a process occurring in the tissue of life
organisms, affecting cell differentiation. There is a vast literature concerning
modeling of MT but as for now there is still no consensus on what is the
exact mechanism of the movement of morphogen particles. Various types
of diffusion, bucket brigade, reactions with other particles are among those
being considered.
I will present my recent results concerning well-posedness and asymp-
totical behavior of the solutions of the model proposed in [1] (semilinear
parabolic PDE coupled with ODE), where MT is being modeled by passive
diffusion and binding-unbinding reactions with receptors.
My results are nontrivial extension of those obtained in [2], where the
same model is being considered in 1D setting. Using theory of analytic
semigroups I improve dimension of the domain (from 1 to arbitrary) and
topology of the convergence of solution to unique equilibrium (from \(L_2
\times L_2\) to \(C^{1,\alpha} \times C^{0,\alpha}\)).
References
[1] Lander, A. D., Nie, Q., Wan, Y. M. Do Morphogen Gradients Arise by
Diffusion? Dev. Cell, Vol. 2, pp. 785-796.
[2] Krzyzanowski, P., Laurençcot, P., Wrzosek, D. Well-posedness and con-
vergence to the steady state for a model of morphogen transport, SIAM
J.MATH. ANAL. Vol. 40, No. 5, pp. 1725-1749.
-
Raphael Kruse (Bielefeld): FEniCS: Finite Elements in Computer Science
eine Software zur Loesung elliptischer und parabolischer Aufgaben
2011/05/13, 14:15, V5-148, AG Dynamische Systeme
-
Maria Lopez Fernandez (Uni Zürich): Contour integral methods for parabolic equations
2011/05/09, 16:15, V5-148, Seminar Numerical Analysis
-
Andrzej Warzynski: 30 Years of Residual Distribution Schemes for
Hyperbolic Conservation Laws
2011/05/02, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The most popular schemes for hyperbolic conservation laws
are based on
1-dimensional concepts (i. e. Riemann solver) which are then heuristically
extended and applied to flow problems in more than 1 space dimension.
Recently, intensive research has been being carried out focused on the
development of `multidimensional upwind' schemes. This new class of
numerical algorithms is far better able to incorporate genuinely
multidimensional phenomena described by conservation laws and thus to
predict the fluid flow more accurately.
In this talk I shall first briefly justify the need for genuinely
multidimensional approach and then describe a particular class of
multidimensional upwind schemes, namely those developed within the
Residual Distribution (RD) framework. This will include design principles
for the steady state RD schetime-dependent problems.
Finally, I shall focus on the recently proposed explicit Runge-Kutta RD
[1] and discontinuous RD schemes [2], and discuss the possibility of
combining these two approaches. This is an ongoing research conducted in
collaboration with M. E. Hubbard and M. Ricchiutto.
[1] R. Abgrall, M. Ricchiuto 'Explicit Runge-Kutta residual distribution
schemes for time dependent problems: second order case.' J. Comput.
Phys. 229(16), 5653--5691, 2010.
[2] M. E. Hubbard 'Discontinuous fluctuation distribution.'
J. Comput. Phys. 227(24), 10125--10147, 2008.
-
Janning Barembruch (Bielefeld): Diskretisierung der Hopf-Bifurkation
2011/04/15, 14:15, V5-148, AG Dynamische Systeme
-
Guy Vallet (Pau): On some Barenblatt's problems
2011/04/11, 16:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we will be interested in the problem of
Barenblatt's type:
\(f(\partial_{t}u)-\Delta_pu - \epsilon \Delta \partial_{t}u =g\quad
\textrm { in }\ Q.\)
In a first part, we will consider the hilbertian case \(p=2\), then
when \(p> \frac{2d}{d+2}\) and when \(p\) is a function of \(x\).
We finish with some numerical simulations of the hilbertian case.
-
Janning Barembruch (Bielefeld): Diskretisierung der Hopf-Bifurkation
2011/04/08, 14:15, V5-148, AG Dynamische Systeme
-
Raphael Kruse : Finite-Elemente Methoden für PDEs
2011/02/04, 14:15, V5-148, AG Dynamische Systeme
-
Heiko Berninger (FU Berlin): On Domain Decomposition Methods for Nonlinear
Transmission Problems
2011/01/31, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Consider a nonoverlapping decomposition of a domain \(\Omega\)
into subdomains \(\Omega_1\) and \(\Omega_2\). It is well known that instead
of solving \(-\triangle u = f\) on \(\Omega\), one can solve this equation on
\(\Omega_1\) and on \(\Omega_2\) if one additionally obeys the transmission
conditions \(u_1|_\Gamma = u_2|_\Gamma\) and \(\frac{\partial u_1}{\partial n}
= \frac{\partial u_2}{\partial n}\) across the interface \(\Gamma = \Omega_1
\cap \Omega_2\).
Furthermore, domain decomposition methods like the Dirichlet-Neumann or
the Robin method can be used to solve the transmission problem.
But what if the continuity condition \(u1|_\Gamma = u2|_\Gamma\) is replaced
by the more general one \(F_1(u_1|_\Gamma) = F_2(u_2|_\Gamma)\) with - possibly
nonlinear - operators \(F_1, F_2\) acting on the trace space \(H^{\frac{1}{2}}_{00}
(\Gamma)\)? We discuss variations of this situation, sketch proofs for
well-posedness and convergence of corresponding nonlinear domain decomposition
methods, and address open questions as well as limitations inherent in the
proofs.
These situations occur in nature when we intend to simulate saturated -
unsaturated groundwater flow in a way that we find quite nice. This is
because we have a solver-friendly discretization for the Richards equation
in homogeneous soil and monotone multigrid as a powerful solver in this
case. We present numerical examples which also address optimization of the
domain decomposition methods.
Joint work with:
R. Kornhuber, O. Sander (FU Berlin), M. Discacciati (EPFL Lausanne)
-
Raphael Kruse : Finite-Elemente Methoden für PDEs
2011/01/28, 14:15, V5-148, AG Dynamische Systeme
-
José Augusto Ferreira (Coimbra):
2011/01/24, 17:15, V5-148, Seminar Numerical Analysis
Abstract: Integro-differential equations of Volterra type
arise, naturally, in many applications such as for instance heat
conduction in materials with memory, diffusion in polymers and
diffusion in porous media. The aim of this talk is to presente
supraconvergent finite difference methods for such
integro-differential equations. As these finite difference methods
can be seen as piecewise linear finite elements method combined with
special quadrature formulas, our results are superconvergence results
in the finite element language.
-
Bernd Simeon (Kaiserslautern): Transiente Sattelpunktprobleme und Anwendungen in der Mechanik
2011/01/24, 16:15, V5-148, Seminar Numerical Analysis
Abstract: n. a.
-
Jens Rottmann-Matthes : Optimale Integralabschätzungen für
die Laplacetransformation
2011/01/21, 14:15, V5-148, AG Dynamische Systeme
-
Yi Zhou : Die Takens-Bogdanov Singularitaet
2011/01/14, 14:15, V5-148, AG Dynamische Systeme
-
Sven Kreimer-Huenke : Spektralmethoden fuer Evolutionsgleichungen
2010/12/17, 14:15, V5-148, AG Dynamische Systeme
-
Filip Rindler (Oxford): Rigidity for some differential inclusions
involving the gradient and the symmetrized gradient
2010/12/14, 18:00, V5-148, Seminar Evolutionsgleichungen
Abstract: We look at (smooth) functions
\(u:\mathbb{R}^2\to\mathbb{R}^2\) whose gradient
can be written in the form \(\nabla u(x)=P g(x)\)
for a fixed \(\mathbb{R}^{2\times 2}\)-matrix \(P\)
and a smooth scalar function \(g:\mathbb{R}^2\to \mathbb{R}\).
Similarly, replacing the gradient by the symmetrized gradient, we
consider (smooth) solutions \(u:\mathbb{R}^2\to\mathbb{R}^2\) of
\(\left( \nabla u(x)+ (\nabla u(x))^T\right)/2 = Pg(x),\)
with \(P\) a fixed symmetric \(\mathbb{R}^{2\times 2}\)-matrix
and \(g\) as before.
I will establish conditions on the existence of such solutions,
depending on the value of \(P\), and I will prove some (probably
unexpected) 'rigidity' properties of any function \(u\) satisfying
one of the above properties. The situation in two dimensions
already contains all
the essential features and exposes fascinating connections to
Harmonic Function Theory and Complex Analysis.
Whereas the presented results are new (particularly in the case
of the symme trized gradient) and are a core ingredient in the
results described in my se minar talk, the discussion is
completely elementary and involves only first-year
multi-dimensional Differential Calculus. I will also point out a
few references for further study of such 'rigidity arguments'.
-
Filip Rindler (Oxford): Minimization problems in the space BD of
functions of bounded deformation
2010/12/13, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The space BD of functions of bounded deformation consists of all
L^1-functions whose distributional symmetrized derivative
(defined by duality with the symmetrized gradient (Δ u + Δ
u^T)/2) is representable as a finite Radon measure.
Such functions play an essential role in modern theories of
(linear) elasto-plasticity in a variational framework. In this talk, I will
present the first general theorem on solvability of minimization
problems for integral functionals with linear growth on the whole
space BD.
The main novelty is that we allow for non-vanishing Cantor-parts in
the symmetrized derivative, corresponding to fractal phenomena in
nature.
The proof is accomplished via Jensen-type inequalities for generalized
Young measures and a construction of good blow-ups, which is based on
local rigidity arguments for some
differential inclusions involving symmetrized gradients. This strategy
allows us to prove the crucial lower semicontinuity result
without an Alberti-type theorem in BD, which is not available at
present. A similar strategy also allows to considerably simplify the proof of
the classical lower semicontinuity theorem in the space BV of functions of
bounded variation.
-
Eduard Feireisl (Prag): Asymptotic behavior of compressible viscous
fluids
2010/12/09, 17:15, V3-201, Mathematical Colloquium
Abstract: We discuss the long-time behavior of solutions to
energetically closed fluid systems. By this we mean that the system possesses
an energy functional, the value of which is conserved in time, and an entropy,
the total amount of which is nondecreasing.
Various topics are addressed: Equilibrium solutions, thermodynamic stability,
the existence of attractors, boundedness of globaltrajectories
-
Eduard Feireisl (Prag): Singular limits of compressible fluids
driven by large external forces
2010/12/07, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We consider a compressible fluid excited by large
external forces. Using the abstract result of Kato we show
that the acoustic component of the velocity vanishes in the
incompressible regime although there is a strong interaction between
the force and acoustic waves. Applications are given to rotating
fluid systems.
-
Lina Fruendt : Symbolische Dynamik und transversale homokline Punkte
2010/12/03, 14:15, V5-148, AG Dynamische Systeme
-
Martin Stynes (Cork): A new finite element method for singularly
perturbed reaction-diffusion problems
2010/11/30, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Consider the singularly perturbed linear
reaction-diffusion problem -ε^2 Δ u + bu = f in
Ω ⊂ R^d, u=0 on δΩ, where
0 < ε << 1, b > 0 and d≥ 2. It is argued that for this type
of problem, the standard energy
norm is too weak a norm to meas ure adequately the errors in solutions
computed by finite element methods. A stronger norm is introduced and a
mixed finite element constructed whose solution is quasi-optimal in this
new norm, and a duality argument is used to show that this solution
attains a higher order of convergence in the L^2 norm. Error bounds
derived from these analyses are presented for the cases d=2,3. For a
problem posed on the unit square in R^2, an error
bound that is uniform in ε is derived when the new method is
implemented on a Shishkin mesh. Numerical results are presented to show
the superiority of the new method over current finite element methods
for singularly perturbed reaction-diffusion problems.
-
Lina Fruendt : Symbolische Dynamik und transversale homokline Punkte
2010/11/26, 14:15, V5-148, AG Dynamische Systeme
-
Aneta Wróblewska: Generalized Stokes system in Orlicz spaces
2010/11/22, 16:15, V5-148, Seminar Numerical Analysis
Abstract: The talk concerns the generalized Stokes system
∂_t u - div S(t, x,Du) + ∇ p = f in (0, T) × Ω
div u = 0 in (0, T) × Ω
u(0, x) = u_0 in Ω
u(t, x) = 0 on (0, T) ×
∂ Ω,
with the nonlinear viscous term having growth conditions prescribed
by an N-function.
We will consider the case of monotone functions. Our main interest is
directed to relaxing
the assumptions on the N-function. To prove existence of weak
solutions to our equations we will show the Korn-Sobolev inequality
for anisotropic Orlicz spaces and the fact that
closures of smooth compactly supported functions w.r.t. modular and
weak star topology of symmetric gradient coincides.
-
Jens Rottmann-Matthes : Laplace-Transformation und Stabilitaet der
konvektiven Waermeleitungsgleichung
2010/11/19, 14:15, V5-148, AG Dynamische Systeme
-
François Murat (Paris) : How to solve second order elliptic equations
with right-hand side in L^1
2010/11/18, 17:15, V3-201, Mathematical Colloquium
Abstract:
In this lecture, I will consider the problem: find u such that
-div(A(x)Du) = f in Ω,
u = 0 on Ω
when the matrix A is coercive with measurable bounded coefficients and
when f belongs to L^1(Ω).
The main difficulty of the problem is to define a convenient notion of
solution.
Such a definition (the 'solution by transposition') was introduced by G.
Stampacchia in 1973.
However, this definition is essentially restricted to the linear case. In this
lecture, I will present the notion of 'renormalized solution', which can
be extended in a natural way to the case of a second order monotone
operator in divergence form posed on W^{1,p}_0 (Ω)
Definition: u is a renormalized solution of the problem if u : Ω
→ ℝ is measurable and a.e. finite
T_n(u) ∈ H^1_0 (Ω) for every n > 0,
1/n ∫ |DT_n(u)|^2 → 0 as n → + ∞,
-div(h(u)A(x)Du)+h'(u)A(x)DuDu = h(u)f in D'(Ω) for
every h ∈ C^1_c (ℝ)
This definition allows one to prove that the problem has a renormalized
solution, that this renormalized solution is unique, and that it depends
continuously on f, i.e. that in this framework the problem is well posed in
the sense of Hadamard.
-
Thomas Hanning : Numerische Berechnung invarianter Mannigfaltigkeiten
2010/11/05, 16:00, V5-148, AG Dynamische Systeme
-
Wolf-Juergen Beyn (Bielefeld) : Eine Integralmethode fuer nichtlineare
Eigenwertprobleme
2010/10/29, 14:15, V5-148, AG Dynamische Systeme
-
Petra Wittbold (Essen): On a nonlinear elliptic-parabolic
integro-differential equation with L^1-data
2010/10/27, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We consider an initial-boundary-value problem for a nonlinear
elliptic-parabolic integro-differential equation.
Equations of this type have been proposed to model flow through porous media
with memory effects and
nonlinear heat flow in certain dielectric materials at low temperatures.
Following classical results by Gripenberg, existence and uniqueness of a
generalized solution
to an associated abstract operator integro-differential equation can be
shown for abitrary L^1-data.
We study the question of regularity of this generalized solution and discuss
conditions that ensure
that the generalized solution is a strong, weak, entropy or renormalized
solution.
-
Thorsten Rohwedder (Berlin): The electronic Schrödinger equation and
an analysis for the continuous Coupled Cluster method
2010/10/25, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
Many properties of atoms, molecules and solid states are described
quite accurately
by solutions Ψ of the electronic Schrödinger equation H Ψ = E
Ψ , an
extremely high-dimensional operator eigenvalue equation for the Hamiltonian
H of the system under consideration. Of utmost interest is the smallest
eigenvalue of H and the corresponding eigenfunction, giving the ground state
energy and the electronic wave function describing the ground state,
respectively.
In the first part of this talk, the audience is introduced to the electronic
Schrödinger equation and the typical problems that arise when dealing with
this equation. We will then introduce the Coupled Cluster method, a method
that is standardly used in quantum chemistry for highly accurate calculations.
Coupled Cluster (CC) is standardly formulated as an ansatz for
the approximation of the Galerkin solution of the Schrödinger equation
with in a given discretisation [1].
We globalise this ansatz to infinite dimensional
spaces, thus obtaining an equivalent reformulation of the original, continuous
Schrödinger equation in terms of a root equation for a nonlinear
operator A, corresponding to the finite dimensional CC function f.
We show local strong
monontonicity of the CC function, derive some existence and uniqueness results
and prove a goal-oriented error estimator [2] for the ground state energy.
We conclude with a short discussion of the algorithmic treatment of the CC
root equation.
[1] R. Schneider, Num. Math. 113, 3, 2009.
[2] R. Becker, R. Rannacher, Acta Numerica 2000 (A. Iserlet, ed.), Cambridge
University Press, 2001
-
Etienne Emmrich (Bielefeld): Doubly nonlinear evolution equations of second order:
Existence and fully discrete approximation
2010/10/19, 18:00, V5-148, Seminar Evolutionsgleichungen
Abstract: The initial-value problem for doubly nonlinear evolution
equations of the type u'' + Au' + Bu = f is studied.
The time-dependent operator A is assumed to satisfy
a certain growth condition and is supposed to be the sum of
a monotone, coercive and hemicontinuous principal part and
a strongly continuous perturbation. The operator B is supposed to be the
sum of an operator that induces an inner product and a
non-monotone perturbation fulfilling a certain local Hölder-type
continuity condition.
Examples are viscous regularisations of equations arising in elasticity.
For a full discretisation combining a modification
of the Stürmer-Verlet method with an inner approximation
scheme, weak convergence of piecewise polynomial prolongations
of the discrete solutions are proven. These results also
imply the existence of a weak solution.
For the time discretisation, also variable time grids are allowed
as long as the deviation from equidistance is not too large.
A crucial step in the convergence proof is the equivalence with an
integro-differential equation of parabolic type.
In the case of non-monotone perturbations, a priori estimates
in fractional Sobolev-Slobodetskii spaces are a prerequisite
for the necessary compactness argument.
This is joint work with Mechthild Thalhammer (Innsbruck, Austria).
-
Boris Andreianov (Besançon): A one dimensional hyperbolic
particle-fluid interaction model, theory and numerical
approximation
2010/10/18, 16:15, V5-148, Seminar Numerical Analysis
Abstract: D'Alambert paradox states that, if the fluid viscosity
is neglected, the resulting force of the fluid action on
an immersed moving solid is zero. In other words, planes
could not fly if the air viscosity was totally neglected ...
In this talk we present a simple ''particle-in-Burgers''
model combining Burgers equation without viscosity and a viscous
interaction prenomenon between the fluid and a point particle.
The fluid equation becomes
u_t + ( (u^2)/2 )_x = -λ (u-h'(t)) δ_0(x-h(t))
where x=h(t) is the particle path, and δ_0 is the Dirac-δ.
The equation is coupled to an evolution equation
for the particle path h(⋅); the resulting force on the particle
is proportional to the jump of the normal fluxes of the fluid
across the particle path, and the whole model conserves the
quantity of movement.
We study well-posedness and numerical approximation
of the coupled problem by (as simple as possible)
finite volume schemes. Analysis tools have much in common
with the case of conservation laws with discontinuous flux.
Joint work with F. Lagoutiere, N. Seguin and T. Takahashi.
-
Rajesh Kumar (Magdeburg): Convergence analysis of a finite volume
scheme for solving non-linear aggregation-breakage equations
2010/09/20, 16:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk I will discuss the
stability and convergence analysis of a finite volume
scheme for solving aggregation-breakage equation which is a non-linear
integropartial differential equation.
First we rewrite this equation in conservative form and
then we apply the well known finite volume method. By showing
Lipschitz continuity of the numerical fluxes we found that
the scheme is second order convergent independently of the meshes for
pure breakage problem while for pure aggregation, due to non-linearity,
it shows second order convergent only on a uniform and non-uniform
smooth meshes. Furthermore, it gives first order convergence on a
non-uniform random grid. Finally, for the coupled problem as well, a
second order of convergence is shown on uniform and non-uniform smooth meshes
whereas first order convergence is obtained on random grid.
The mathematical results of convergence analysis are also validated numerically.
-
Hagen Eichel (Magdeburg): Supercloseness and Superconvergence of Stabilized Low Degree Finite Element Methods of The Stokes Problem
2010/09/20, 14:15, V5-148, Seminar Numerical Analysis
Abstract: The supercloseness and superconvergence property of stabilized finite element methods apllied to the Stokes problem are studied. We consider consistent residual based stabilization methods as well as inconsistent local projection type stabilizations. Moreover, we are able to show the supercloseness of the linear part of the MINI-element solution which has been previously observed in practical computations. The results on supercloseness hold on three-directional triangular, axiparallel rectangular, and bricktype meshes, respectively, but extensions to more general meshes are also discussed. Applying an appropriate postprocess to the computed solution, we establish superconvergence results. Numerical examples illustrate the theoretical predictions.
-
Eskil Hansen (Lund): Time stepping schemes for nonlinear
parabolic problems and a theorem by Brezis and Pazy
2010/08/16, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
There is a rich theory describing the approximation of nonlinear
semigroups. At its core one finds the results by Brezis and
Pazy, who generalize the classical linear results of Trotter and
Chernoff. Even though the theory was derived in the early
seventies, it is virtually unknown within the numerical
community. The aim of this talk is therefore to illustrate how
this nonlinear theory can be used as a corner stone when
deriving convergence for time stepping schemes applied to fully
nonlinear parabolic equations. In particular, we will illustrate
our framework by deriving the convergence for splitting schemes
and DIRK methods under minimal regularity
assumptions.
-
Mechthild Thalhammer (Innsbruck): Exponential operator splitting methods for nonlinear evolutionary problems involving critical parameters
2010/08/02, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
In this talk, the error behaviour of exponential operator
splitting methods for nonlinear evolutionary problems is
investigated. In particular, an exact local error
representation that is suitable in the presence of critical
parameters is deduced. Essential tools in the theoretical
analysis including time-dependent nonlinear Schrödinger
equations in the semi-classical regime as well as parabolic
initial-boundary value problems with high spatial gradients
are an abstract formulation of differential equations on
function spaces and the formal calculus of Lie-derivatives.
The general mechanism is exposed on the basis of the least
technical example method, the first-order Lie-Trotter
splitting. The conclusion that exponential operator
splitting methods are favourable for the time-integration of
nonlinear Schrödinger equations in the semi-classical
regime with Wentzel-Kramers-Brillouin initial condition under
the time stepsize restriction
h = O(p√{ε}),
where 0 < ε < < 1 denotes the critical
parameter and p the order of the splitting method, is
confirmed by a numerical example for the time-dependent
Gross-Pitaevskii equation.
-
Yuri Latushkin (Columbia, Missouri): Birman-Schwinger operators and the Evans function
2010/07/19, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
This is a review of some recent work related to the spectral
theory of the Birman-Schwinger type integral operators
familiar from quantum mechanics, and the Evans function, a
popular tool in stability analysis of traveling waves. Some
formulas are given relating the Evans function and its
derivative and the modified Fredholm determinants of the
respective Birman-Schwinger operators.
-
Günter M. Ziegler (TU Berlin): A strictly colored Tverberg theorem
2010/07/15, 16:15, V3-201, Mathematical Colloquium
Abstract: In autumn 1964 the young norwegian
mathematician Helge Tverberg sitting freezing in a hotel room in
Manchester proved a remarkable result: 3r-2 points in the plain can be
divided into r groups of not more then three points such that the r
triangles, lines and points have a common intersection point. One
point less is not enough. Also, a d-dimensional version of this
theorem was proven with (d+1)(r-1)+1 points.
In 1992, Vrecica and Zivaljevic presented a "colored Tverberg theorem".
Elegant topological methods and combinatorial structures
are used for the proof. Nevertheless, the result was not sharp -
Vrecica and Zivaljevic needed more points than expected.
Now there is progress: A new and surprising sharp colored version of the
original theorem of Tverberg has arised, together with new proof
methods. This is the subject of the talk.
(Joint work with Pavle V. M. Blagojevic and Benjamin Matschke
-
Alexander Ostermann (Innsbruck): Numerical analysis of operator splitting methods
2010/07/12, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Splitting methods form a large class of competitive
time discretisations of evolution equations. The reason for their
frequent use is that the splitting procedure yields time stepping
schemes which dramatically reduce the required computational effort,
compared to schemes based on the full vector field.
After a brief introduction to the concept of splitting and the
non-stiff convergence theory, we concentrate on problems with
unbounded operators. It turns out that the non-stiff order conditions
are sufficient to get optimal convergence orders for exponential
splitting methods in the stiff case. We discuss analytic frameworks
for proving (optimal) convergence results, and we introduce a new
setting that is applicable for a wide variety of linear equations and
their dimension splittings. In particular, we analyse parabolic
problems with homogeneous Dirichlet or Neumann boundary conditions on bounded domains.
We further discuss a new class of splitting methods of orders up to
fourteen based on complex coefficients. These results resolve the open
question whether there exist splitting schemes with convergence rates
greater than two in the context of analytic semigroups. As a concrete
application we consider once more parabolic equations and their
dimension splittings. The sharpness of our theoretical error bounds is
illustrated by numerical experiments.
-
Caren Tischendorf (Köln): Solution Approaches for Abstract Differential-Algebraic Equations
2010/07/05, 16:15, V5-148, Seminar Numerical Analysis
Abstract:
The simulation of complex systems describing different physical
effects becomes more and more of interest in various
applications, for instance, in chip design, in structural mechanics,
in biomechanics and in medicine. The modeling of complex
processes often lead to coupled systems that are composed of
ordinary differential equations (ODEs), differential-algebraic
equations (DAEs) and partial differential equations (PDEs).
Such coupled systems can be regarded in the general framework of
abstract differential-algebraic equations of the form
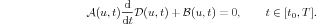
This equation is to be understood as an operator equation with
operators 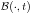 , , 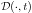 and and 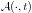 acting in real Hilbert spaces where acting in real Hilbert spaces where
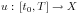 is the solution belonging to a problem
adapted space. is the solution belonging to a problem
adapted space.
If the Hilbert spaces are chosen to be the finite dimensional
space Rm, then we obtain a differential-algebraic
equation. Choosing  and and  as the natural
embedding operators, we obtain an evolution equation. If,
additionally, as the natural
embedding operators, we obtain an evolution equation. If,
additionally,  is a second-degree differential operator
in space, it leads to a parabolic differential equation. For
elliptic differential equations, the operators is a second-degree differential operator
in space, it leads to a parabolic differential equation. For
elliptic differential equations, the operators  and and
 are identically zero. are identically zero.
For most coupled systems, the operators  and and  are neither identically zero nor invertible on the time interval
[t0,T].
A general theory of abstract differential-algebraic equations
(ADAEs) does not exist and can not be expected to be given
considering alone the complexity of problems simulating partial
differential equations. However, special classes of ADAEs have
recently been successfully analyzed and simulated.
are neither identically zero nor invertible on the time interval
[t0,T].
A general theory of abstract differential-algebraic equations
(ADAEs) does not exist and can not be expected to be given
considering alone the complexity of problems simulating partial
differential equations. However, special classes of ADAEs have
recently been successfully analyzed and simulated.
In particular, we discuss solvability and perturbation results via
two different approaches. The first one addresses linear ADAEs with
constant coefficients using Laplace transformation. The second one
handles linear ADAEs with monotone, time dependent coefficients by
a Galerkin approach.
-
Christian Kuehn (Cornell): Multiple Time-Scale Dynamics: Bifurcations,
Manifolds and Mixed-Mode Oscillations
2010/06/14, 16:15, V5-148, Seminar Numerical Analysis
Abstract: We start with an introduction to fast-slow
systems. The geometric viewpoint of the theory will be
emphasized. Then we discuss the three-dimensional FitzHugh-Nagumo
(FHN) equation and its bifurcations. The singular limit bifurcation
diagram of the FHN equation will be derived. The computation and
interaction of different types of invariant manifolds will be
emphasized to explain the dynamics. We shall also briefly look at
mixed-mode oscillations (MMOs) in the FHN equation and more general
fast-slow system.
-
Dimitri Puhst (TU Berlin): Fractional derivatives and their applications
2010/06/11, 14:15, V5-148, Seminar Numerical Analysis
-
Jens Rademacher (CWI Amsterdam): Mechanisms of semi-strong interaction in multiscale reaction diffusion systems
2010/06/07, 16:15, V5-148, Seminar Numerical Analysis
Abstract: In spatial multiscale reaction diffusion systems where
some diffusion lengths are much shorter than the rest, interfaces
can form where only the components with the short scale
localise. The interaction between such interfaces is called
semi-strong as it is driven by the nonlocalised components. Cases
where the interface motion is of the order of the square of the
short diffusion lengths ('second order') have been studied over
the past decade. By formal expansions and numerical studies we
show that the interaction strength can also be of the same order
as the short diffusion length ('first order').
We illustrate these mechanisms in the Schnakenberg model and
investigate interaction manifolds and their stability. Taking a
model independent point of view, starting only from a dichotomy in
diffusion lengths, characteristic equations of motion of
interfaces for first and second order semi-strong interaction can
be derived. For first order pulse interaction with a single long
diffusion length and under certain natural assumptions several
explicit Lyapunov-functionals such as the largest interpulse
distance are found.
This is partly joint work with J. Ehrt and M. Wolfrum (WIAS, Berlin).
-
Mario Botsch (Bielefeld): Polyhedral Finite Elements
2010/05/31, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Finite element simulations of deformable objects are
typically based on spatial discretizations using either tetrahedral or
hexahedral elements. This allows for simple and efficient
computations, but in turn requires complicated remeshing in case of
topological changes or adaptive simulations. In this talk I will show
how arbitrary polyhedral elements can be used in FEM simulations,
thereby avoiding the need for remeshing (and thus simplifying)
adaptive refinement, interactive cutting, and fracturing of the
simulation domain.
-
Rolf Dieter Grigorieff (TU Berlin): Qualocation of periodic pseudo-differential operators
2010/05/03, 16:15, V5-148, Seminar Numerical Analysis
Abstract: Qualocation denotes a discretization
scheme going back to I. Sloan located somewhere between the collocation method
and the Petrov-Galerkin method. The talk covers the convergence
analysis of the method applied to periodic pseudo-differential
operators using splines with multiple vertices as an ansatz- and test
space. This analysis is based on approximation properties of the also introduced
spline spaces. We focus on a proper parameter choice providing an
additional order of convergence.
-
Jussi Behrndt (TU Berlin): Spectral properties of a class of elliptic
differential operators on bounded and unbounded domains
2010/04/22, 17:15, V3-201, Mathematical Colloquium
Abstract: In this lecture we consider a formally symmetric second order elliptic
differential expression L on a bounded or unbounded domain Ω with
smooth boundary ∂Ω. Our aim is to describe the spectral
properties of a family of selfadjoint realizations of L in
L2(Ω) with nonlocal boundary conditions on
∂Ω. For this we apply boundary triplet and
Dirichlet-to-Neumann techniques, as well as general perturbation
methods from abstract operator theory.
-
Mechthild Thalhammer (Innsbruck): High-order time-splitting spectral methods for nonlinear Schrödinger equations
2010/02/22, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk, I will address the issue of efficient
numerical methods for the time integration of nonlinear
Schrödinger equations. As model problems, I will consider systems
of coupled Gross-Pitaevskii equations that arise in quantum physics
for the description of multi-component Bose-Einstein condensates. My
intention is to study the quantitative and qualitative behaviour of
high-accuracy discretisations that rely on time-splitting Fourier and
Hermite spectral methods. In particular, this includes a stability and
convergence analysis of high-order exponential operator splitting
methods for evolutionary Schrödinger equations. Numerical
examples illustrate the theoretical results.
-
Aneta Wróblewska (Warsaw): Unsteady flows of nonhomogeneous
non-Newtonian incompressible fluids with growth conditions in
Orlicz spaces
2010/01/25, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Our purpose is to show existence of weak solutions to
unsteady flow of non-Newtonian incompressible nonhomogeneous
fluids with nonstandard growth conditions of the stress tensor. We
are motivated by the fluids of strongly inhomogeneous behavior and
characterized by rapid shear thickening. Since we are interested
in flows with the rheology more general then power-law-type, we
describe the growth conditions with help of general x-dependent
convex function and formulate our problem in generalized Orlicz spaces.
-
Jos Gesenhues (Bremen): The Kuramoto model: Modelling, analysis
and simulation
2010/01/11, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
The Kuramoto model is a model describing the behavior of a large
number of weakly coupled oszillators. In particular, synchronization
phenomena can be studied with it. In this work the classical discrete
Kuramoto model is modeled and analyzed as well as a continous ansatz
leading to a partial nonlinear integro-differential equation. The
central result of the analysis is a critical coupling value, from
which on synchronization occurs. This will be verified for both models
by simulation.
-
David Šiška (London): Finite-Difference Approximations for Normalized Bellman Equations
2010/01/11, 10:15, U5-133, Seminar Numerical Analysis
Abstract: A class of stochastic optimal control problems involving optimal stopping is considered. Methods of Krylov (Appl. Math. Optim. 52(3):365-399, 2005) are adapted to investigate the numerical solutions of the corresponding normalized Bellman equations and to estimate the rate of convergence of finite difference approxi- mations for the optimal reward functions.
-
Christopher Hartleb (TU Ilmenau): Lower bounds for the independence number
of a graph in terms of the numbers of vertices and edges
2009/12/22, 10:15, V4-119, Seminar Numerical Analysis
-
Volker Mehrmann (TU Berlin / MATHEON): Theory and numerical methods for the
stability analysis of differential algebraic systems
2009/12/14, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Lyapunov and exponential dichotomy spectral theory is
extended from ordinary differential equations (ODEs) to nonautonomous
differential-algebraic equations (DAEs). By using orthogonal changes
of variables, the original DAE system is transformed into appropriate
condensed forms, for which concepts such as Lyapunov exponents, Bohl
exponents, exponential dichotomy and spectral intervals of various
kinds can be analyzed via the resulting underlying ODE. Some essential
differences between the spectral theory for ODEs and that for DAEs are
pointed out. It is also discussed how numerical methods for computing
the spectral intervals associated with Lyapunov and Sacker-Sell
(exponential dichotomy) can be extended from those methods proposed
for ODEs. Some numerical examples are presented to illustrate the
theoretical results.
-
Arjen Doelmann (Leiden): Busse balloons and Hopf dances, or:
Bifurcations of Spatially Periodic Patterns
2009/12/07, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
In this talk we propose to study generic aspects of the Busse balloon
associated to spatially periodic patterns in reaction-diffusion equations.
The Busse balloon -- named after the physicist Friedrich Busse -- is
defined as the region in (wave number, parameter space) for which stable
periodic patterns exist; the boundary of the Busse balloon is determined
by bifurcations/destabilizations. After a general introduction, in which
we interpret the Turing bifurcation and the associated side band
instability mechanism, as a well-studied and well-understood generic
aspect of the Busse balloon, we introduce a novel destabilization
mechanism for reversible spatially periodic patterns. This Hopf dance
mechanism occurs for long wavelength patterns near the homoclinic tip of a
Busse balloon. Here, the boundary of the Busse balloon locally has a
fine-structure of two intertwining ?dancing? Hopf destabilization curves
(or manifolds) that limit on the Hopf bifurcation value of a homoclinic
limit pulse.
-
Thorsten Hüls: On r-periodic orbits of k-periodic maps
2009/11/30, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk, we analyze r-periodic orbits of k-periodic
difference equations, i.e.
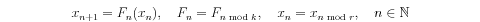
and their stability.
We discuss that, depending on the values of r and k,
such orbits generically only occur in finite dimensional
systems that depend on
sufficiently many parameters, i.e. they have a large codimension in
the sense of bifurcation theory.
As an example, we consider the periodically forced Beverton-Holt model,
for which explicit formulas for the globally attracting periodic orbit,
having the minimal period k=r, can be derived.
When r factors k the Beverton-Holt model with two
time-variant parameters is an example that can be studied explicitly and
that exhibits globally attracting r-periodic orbits. For
arbitrarily chosen periods r and k,
we develop an algorithm for the numerical approximation
of an r-periodic orbit and of
the associated parameter set, for which this orbit exists.
We apply the algorithm to the generalized
Beverton-Holt and another example
that exhibits periodic orbits with r and k relatively prime.
-
Georgy Kitavtsev (WIAS Berlin): Reduced ODE models describing coarsening dynamics
of slipping droplets
2009/11/23, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk the topic of reduced ODE models corresponding to a family of
one-dimensional lubrication equations derived by Münch et al. 06' is
addressed. This family describes the dewetting process of nanoscopic thin
liquid films on hydrophobized polymer substrates due to the presence of
several intermolecular forces and takes account of different ranges of
slip-lengths at the polymer substrate interface. Reduced ODE models derived
from underlying lubrication equations allow for an efficient analytical and
numerical investigation of the latest stage of the dewetting process:
coarsening dynamics of the remaining droplets. We first give an asymptotical
derivation of these models and use them to investigate the influence of
slip-length on the coarsening dynamics. In a so called strong-slip case we
find a unique critical slip-length at which the direction for migration of
droplets changes. In the second part of the talk we present a new geometric
approach which can be used for an alternative derivation and justification of
above reduced ODE models and is based on a center-manifold reduction recently
applied by Mielke and Zelik 08' to a certain class of semilinear parabolic
equations. One of the main problems for a rigorous justification of this
approach is investigation of the spectrum of a lubrication equation
linearized at the stationary solution, which describes physically a single
droplet. The corresponding eigenvalue problem turns out to be a singularly
perturbed one with respect to a small parameter ε tending to zero. For this problem we show existence of an
ε-dependent spectral gap between a unique
exponentially small eigenvalue and the rest of the spectrum.
-
Sergei Pilyugin (St. Petersburg): Lipschitz shadowing property
2009/11/09, 14:15, V5-148, Seminar Numerical Analysis
-
Dario Götz (TU Berlin): Existence of weak solutions and time
discretization of the equation of motion for generalized non-Newton fluids
2009/10/19, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Non-Newton fluids behave, typically due
to underlying microstructures, different than we expect from ordinary
fluids; e.g. blood, lava, color, tomato ketchup, polymeres, emulsions
or suspensions.
In this talk we analyze the existence of weak solutions of the
non-stationary equation of motion for incompressible fluids with shear
rate dependent viskosity and p-structure for the stress tensor. In the
case  the existence of weak solutions follows from the theory
of monotone operators. The more interesting case, that we focus on
here, is p < 2. We aim to show the existence of a weak solution of
the problem for all the existence of weak solutions follows from the theory
of monotone operators. The more interesting case, that we focus on
here, is p < 2. We aim to show the existence of a weak solution of
the problem for all
 . A problem that occurs is the missing regularity of the
time derivations of the solution. . A problem that occurs is the missing regularity of the
time derivations of the solution.
The idea of the proof is based on a time discretization by the
implicit Euler method. Using the so-called Lipschitz truncation method
and proper regularities of the Sobolev spaces the problem of the
missing regularity can be solved. A representation of the pressure
vanishing in the weak formulation comes along with this ansatz and is
essential for the idea of the proof.
-
Arnulf Jentzen (Frankfurt): Taylor expansions for stochastic
partial differential equations
2009/07/24, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Taylor expansions of stochastic partial
differential equations (SPDEs) of evolutionary type
and their first applications to numerical analysis
are presented. The key instruments for
deriving such Taylor expansions are the semigroup
approach, i.e. to understand the SPDE as a mild
integral equation, and an appropriate recursion
technique.
-
David Speer (Bielefeld): Directing Brownian Motion in Periodic Potentials
2009/07/03, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We consider a single Brownian particle
subjected to periodic and symmetric potentials. Directed particle
transport can be achieved only by breaking symmetry, such as applying
a constant force. Usually, particle transport is in the direction of
that force, in line with the second law of thermodynamics. In
non-equilibrium, this behaviour may be drastically different due to a
subtle interplay of deterministic chaos, symmetry and stochastic
forces. This may be exploited to achieve almost complete control of
transport direction, even transport directly against that force
(negative absolute mobility) [1]. Recently, the effect was observed
experimentally for Josephson junctions [2].
[1] D. Speer et al., Europhys. Lett. 79, 10005 (2007), D Speer et al.,
Phys. Rev. Lett. 102, 124101 (2009)
[2] J. Nagel et al., Phys. Rev. Lett. 100, 217001 (2008)
-
Lutz Angermann (Clausthal): Rosenbrock method for PDAEs
2009/06/19, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Mathematical modelling of various
problems in science, engineering, medicine etc. lead to (in general
nonlinear) equation systems consisting of coupled equations of
different kinds, e.g. parabolic, elliptic and ordinary differential
equations and algebraic equations. Such systems are called partial
differential equations (PDAEs).
In the development of numerical methods for the solution of such systems
via the vertical line method (spatial discretization first) a set of
new questions arise when we try to transfer methods for differential
algebraic equation of moderate size to the evolving (ordinary)
differential algebraic equations (called MOL-DAEs). In this talk these
questions - together with adequate solution approaches - will be presented.
-
Mario Ohlberger (Münster): Reduced basis techniques for
parametrized nonlinear evolution equations
2009/05/15, 14:15, V5-148, Seminar Numerical Analysis
Abstract: In this talk we will present the
reduced basis method for the efficient computation of
parametrized evolution equations. The method allows an
offline/online partition of the solution process. First in an
offline phase a reduced basis space, adapted to the concrete problem, is generated by means of
Finite Element or Finite Volume methods. After that we can
derive - independent of the complexity of the underlying Finite
Element of Finite Volume method - very fast simulation results
for any parameter variations.
-
Hans-Georg Purwins (Münster): Localized solutions to the extended
FitzHugh-Nagumo equation
2009/05/07, 12:30, V3-201, FSPM Colloquium
Abstract: Self-organized dissipative structures
play in important role in nature and engineering. Many scientists
believe that the understanding and application of them is one of the
biggest challenges of modern science. This talk deals with such
structures in form of solitary localized spots, also called
'dissipative solitons' (DS). These objects show particle-like behavior
in many ways and can be observed both in experiments and as solutions
of reaction diffusion systems of FitzHugh-Nagumo type.
In the first part of the talk the occurence of DS is presented by
means of experimental electrical transport systems, e.g. as stationary
and travelling isolated pulses, as stationary travelling and rotating
'molecules' and as 'cristalline', 'fluid' and 'gaseous' multi-particle
systems. The occuring interaction phenomena cover spreading and
clustering as well as generation and annihilation. Numerical
experiments show that all experimental observations can be described
by the generalized FitzHugh-Nagumo equation. It turns out that this
equation can be seen as a 'normal form' for a bigger universality
class of DS carrying systems.
In the second part it will be shown how under certain assumptions
particle equations, which describe the dynamical behavior of weak
interacting DS very well, can be derived from the generalized FitzHugh-Nagumo
equation.
-
Christian Wieners (Karlsruhe): Efficient numerical methods in elastoplasticity
2008/07/11, 14:15, V2-210, Seminar Numerical Analysis
Abstract: The talk begins with illustrating the
classical model of Prandtl Reuß plasticity and efficient
numerical methods for the solution of the discrete finite element
problem will be presented.
As these problems are in general ill-conditioned or even ill-posed,
robust methods are needed. In particular modern methods will be
discussed based on optimization concepts (non-smooth newton methods,
SQP methods).
In the second part of the talk recent applications are presented, The
classical models can be regularized using infinitesimal rotations or
gradients of plastic distortion (joint work with P. Neff,
Darmstadt). It will be shown, that numerical methods can be applied
to the extended models. Finally the efficience of the methods will be
demonstrated in a parallel simulation of an elastoplastic soil
mechanic model (joint work with W. Ehlers, Stuttgart).
-
Peter Giesl (Sussex): Determination of the Basin of Attraction of Equilibria and
Periodic Orbits
2008/07/10, 14:15, V2-210, Seminar Numerical Analysis
Abstract: The basin of attraction of equilibria or
periodic orbits of an autonomous ODE can be determined through
sublevel sets of a Lyapunov function. To construct such a Lyapunov
function, i.e. a scalar-valued function which is decreasing along
solutions of the ODE, a linear PDE is solved approximately using
Radial Basis Functions. Error estimates ensure that the approximation
itself is a Lyapunov function.
For the construction of a Lyapunov function it is necessary to know
the position of the equilibrium or periodic orbit. A different method
to analyse the basin of attraction of a periodic orbit without
knowledge of its position is Borg's criterion. The sufficiency and
necessity of this criterion in different settings will be discussed.
-
Fritz Colonius (Augsburg): Near Invariance and Local Transience for Perturbed Systems
2008/06/27, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Nearly invariant subsets of the state
space of a dynamical system are subsets which can only be left after
long time. For families of random diffeomorphisms one can characterize
these subsets via an associated discrete-time control system and,
also using the Perron-Frobenius operator, one can show that the exit
times are positive and polynomially unbounded.
-
Günther Grün (Erlangen): Energiemethoden zur Analyse von Benetzungsph"anomenen
2008/06/20, 14:15, V5-148, Seminar Numerical Analysis
-
Jens Lorenz (Albuquerque, New Mexico): The Brenner-Klimontovich Modifications
of the Navier-Stokes-Fourier System
2008/06/16, 14:15, V5-148, Seminar Numerical Analysis
Abstract: The classical Navier-Stokes-Fourier
equations for heat conducting compressible flows form a coupled
hyperbolic-parabolic system. The system has been criticized, on
principle grounds, as being inconsistent with non-equilibrium
thermodynamics. In this talk I consider modified systems, suggested by
Brenner and Klimontovich, which are essentially parabolic. The
modified systems distinguish between a mass velocity and a volume
velocity.
I also show some crude numerical results.
-
Gerhard Starke (Hannover): An adaptive mixed finite element method for
elastic contact problems
2008/05/23, 14:15, V5-148, Seminar Numerical Analysis
-
Wolf-Jürgen Beyn: Localization and continuation of nonlinear eigenvalues
2008/05/16, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Nonlinear eigenvalue problems are ubiquitous in the stability analysis
of nonlinear systems, such as vibrating systems or systems with delay.
Numerical discretizations then lead to large and sparse parameterized
nonlinear eigenvalue problems

where the matrix family  depends smoothly on the real parameter
depends smoothly on the real parameter 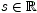 and analytically
on the eigenvalue parameter and analytically
on the eigenvalue parameter 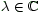 . We aim at an algorithm
that detects a small swarm of eigenvalues λ
within a prescribed complex domain and that
continues the swarm with respect to the parameter s. . We aim at an algorithm
that detects a small swarm of eigenvalues λ
within a prescribed complex domain and that
continues the swarm with respect to the parameter s.
A new localization procedure is presented that determines the eigenvalues
(and eigenvectors) in the interior of a smooth
contour of the complex plane. The method builds on Cauchy's integral formula
and on a theorem of Keldysh.
Then we discuss a continuation method that pursues the swarm of eigenvalues
with the parameter and that deflates and inflates the swarm when collisions
with outside eigenvalues occur.
-
Tycho van Noorden (Eindhoven): Crystal dissolution and precipitation in porous media: formal homogenization and numerical experiments
2008/05/09, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We investigate a two-dimensional
micro-scale model for crystal dissolution and precipitation in a
porous medium. The model contains a free boundary and allows for
changes in the pore volume. Using a level-set formulation of the free
boundary, we apply a formal homogenization procedure to obtain
upscaled equations. For general micro--scale geometries, the
homogenized model that we obtain falls in the class of distributed
microstructure models. For circular initial inclusions the distributed
microstructure model reduces to system of partial differential
equations coupled with an ordinary differential equation. In order to
investigate how well the upscaled equations describe the behavior of
the micro-scale model, we perform numerical computations for a test
problem.
-
Christof Eck (Bielefeld): Asymptotics and numerical approximation of
phase field models
2008/04/18, 14:15, V5-148, Seminar Numerical Analysis
-
Etienne Emmrich (TU Berlin): Analysis of the time discretization of
evolution equations with a monotone operator by the BDF2
2008/02/20, 14:15, V5-148, Seminar Numerical Analysis
Abstract: Time-dependent processes in nature and
science can often be modelled by an initial value problem for an
evolution equation of first order with monotone main term. There are
plenty of methods for the time discretization whereas the Backward
differentiation formula 2 excels by its properties.
First the talk will give an overview of known results for linear and
semilinear problems on both equidistant and variable time grids. Then
well-posedness, a-priori estimates, convergence of piecewise
polynomial prolongations, stability and error estimates in case of
constant time stepsize are studied for an evolution equation with
monotone operator and reinforced continous noise. A special algebraic
identity turns out to be fundamental, from which also the G-stability
of the method follows. In the end the case of variable stepsizes will
be discussed.
-
Peter Benner (TU Chemnitz): Control-oriented model reduction for parabolic systems
2008/01/25, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We will discuss model reduction techniques for the control of dynamical
processes described by parabolic partial differential equations from a
system-theoretic point of view.
The methods considered here are based on spatial semi-discretization of
the PDE followed by balanced truncation techniques applied to the
resulting large-scale system of ordinary differential equations.
Several choices of the system Gramians that are used for balancing
will be presented.
We will discuss open-loop and closed-loop techniques that
allow to preserve system properties important for controller design.
Furthermore we will discuss an error estimate based on a combination
of FEM and model reduction error bounds. We will also discuss how the
state of the full-order system can be recovered from the reduced-order
model. Several numerical examples will be used to demonstrate the
proposed model reduction techniques.
-
Barnabas Garay (TU Budapest): Chaos Detection by Computer
2008/01/21, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We report on experiences with an adaptive subdivision method supported by
interval arithmetic that enables us to prove subset relations for certain
mappings associated with the dynamics and thus to check certain sufficient
conditions for chaotic behaviour in a rigorous way.
Our proof of the underlying abstract theorem avoids of referring to any
results of applied algebraic topology and relies only on the Brouwer fixed
point theorem.
The second novelty is that the process of gaining the subset relations to be
checked is, to a large extent, also automatized. The promising subset
relations come from solving a constrained optimization problem via the
penalty function approach.
Abstract results and computational methods are demonstrated by finding
planar subsets with chaotic behaviour for iterates of the classical Henon
mapping as well as for the time-T-map of the solution operator to a damped
pendulum equation with T-periodic forcing.
-
Alexander Dressel (Stuttgart): Existence, uniqueness and time-asymptotic behaviour of weak solutions
for a viscoelastic two-phase model with nonlocal capillarity
2008/01/11, 14:15, V5-148, Seminar Numerical Analysis
Abstract: The aim of this talk is to study the
existence, uniqueness and time-asymptotic behaviour of solutions of an
initial-boundary value for a viscoelastic two-phase material with
capillarity in one space dimension. Therein, the capillarity is
modelled via a nonlocal interaction potential. The existence proof
relies on uniform energy estimates for a family of difference
approximations: with these estimates at hand we show the existence of
a global weak solution. By means of a nontrivial variant of existing
arguments in the literature (the so-called "Andrews-trick") ,
uniqueness and further regularity are proven.Then, based on the
existence and regularity results, we prove the time-asymptotic
convergence of the strain-velocity field.
-
Anton Arnold (TU Wien): Open boundary conditions for wave diffusion
problems in unbounded domains
2007/12/19, 15:00, V5-148, Seminar Numerical Analysis
Abstract: Partial differential equations on
unbounded domains occur in a natural way in acoustic, quantum mechanic
and fluid mechanic problems. But the numerical simulation has
to constrain on finite subdomains - by the introduction of
(artificial) absorbing boundary conditions.
In this talk we will give an overview of such strategies, and will
discuss especially their application to the time-dependent Schrödinger equation in 1D
and 2D (stripes and circular geometry).
-
Heinrich Voß (TU Hamburg-Harburg): Numerical methods for sparse nonlinear eigenvalue problems
2007/12/14, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We consider the nonlinear eigenvalue
problem
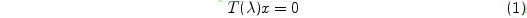
where 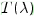 is a family of sparse matrices. Problems of
this type arise in damped vibrations of structures,
conservative gyroscopic systems, lateral buckling problems,
fluid-solid vibrations, and the electronic behaviour of quantum
dot heterostructures, to name just a few. is a family of sparse matrices. Problems of
this type arise in damped vibrations of structures,
conservative gyroscopic systems, lateral buckling problems,
fluid-solid vibrations, and the electronic behaviour of quantum
dot heterostructures, to name just a few.
We discuss iterative projection methods of Jacobi-Davidson and
Arnoldi type which are particularly efficient if the
eigenvalues of (1) satisfy a minmax property. Moreover,
we present a variant of the automated multi-level
substructuring for nonlinear problems.
-
Olaf Steinbach (TU Graz): Boundary Integral Equations: Analysis and Applications
2007/12/07, 14:15, V5-148, Seminar Numerical Analysis
-
Kathrin Schreiber (TU Berlin): Nonlinear Rayleigh functionals
2007/11/23, 14:15, V5-148, Seminar Numerical Analysis
Abstract: After a short introduction on nonlinear eigenvalue problems, defined by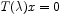 where where 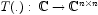 is a matrix-valued mapping, we review Rayleigh quotients for Hermitian
and general matrices and introduce appropriate {\em Rayleigh
functionals} p(u) and p(u, v) defined by
is a matrix-valued mapping, we review Rayleigh quotients for Hermitian
and general matrices and introduce appropriate {\em Rayleigh
functionals} p(u) and p(u, v) defined by
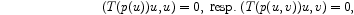
for nonlinear eigenvalue problems, where u, v are approximations for
right and left eigenvectors. Local existence and uniqueness of p is
shown as well as 'stationarity' (technically p is not
differentiable). Bounds for the distance of p and the exact eigenvalue
are provided, which are of the same order as in the linear case.
The last part of the presentation includes numerical results, where
the emphasis lies on complex symmetric problems, where the application
of the symmetric Rayleigh functional gives considerably better results
associated with an Jacobi-Davidson type method compared to the
standard Jacobi-Davidson method.
-
Helmut Podhaisky (Halle): Two-step peer methods for time-dependent
partial differential equations
2007/10/19, 14:15, V5-148, Seminar Numerical Analysis
Abstract: There are two classes of methods for the numerical solution of initial
value problems: linear multi-step methods, e.g. of the BDF type, on
the one hand and Runge-Kutta methods on the other hand. Advantages and
disadvantages are well-known: small costs per step for multi-step
methods, excellent stability properties for Runge-Kutta methods. Is it
possible to combine both advantages? The answer is 'yes' (or 'yes,
possibly'), we just have to look at general linear methods (GLMs),
i.e. multi-level multi-step methods.
In this talk we present peer methods which compute s approximations 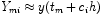 ,
i=1,...,s in a diagonal implicit scheme ,
i=1,...,s in a diagonal implicit scheme
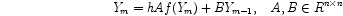 . .
The order conditions are given by the Taylor expansion. The more
difficult task is to ensure stability, particularly A-stability, and
to optimize the remaining free parameters in such a way that the
methods work robust.
In the end of the talk peer methods up to order 4 are used in FEM code
KADOS to solve partial differential equations.
-
Arnd Scheel (Minnesota): Periodic patterns: perturbation, modulation
and bifurcation
2007/10/12, 14:15, V5-148, Seminar Numerical Analysis
-
Thorsten Hüls: Numerical approximation of homoclinic trajectories for
non-autonomous maps
2007/05/09, 14:15, V5-148, Seminar Numerical Analysis
Abstract: For time-dependent dynamical systems of the form
homoclinic trajectories are the non-autonomous analog of
homoclinic orbits from the autonomous world.
More precisely, two trajectories (xn)n ∈
Z, (yn)n ∈ Z of (1) are called homoclinic to each other, if
We introduce two boundary value problems, the solution of which yield
finite approximations of these trajectories. Under certain dichotomy
and transversality assumptions, we prove existence, uniqueness and
error estimates. Finally, the method and the error estimates are
illustrated by an example.
-
Sergei Pilyugin (St. Petersburg): Dynamics of some mappings determined by piecewise linear functions
2007/04/25, 14:15, V5-148, Seminar Numerical Analysis
Abstract: We study dynamics of multidimensional
mappings that are determined by scalar functions. Such mappings arise,
for example, when we discretize a semilinear parabolic equation. If
the determining scalar function is piecewise-linear (with a finite
number of "corner" points), then the dynamics is described by a finite
number of parameters, and approaches of "discrete nature" are
applicable.
-
Jörg Härterich (FU Berlin): Convergence to Rotating Waves in Spatially Inhomogeneous Balance Laws
2007/04/11, 14:15, V5-148, Seminar Numerical Analysis
Abstract: I will study the long-time behaviour of scalar balance
laws where the source term is space-dependent. It turns
out that under some assumptions solutions exist which
converge to rotating waves. After explaining the proof
of this statement I will discuss which role these
rotating waves play within the global attractor. In
addition, some remarks concerning the effect of small
viscosity and the case where the assumptions are
violated, will be presented.
-
Daniel Holtz (Bielefeld): Überlappender Schwarz-Algorithmus
für nichtlineare Konvektions-Probleme
2006/12/20, 12:30, V3-201, Seminar Numerical Analysis
Abstract: Der Schwarz-Algorithmus wird verwendet,
um Randwertprobleme mit Hilfe von Gebietszerlegungen numerisch
parallel zu berechnen. Der Vortrag stellt eine Realisierung dieses
Algorithmus vor. Im eindimensionalen Fall wird für parabolische
nichtlineare Differentialgleichungen Konvergenz des Algorithmus
bewiesen und numerisch überprüft. Viele Parameter des
Algorithmus sind vom Anwender frei wählbar. Basierend auf der
Wahl der Randwerte für die Teilgebiete wird eine Verbesserung des
Algorithmus vorgestellt.
-
Marcel Oliver (Bremen): Subgrid closures for passive advection
through nonreflecting boundary conditions in Fourier space
2006/12/13, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
We consider the evolution of a passive scalar in a shear flow in its
representation as a system of lattice differential equations in wave
number space. When the velocity field has small support, the
interaction in wave number space is local and can be studied in terms
of dispersive linear lattice waves. We close the restriction of the
system to a finite set of wave numbers by implementing transparent
boundary conditions for lattice waves. This closure is studied
numerically in terms of energy dissipation rate and energy spectrum,
both for a time-independent velocity field and for a time-dependent
synthetic velocity field whose Fourier coefficients follow independent
Ornstein-Uhlenbeck stochastic processes.
-
Martin Rasmussen (Augsburg): Morse partitions of non-autonomous dynamical systems
2006/12/06, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
Das globale asymptotische Verhalten dynamischer Systeme auf kompakten
metrischen Räumen läßt sich mittels Morse-Zerlegungen
beschreiben. Deren Komponenten, die so genannten Morse-Mengen,
erhält man als Schnitte von Attraktoren und Repeller. In diesem
Vortrag werden spezielle Begriffe von Attraktoren und Repeller
für nichtautonome dynamische Systeme eingeführt, die
geeignet für eine nichtautonome Verallgemeinerung der
Morse-Zerlegungen sind. Die dynamischen Eigenschaften dieser
Morse-Zerlegungen werden diskutiert; besonderes Augenmerk wird hierbei
auf eindimensionale und lineare Systeme gelegt.
-
Malte Samtenschnieder: Periodische Orbits zeitdiskreter
nicht-autonomer dynamischer Systeme und ihre Stabilitätseigenschaften
2006/11/08, 14:15, U2-205, Seminar Numerical Analysis
Abstract: Ausgehend vom autonomen Fall, stehen in diesem Vortrag
periodische Orbits nicht-autonomer dynamischer Systeme im
Mittelpunkt. Für natürliche Zahlen 2 ≤ r < k betrachten wir -
statt für festes F - für eine zeitlich veränderliche k-periodische
Funktionenfamilie {Fn}n ∈ Z so genannte r-Zykel
cr, für die wir eine Stabilitätsanalyse durchführen. Mit Hilfe
eines Satzes, der im nicht-autonomen Fall den Zusammenhang zwischen
der Stabilität eines Fixpunkts und der Stabilität eines Zykels
herstellt, zeigen wir: Wenn cr für das betrachtete nicht-autonome
dynamische System global asymptotisch stabil ist, folgt, dass r ein
Teiler von k ist. In dieser speziellen Situation approximieren wir
r-periodische Orbits k-periodischer Funktionenfamilien mit Hilfe
eines auf einer Fixpunktgleichung basierenden Lösungsverfahrens.
Ausgehend vom periodischen Beverton-Holt-Modell und der periodischen
Stiletto-Abbildung geben wir numerische Ergebnisse an, deren
Stabilität wir ebenfalls untersuchen. Abschließend skizzieren wir,
welche Probleme auftreten, wenn wir die Bedingung, dass r ein Teiler
von k ist, fallen lassen. Wir begründen, warum wir dann allgemein
keine Lösung angeben können.
-
Anke Mayer-Bäse (Florida): Challenges in Computational Intelligence: From Neurodynamics to Medical Imaging
2006/07/12, 14:15, V5-148, Seminar Numerical Analysis
-
Clarence Rowley (Princeton): Template-based methods for model reduction and control of systems with symmetry
2006/07/05, 14:15, V5-148, Seminar Numerical Analysis
-
Thorsten Hüls: Non-autonomous difference equations and bifurcations
2006/06/28, 14:15, V5-148, Seminar Numerical Analysis
-
Janosch Rieger: Numerical grid methods for differential inclusions
2006/05/31, 14:15, V5-148, Seminar Numerical Analysis
-
Renate Winkler (HU Berlin): Stochastic DAEs in Circuit Simulation
2006/05/24, 14:15, V5-148, Seminar Numerical Analysis
-
Jens Rademacher (WIAS Berlin): Computing absolute and essential spectra using continuation
2006/05/17, 14:15, V5-148, Seminar Numerical Analysis
-
Daniel Kressner (TU Berlin): Structured eigenvalue problems
2006/05/10, 14:15, V5-148, Seminar Numerical Analysis
-
Vera Thümmler: How to freeze traveling waves without losing stability
2006/05/03, 14:15, V5-148, Seminar Numerical Analysis
-
Alexander Lust: A hybrid method for the computation of Liapunov exponents
2006/04/26, 14:15, V5-148, Seminar Numerical Analysis
-
Sergei Pilyugin (St. Petersburg): Sets of dynamical systems with various limit shadowing properties
2006/04/12, 14:15, V5-148, Seminar Numerical Analysis
-
Simon Malham (Edinburgh): Efficient strong integrators for linear stochastic systems
2006/03/17, 14:15, V5-148, Seminar Numerical Analysis
-
Sergey Piskarev (Bielefeld, Moskau): Maximal regularity for parabolic and elliptic problems
2006/01/25, 14:15, V5-148, Seminar Numerical Analysis
-
Andreas Münch (HU Berlin): Non-classical shock solutions and other issues in thin film problems
2006/01/11, 14:15, V5-148, Seminar Numerical Analysis
-
Alexander Dressel (Heidelberg): Existence of smooth shock profiles for hyperbolic balance laws
2005/12/14, 14:15, V5-148, Seminar Numerical Analysis
-
Jens Rottmann-Matthes: Spectral properties of mixed
hyperbolic-parabolic systems
2005/07/22, 14:15, V5-148, Seminar Numerical Analysis
-
Abigail Wacher (Frankfurt): Solving PDE's with weighted moving finite elements
2005/06/08, 14:15, V5-148, Seminar Numerical Analysis
-
Caren Tischendorf (TU Berlin): Stability preserving integration of DAEs
2005/02/02, 14:15, V5-148, Seminar Numerical Analysis
-
Sergey Piskarev (Twente,Moskau): On the approximation of attractors
2005/01/26, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
We consider semilinear problems of the form
u' = Au + f(u), where A generates an exponentially decaying compact
analytic semigroup in a Banach space E and f is globally
Lipschitz and bounded map from Eα into E
(Eα=D((-A)α) with the graph norm). These assumptions
ensure that the problem has a global attractor. Under a very
general approximation scheme we prove that the dynamics of such
problem behaves upper semicontinuously.
We also prove that, if all equilibrium solutions of this problem
are hyperbolic, then there is an odd number of such equilibrium
solutions. Additionally, if we impose that every global solution
converges as t → ± ∞, (e.g. gradient semigroups with
isolated equilibria), then we prove that under this approximation
scheme the attractors also behave lower semicontinuously.
This general approximation scheme includes finite element method,
projection and finite difference methods. The main assumption on
the approximation is the compact convergence of resolvents which
may be applied to many other problems not related to
discretization.
-
Wilhelm Huisinga (FU Berlin): Metastability and Dominant Eigenvalues of
Transfer Operators
2004/11/25, 10:15, W0-135, Seminar study group pattern formation
Abstract:
There are many problems in physics, chemistry and biology
where the length and time scales corresponding to the
microscopic descriptions (given in terms of some stochastic or
deterministic dynamical system), and the resulting macroscopic
effects differ many orders of magnitude.
Rather than resolving all microscopic details, often one is
interested in characteristic features on a macroscopic level
(e.g., phase transitions, conformational changes of
bio-molecules, climate changes etc.). In this setting,
metastability is important macroscopic characteristic which is
related to the long time behavior of the dynamical system. It
refers to the property that the dynamics is likely to remain
within a certain part of the state space for a long period of
time, until it eventually exits and transits to some other
part of the state space.
In this talk we introduce the concept of metastability in the
setting of Markov processes, and prove upper and lower bounds
for a decomposition of the state space into metastable subsets
in terms of dominant eigenvalues and eigenvectors of a
corresponding transfer operator. The bounds are explicitly
computable and sharp. The results do not rely on any
asymptotic expansions in terms of some smallness parameter,
but rather hold for arbitrary transfer operators satisfying a
reasonable spectral condition.
-
G. Grammel (TU München): Approximations in differential
inclusions
2004/11/24, 14:15, V5-148, Seminar Numerical Analysis
-
Barnabas Garay (TU Budapest): The Miranda approach: a framework for
computer-assisted proofs of chaos
2004/11/17, 14:15, V5-148, Seminar Numerical Analysis
-
Julia Nolting: Bifurcations of periodic orbits and their
numerical computation
2004/07/21, 14:15, V5-148, Seminar Numerical Analysis
-
Stefan Siegmund (Frankfurt/Main): Time-variant linear systems
2004/07/15, 14:15, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
Abstract:
When studying nonlinear phenomena locally one can expect at most
as good understanding as in the linear theory. The behavior of
a linear differential equation xt = Ax is completely
characterized by the eigenvalues and eigenspaces of the n
x n matrix A. What mathematical concepts take
place for the eigenvalues and eigenspaces if A
varies over time caused by random, controlled or general
deterministic influences? In this talk we will follow the historical
development via Floquet, Lyapunov, Bohl, Osedelets, Sacker and
Sell, give some examples and describe the correlations and
some actual results.
-
Jerrold E. Marsden (CalTech, Pasadena): The Euler-Poincare Equations
2004/07/01, 17:15, V3-201, Mathematical Colloquium
Abstract:
The Euler-Poincare equations were born in 1901 when Poincare
made a sweeping generalization of the classical Euler equations
for the rigid body and ideal fluids. He did this by formulating
the equations on a general Lie algebra, the rigid body being
associated with the rotation Lie algebra and fluids with the Lie
algebra of divergence free vector fields. Since then, this
setting has been used for many other situations, such as the KdV
equation, shallow water waves, averaged fluid equations, and the
template matching equations of computer vision to name just a
few. This talk will give an overview of Euler-Poincare and
Lie-Poisson reduction theory (from the tangent and cotangent
bundles of a Lie Group to its Lie algebra or dual) and then
will focus on the specifics for the case of the algebra of all
vector fields. Special singular solutions will be described
which generalize the peakon (soliton) solutions of the
(Camassa-Holm-Fokas-Fuchsteiner) shallow water equations from
one to higher dimensions; the manner in which momentum maps (in
the sense of Noether's theorem from mechanics) play an important
role in these special singular solutions will be
presented. (Joint work with Darryl Holm)
-
Giovanni Samaey (Leuven): Connecting orbits in delay differential
equations: computation and application to traveling waves in
delay PDEs
2004/06/02, 14:15, V5-148, Seminar Numerical Analysis
Abstract:
Connecting orbits in delay differential equations (DDEs) are
approximated using projection boundary conditions, which
involve the stable and unstable manifolds of a steady
state. However, in contrast with ODEs, the stable manifold of
a steady state of a DDE is infinite-dimensional. We circumvent
this problem by reformulating the end conditions using a
special bilinear form. The resulting boundary value problem is
solved in the Matlab package DDE-BIFTOOL using a collocation
method. We show numerical convergence results in terms of
discretization and truncation errors, and compare these to the
ODE case.
Besides their importance for the bifurcation analysis of DDEs,
homoclinic and heteroclinic orbits arise naturally when
looking for traveling waves ofdelay partial differential
equations (delay PDEs). We show that, using DDE-BIFTOOL, we
can compute these traveling waves, as well as the rightmost
part of their spectrum. The numerical results suggest that
the spectral properties of traveling waves in delay PDEs are
comparable to properties that were proved by Sandstede for the
PDE case.
-
Imre Bozi (Budapest): Multiplicity results for the one-dimensional p-Laplacian
2004/05/26, 14:15, V5-148, Seminar Numerical Analysis
-
Bernd Krauskopf (Bristol): The saddle-node Hopf bifurcation with global reinjection
2004/02/05, 12:30, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
-
Christian Poetzsche (Augsburg): Nonautonomous Dynamics, Time Scales and Discretization
2003/12/10, 14:15, V5-148, Seminar Numerical Analysis
-
Tobias Gayer (Augsburg): Almost-invariance of diffusion processes and parameter dependent
control problems - results and numerical methods
2003/11/05, 14:15, V5-148, Seminar Numerical Analysis
-
Nils Wagner (Stuttgart): Multiple eigenvalues of parameter dependent matrix polynomials
2003/10/29, 14:15, V5-148, Seminar Numerical Analysis
-
Lars Grüne (Bayreuth): Numerics and applications of stochastic optimal control
2003/05/28, 14:15, V5-148, Seminar Numerical Analysis
-
Zou Yong-Kui (Changchun): Generalized Hopf bifurcation for non-smooth planar dynamical systems
2003/05/21, 14:15, V5-148, Seminar Numerical Analysis
-
Jens Kemper: Attractors and invariant measures in
reaction diffusion equations
2003/01/29, 14:15, V5-148, Seminar Numerical Analysis
-
Andrei Afendikov (Keldysh Institut): Numerical exterior algebra in spectral problems of stability
2002/10/24, 12:30, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
Abstract:
Spectral problems of stability on a finite or infinite
interval often lead to stiff problems that are difficult to handle
numerically. Using as an example the problem of stability for the pulse
solution to the complex Ginzburg-Landau equation it is supposed to
demonstrate how classical shooting methods can be transformed
to a modern
exterior algebra approach which leads to the investigation of
the so-called Evans function.
The numerical algorithm for evaluating the Evans function uses
explicitly the matrix representation of the Hodge star operator and the
numerical integrator that respects the Plücker imbedding of the
Grassman manifold into the space of exterior forms.
-
Eusebius J. Doedel (Concordia Univ., Montreal): Continuation of Periodic Solutions in
Conservative Systems with Application to the N-Body Problem
2002/10/02, 14:15, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
Abstract:
I will show how boundary value continuation software can be used
to compute families of stable and unstable periodic solutions of
conservative systems. A simple example will be used to illustrate
the main idea. I will show how the computational approach can be
used to follow the recently discovered figure-8 orbit of Montgomery,
Chenciner, and Simo, as the mass of one of the bodies is varied.
The numerical results show, among other things, that there exists
a continuous path from the figure-8 orbit to periodic solutions
of the restricted three body problem.
Various aspects of this work are done in cooperation with
Andre Vanderbauwhede (Gent), Don Dichmann (Aerospace Corporation),
Jorge Galan (Sevilla), and Herb Keller and Randy Paffenroth (Caltech).
-
Björn Sandstede (Ohio State Univ., Columbus): Spectral properties of spiral waves
2002/07/11, 12:30, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
-
Andreas Keese (Braunschweig): Numerical solution of systems with stochastic operator
2002/06/20, 12:30, V2-216, Seminar of the Research Group Spectral analysis, asymptotic distributions and stochastic dynamics
-
Werner Vogt (TU Ilmenau): Numerical approximation of invariant tori and quasi-periodic solutions
of dynamical systems
2002/06/07, 14:15, V5-148, Seminar Numerical Analysis
-
Kurt Lust (Leuven): Accurate computation of Floquet multipliers in multiple shooting and Gauss-Legendre codes
2002/02/13, 14:15, V5-148, Seminar Numerical Analysis
-
Arno F. Münster (Würzburg): Strukturbildung in chemischen Reaktionen mit Ionen
2001/11/22, 10:15, W9-109, Seminar study group pattern formation
-
Qin Mengzhao (Peking): Multisymplectic methods for infinite-dimensional Hamiltonian systems
2001/11/16, 14:15, U5-133, Seminar Numerical Analysis
-
Alexander Lust: Numerical computation of Liapunov-exponents
2001/11/07, 14:15, V5-148, Seminar Numerical Analysis
-
Thorsten Hüls: Heteroclinic orbits between nonhyperbolic fixed points
2001/10/24, 14:15, V5-148, Seminar Numerical Analysis
-
Sergey Pilyugin (St. Petersburg): New results on shadowing
2001/07/05, 12:30, V2-205, Seminar Numerical Analysis
|