Die 27 Geraden
Geraden im Raum
Wir beginnen mit folgenden Fragen:
- Gibt es 12 Geraden im Raum, sodass jede Gerade genau 5 der anderen Geraden
schneidet?
- Gibt es 27 Geraden im Raum, sodass jede Gerade genau 10 der anderen Geraden
schneidet?
- usw...
Viele derartige Fragen könnte man stellen, meist allerdings sollte die
Antwort "Nein" sein.
Die Schläfli'sche Doppelsechs
Dies ist die Lösung des 12-er Problems, sogar mit folgendem Zusatz:
Wir teilen die 12 Geraden in zwei Teilmengen,
sagen wir 6 rote und 6 blaue Geraden, und
- jede rote Gerade schneidet genau 5 blaue Geraden,
- jede blaue Gerade schneidet genau 5 rote Geraden!
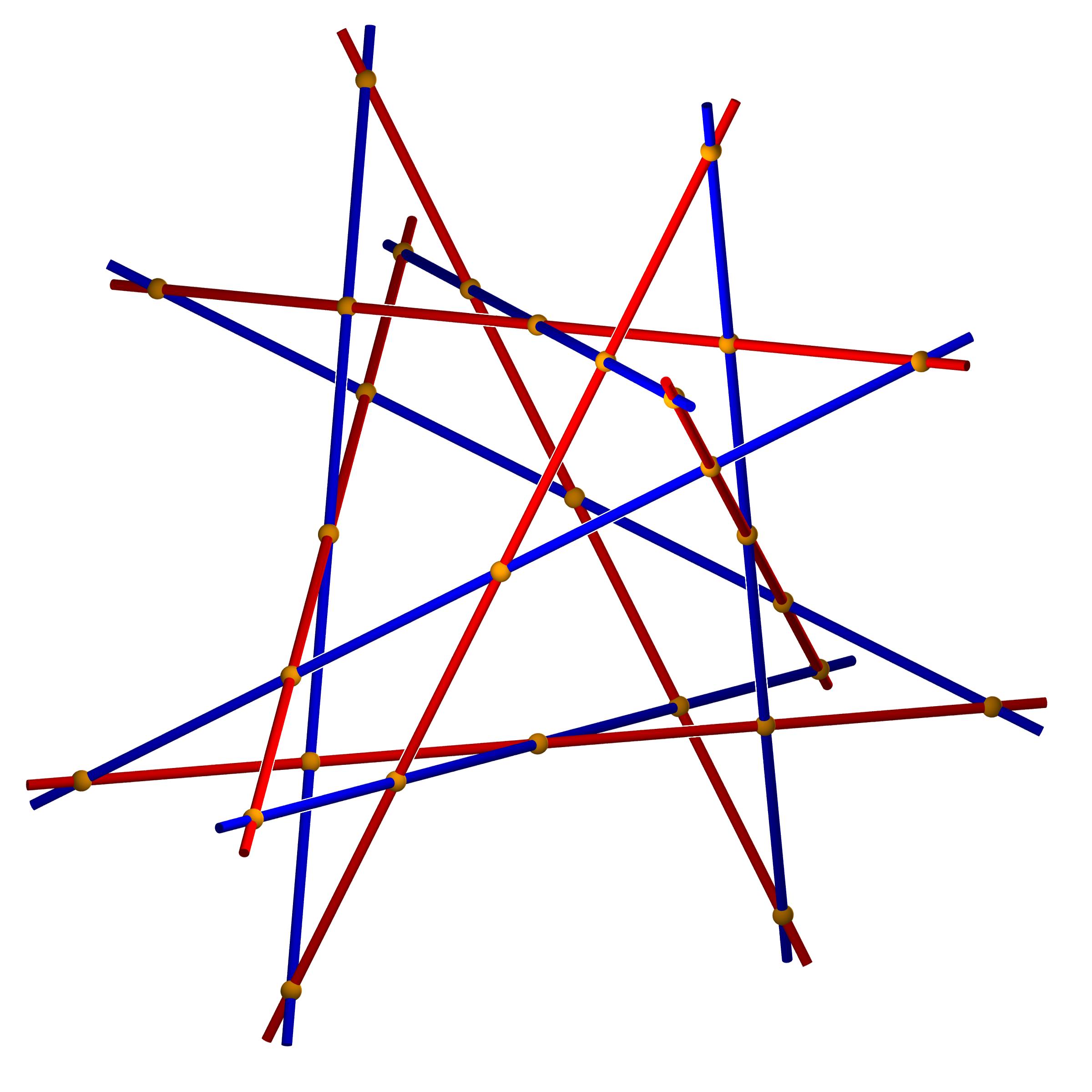
(Wiesinger)
Die Schläfli'sche Doppelsechs ist nach Ludwig Schläfli (1814-1895)
benannt, der diese Geraden-Konfiguration intensiv untersucht hat.
Die Konstruktion einer Schläfli'sche Doppelsechs ist ganz einfach, wenn
man den Trick kennt.
- Man beginnt mit einem Würfel (sagen wir mit Kantenlänge 1),
- man zeichnet vier der Ecken A, B, C, D aus, die zusammen ein Tetraeder erzeugen.
- Man viertelt die Würfel-Kanten und nimmt die Punkte, die den Abstand 1/4
von den Ecken A, B, C, D haben, dies liefert 12 Punkte auf dem Würfel.
- Verbindet man nun auf den 6 Würfel-Flächen jeweils gegenüberliegende
Punkte, so erhält man pro Würfel-Fläche 2
Geraden (man färbt eine Gerade blau und die andere
rot), insgesamt also
12 Geraden.
Bei der Farb-Wahl ist darauf zu achten, dass sich die roten Geraden nicht
schneiden sollen (dann schneiden sich auch die blauen nicht).
- Es ist leicht zu sehen, dass eine rote Gerade fünf der blauen Geraden
schneidet: rot-blaue Geradenpaare, die sich nicht schneiden, liegen auf
gegenüberliegenden Würfelflächen.
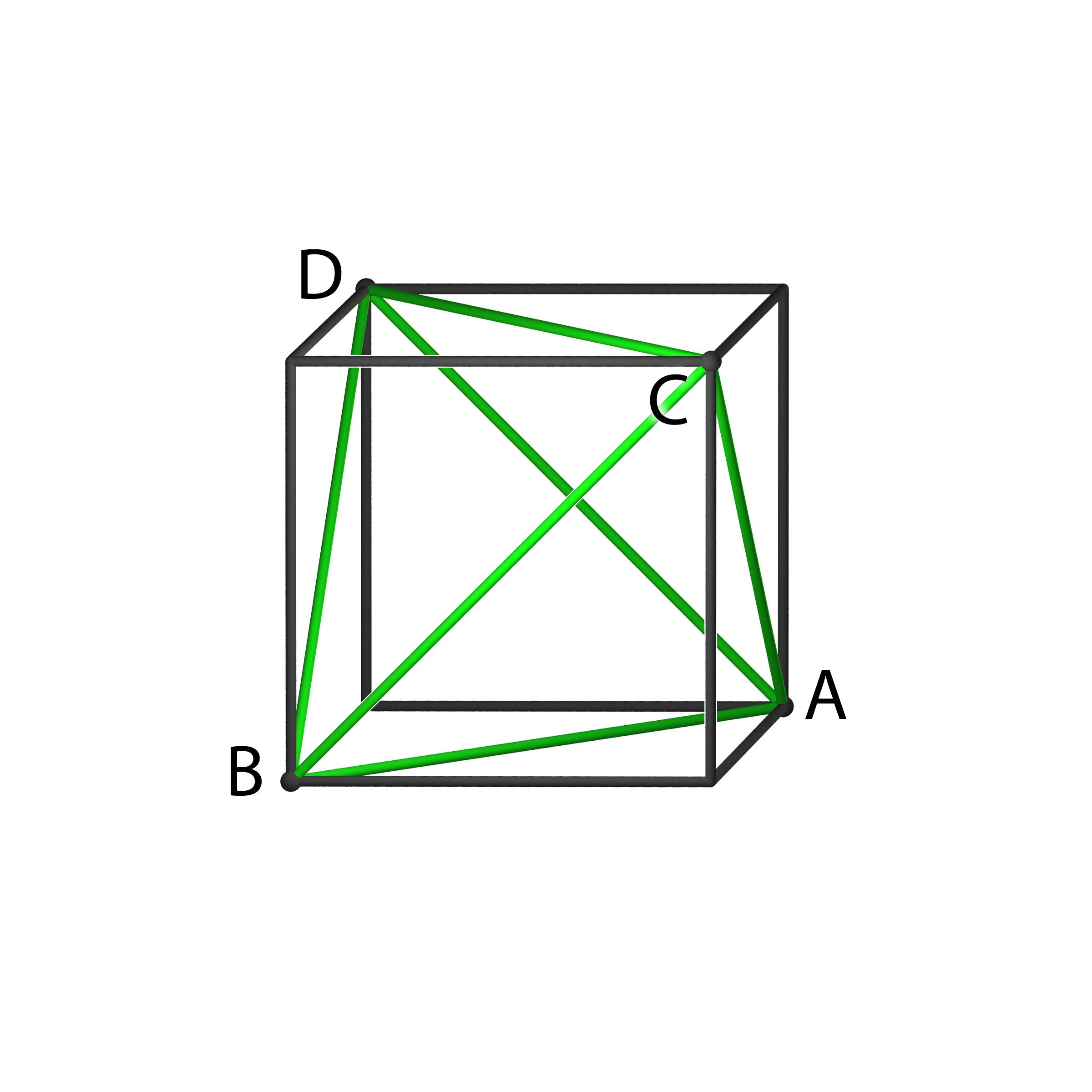
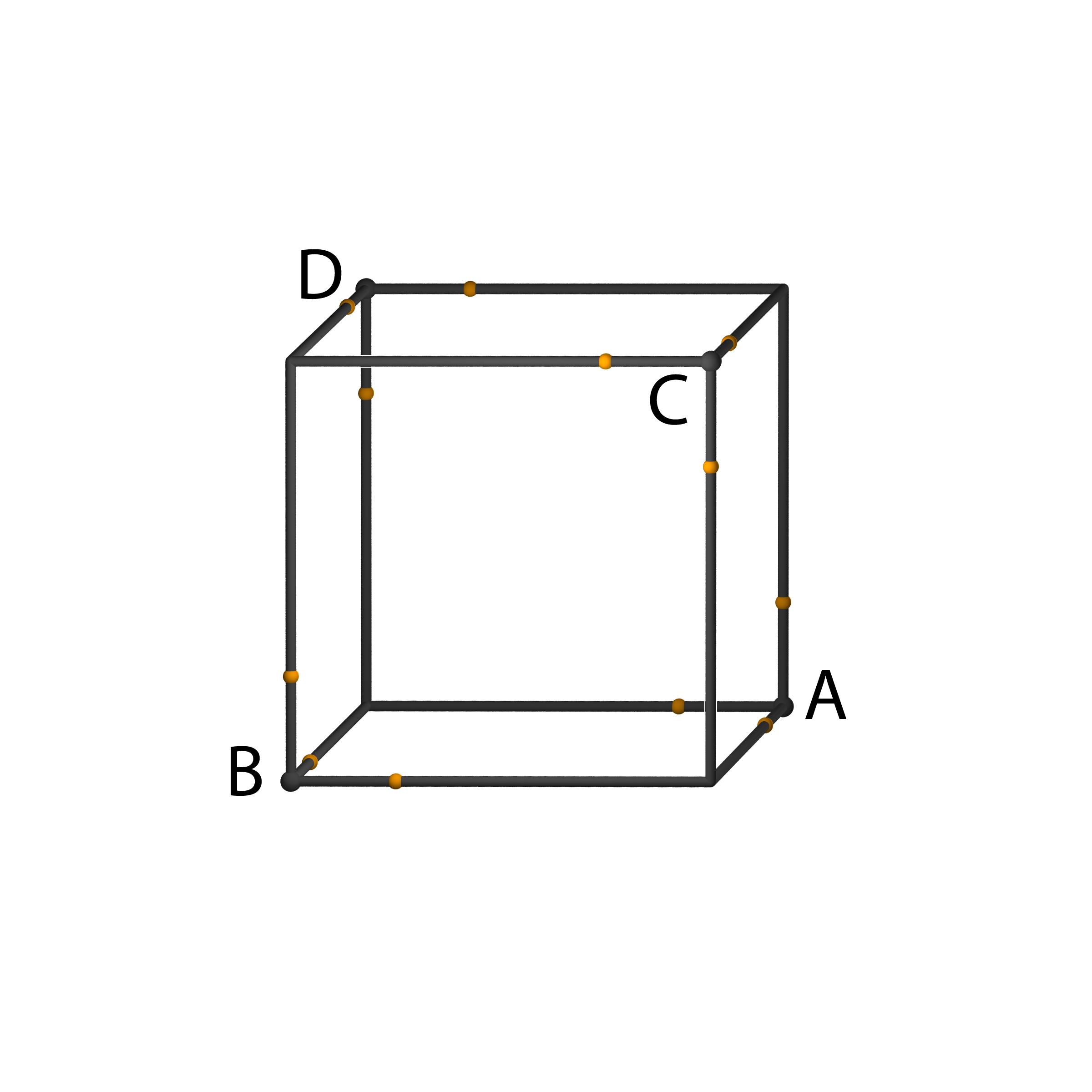
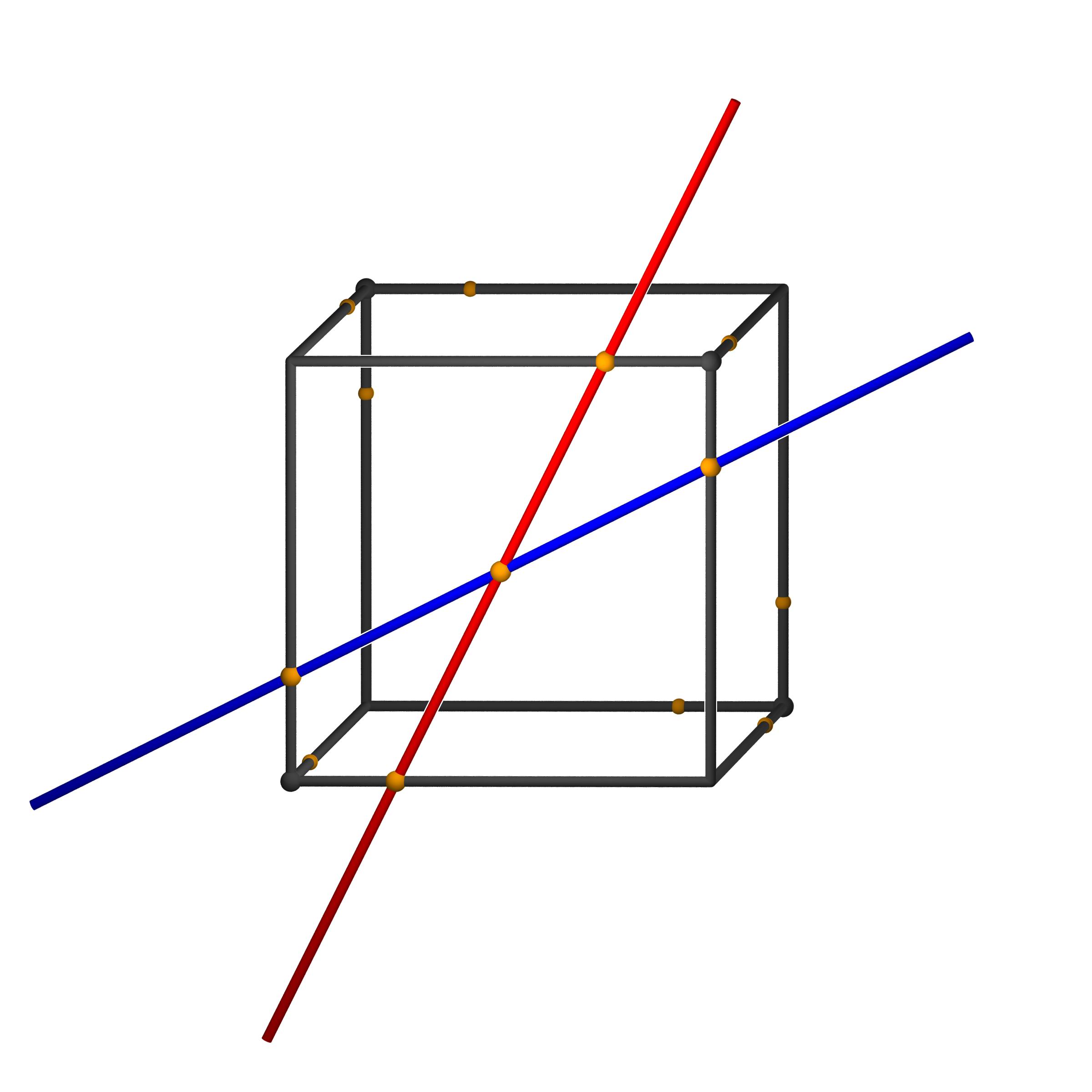
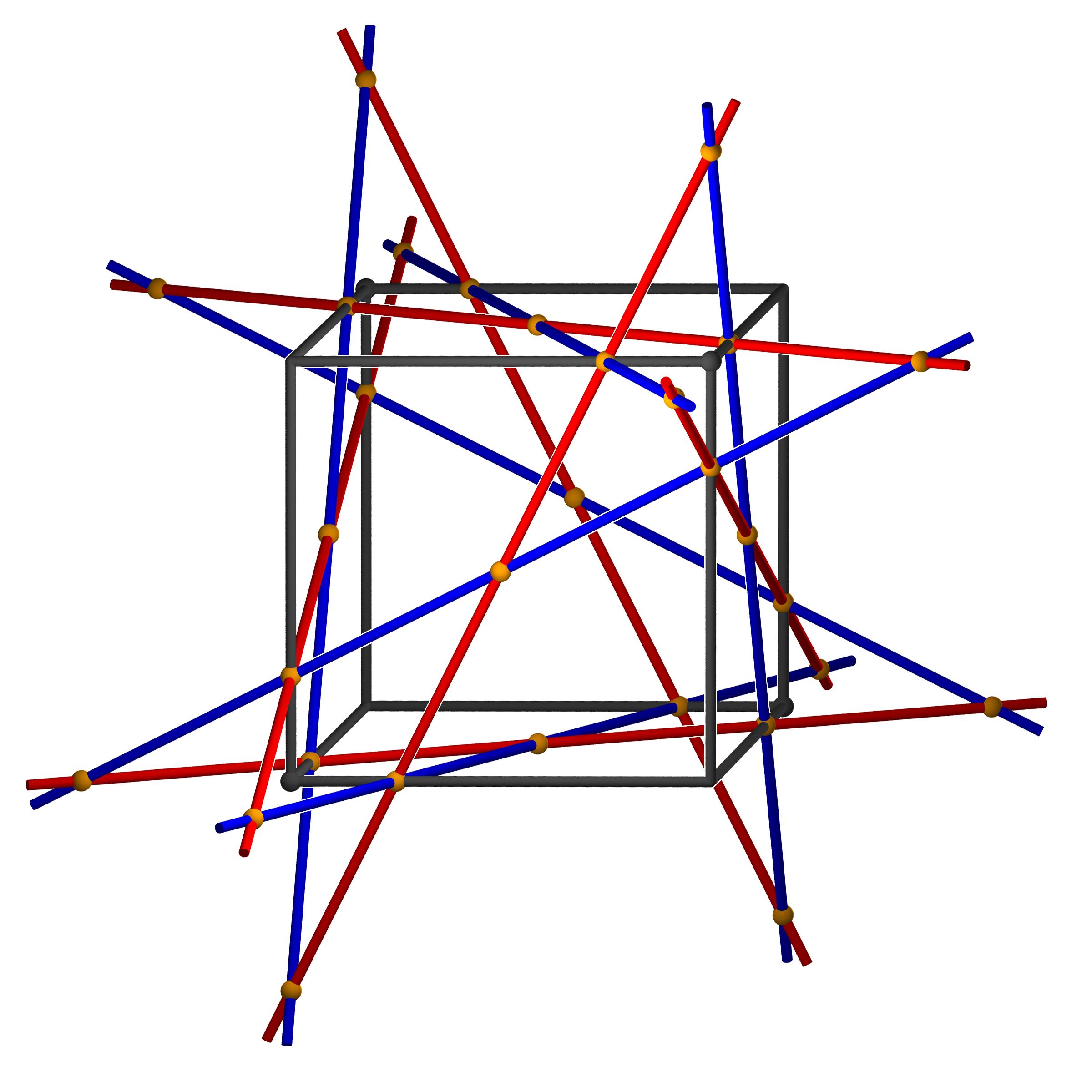
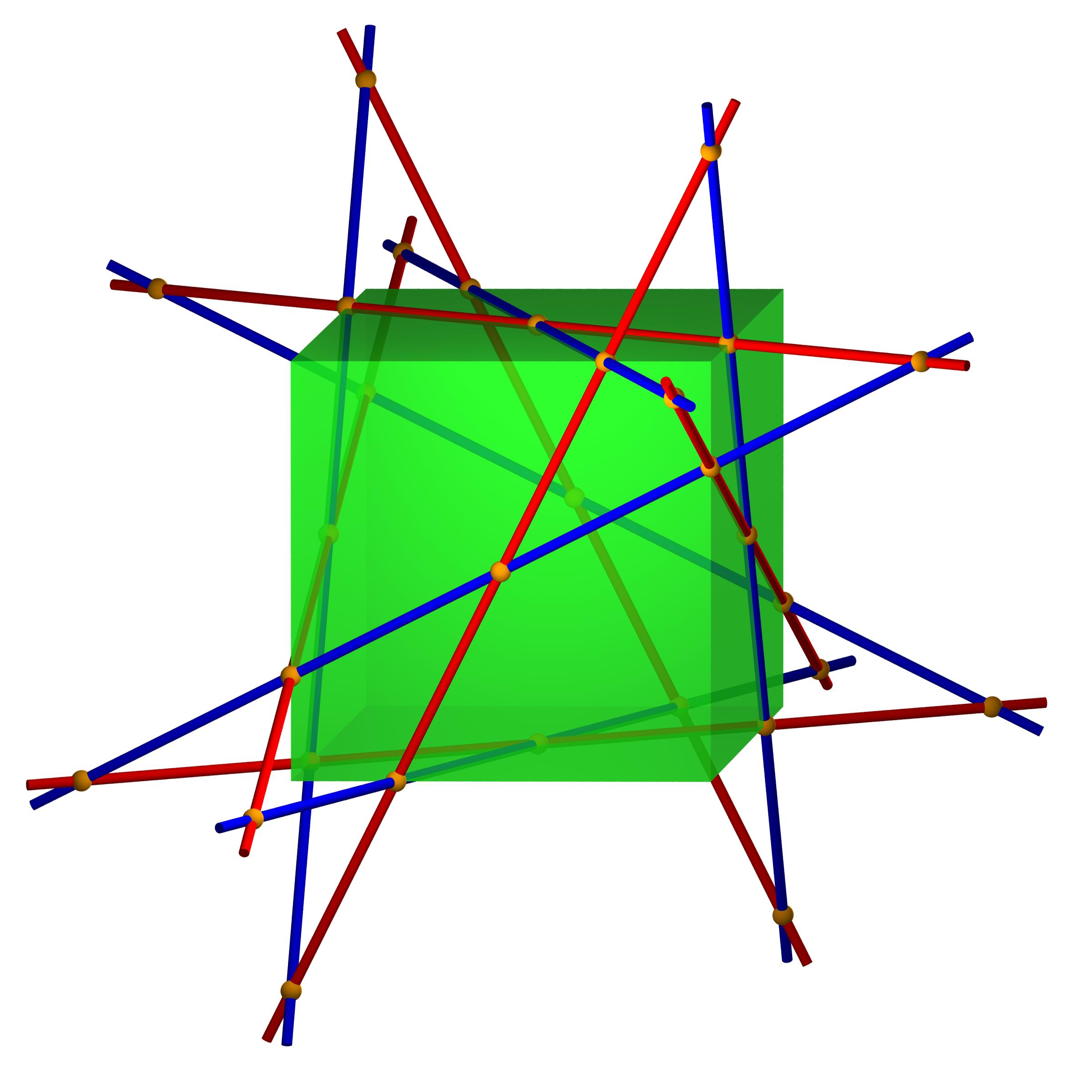
(Wiesinger)
Das 27-er Problem
Auch das 27-er Problem besitzt eine Lösung: die 27 Geraden auf einer
kubischen Fläche in allgemeiner Lage!

Flächen
Seit Descartes (1596-1650) werden viele geometrische Gebilde
durch algebraische Gleichungen beschrieben.
Die Methode hat den Nachteil, dass es schwierig werden kann, die
Gebilde zu visualisieren.
Flächen, also zweidimensionale Gebilde, werden dabei (oft) durch
algebraische Gleichungen in drei Variablen beschrieben.
Geraden auf Flächen:
Es gibt vollständig gekrümmte Flächen, bei denen jeder
Punkt zu einer Geraden gehört, die ganz in der Fläche liegt,
unendliche viele Geraden
enthalten, z.B. das einschalige Hyperboloid ("Kühlturm").
Insbesondere enthält eine derartige Fläche unendlich viele Geraden.
(Dies gilt für jede quadratische Fläche, sofern man
mit komplexen Koordinaten arbeitet!
Kubische Flächen
In einem Briefwechsel zwischen Arthur Cayley (1821-1895)
in Cambridge und George Salmon (1819-1904) in Dublin wurde zum ersten Mal notiert,
dass auf einer durch eine kubische Gleichung definierten glatten
Fläche immer genau 27 Geraden gibt. Publiziert wurde dies 1849.
Es gilt: Jede Gerade g schneidet genau 10 der übrigen, und zwar liegen
diese 10 Geraden in genau 5 "Dreier-Ebenen" (also in Ebenen,
die neben g noch genau zwei Geraden enthalten).
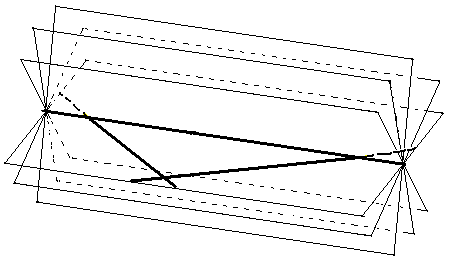
In jeder solchen Ebene gibt es also entweder ein Dreieck
aus Geraden, oder drei Geraden, die sich in einem Punkt schneiden.
Auf diese Weise erhält man also genau 45 Dreier-Ebenen.
| 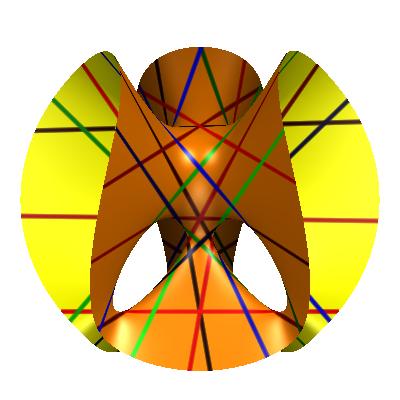
(Oliver Labs)
|
Beweise
In vielen Büchern zur algebraischen Geometrie finden sich die entsprechenden
Beweise.
- Van der Waerden: Einführung in die algebraische Geometrie
Springer Verlag 1939 (und 1973), 148-153.
- David Mumford: Algebraic Geometry I. Er schreibt in der Einleitung:
My goal is precisely to convey some of the classical geometric ideas
and to get "off the ground": in fact, to get to the
27 lines on the cubic - surely one of the gems hidden in the rag-bad of
projective geometry.
- M. Reid: Undergraduate Algebraic Geometry. LMS Student Texts 12
Cambridge University Press 1988.
- Klaus Hulek: Elementare algebraische Geometrie. (Vieweg studium, 2000).
Ausschnitt.
- Und viele andere Texte!
Beweisidee
-
Sei G die Menge der Geraden im P3, und C die Menge
der kubischen Flächen im P3, beides sind Varietäten.
Betrachte die Untermenge U aller Paare (g,F) in G×C
für die gilt: g liegt in F.
- Dimensionsbetrachtungen zeigen: Zu jedem F gibt es ein g mit (g,F) in U.
Also sehen wir: Jede kubische Fläche enthält mindestes eine Gerade.
-
Wir setzen voraus, dass F glatt ist (also in jedem
Punkt eine Tangentialebene besitzt).
- Fixiere eine Gerade g auf F.
Betrachte nun das Ebenen-Büschel aller Ebenen E, die g enthalten. Es ist
E∩F eine Kurve vom Grad 3, besser: die Vereinigung von g und einer Kurve vom Grad 2
(also einem Kegelschnitt).
- Man kann nun zeigen: Es gibt genau 5 Ebenen, in denen dieser Kegelschnitt zerfällt.
- Damit ist gezeigt: Die Gerade g schneidet genau 10 Geraden, die auf F liegen.
- Nun betrachten wir eine Dreier-Ebene E mit drei Geraden g1,
g3, g3.
Jede weitere Gerade schneidet diese Ebene in einem Punkt, der zu einer dieser
Geraden geh&aouml;rt, und auch nur zu einer dieser Geraden (hier verwendet man wieder die
Glattheit).
- Also erhalten wir zu jeder Geraden gi 8 weitere Geraden. Also
ingesamt 3×8 + 3.
Schläfli'sche Doppelsechsen auf einer kubischen Fläche
und das Wurzelsystem E6
Es gibt einen interessanten Zusammenhang zwischen dem 12-er und dem 27-er
Problem: Betrachtet man die 27 Geraden auf einer
kubischen Fläche in allgemeiner Lage, so gilt: es gibt
genau 36 Teilmengen dieser
27 Geraden, die eine Schläfli'sche Doppelsechs bilden!
Was ist die Bedeutung der Zahl 36 ? Dies ist die Anzahl der positiven Wurzel
des Wurzelsystems E6.
Wurzelsysteme
(4 Seiten, als Weiterklick-Sequenz; die Definition findet man auf der
letzten Seite. Das Wurzelsystem E6 ist an sich eine Teilmenge
des 6-dimensionalen (!) Raums.)
Freudenthal hat gezeigt, wie man in natürlicher Weise
eine explizite Bijektion zwischen den Teilmengen der 27 Geraden, die eine
Schläfli'sche Doppelsechs bilden
und den positiven Wurzel konstruieren kann.
Der Zusammenhang mit den 28 Doppeltangenten einer glatten ebenen Kurve vom Grad 4
Siehe: 27 + 1 = 28
Die Clebsche Diagonalfläche
1861 zeigte Clebsch dass man kubische Flächen
durch die sogenannte "pentahedrale" Normalform beschreiben kann
(dies war von Sylvester vermutet worden).
Die bisher existierenden Modelle
Literatur
- Cayley - Salmon: Briefwechsel
- Jakob Steiner: Crelle's Journal für Mathematik 53 (133-141),
Siehe auch: Steiner's Werke II, 651-659.
- Jordan: Oevres I, p.199-202, 203-206, 249-268)
- Felix Klein: Vorlesungen über
die Entwicklung der Mathematik im 19.Jahrhundert.
p.166-167
- David Hilbert, Stefan Cohn-Vossen: Anschauliche Geometrie.
- Die Schläfli'sche Doppelsechs (§ 25. p.146-151)
- Die 27 Geraden (p.145-146, 149-151)
- A. Henderson: The 27 lines upon the cubic surface, Cambridge, University Press, 1911.
- Oliver Labs,
The Cubic Surface Homepage (früher:
Algebraic Geometry Group,
University of Mainz, Germany).
Siehe auch Geraden auf Flächen
- Das
Literaturverzeichnis der Arbeit von Yamashita:
An elementary and purely synthetic proof for the double six theorem of
Schläfli.
Das geplante neue Modell
Beabsichtigt wird nun, ein Modell der Konfiguration dieser 27 Geraden allein (ohne
zugrundeliegende Fläche) anfertigen lassen.
Warum?
- Schon beim Vergleich der beiden Modelle einer Schläfli'schen
Doppelsechs (mit Würfel - ohne Würfel) stellt man fest, dass
der Würfel zwar hilft, die Konstruktion zu verstehen, dass er aber
ablenkt, wenn man sich nur auf die Geradenkonfiguration konzentrieren möchte
- Dies ist noch viel gravierender bei den bisher existierenden Modelle der
Cleb'schen Diagonalfläche: die jeweiligen Flächenkrümmungen
lenken die Aufmerksamkeit auf sich, zudem sind
viele Schnittpunkte, viele Geradenstücke verdeckt.
- Schon das Auffinden der 45 Dreiecke sollte in einem reinen Geradenmodell
viel einfacher sein!
- Es ist zu erwarten, dass ein reines Geradenmodell seinen eigenen Reiz
entfalten wird.
- Trotz des großen Interesses an dieser überraschenden
Geradenkonfiguration scheint es nirgendwo in der Welt bisher ein derartiges
Modell zu geben.
Ausführung
Die mathematischen
Vorarbeiten werden an der Fakultätat für
Mathematik vorgenommen:
- Wahl einer geeigneten Normalform, um einerseits
Mindestabstände und Schnittwinkel
zu optimieren,
andererseits aber um Symmetrien sichtbar zu machen.
- Angabe der Schnittpunkts-Koordinaten,
- der Abstände benachbarter Schnittpunkte auf den jeweiligen Geraden
- der geographischen Koordinaten für die Bohrungen der Kugeln
Prof. Dipl.-Ing. Friedhelm Kürpig (bisher Hochschule für bildende
Künste Hamburg) hat sich bereit erklärt, aufbauend auf diesen Vorarbeiten
ein derartiges Modell herzustellen:
- erst einen Prototyp aus einfacheren Materialien, Höhe etwa 120,
dann das eigentliche Modell
(dabei sollen zumindest beim Prototyp
die Geraden einer Schläfli'sche Doppelsechs
farbig herausgehoben werden);
- nur anhand des Prototypen kann abgeschätzt werden, welche Größe
das endgültige Modell haben kann.
Herr Kürpig hat vielfältige Erfahrungen zur Herstellung derartiger
Modelle; alle Kantenmodelle der Biellefelder Sammlung mathematischer Modelle
stammen von ihm (insbesondere das 120-Zell, von dem es weltweit nur ganz wenige
Modelle gibt, die alle von ihm stammen). Mit einer
Ausstellung
30 Jahre Konstruktive Geometrie an der HfbK wurde 2007
seine Arbeit an der Hochschule für bildende Künste Hamburg gewürdigt.
Planungsdaten (Beineke)
- Animation
- Die blauen und die roten Geraden bilden zusammen eine
Schläfli'sche Doppelsechs (mit 6 Schnittpunkten im Unendlichen).
- Man beachte, dass es drei hoizontale Ebenen gibt, in denen jeweils
3 schwarze Geraden liegen (unten und oben bilden sie ein Dreieck,
in der Mitte schneiden sich die drei Geraden in einem Punkt).
-
Blick von oben
-
Weitere Entwürfe
Last modified: Tue Sep 15 13:41:18 CET 2008











 Großansicht
Großansicht