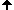 |
 |
 |
 |
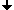 |
 |
| Summe | Faktorisierung | 3*Summe | 2*3*Summe | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 2 | 3 | |||
| 1+4 | 5 | 1 | 1 | 5 | 1 | 3 | 5 | 2 | 3 | 5 | |||
| 1+4+9 | 14 | 1 | 2 | 7 | 3 | 2 | 7 | 3 | 4 | 7 | |||
| 1+4+9+16 | 30 | 2 | 5 | 3 | 2 | 5 | 9 | usw | |||||
| 1+4+9+16+25 | 55 | 5 | 1 | 11 | 5 | 3 | 11 | ||||||
| 1+4+9+16+25+36 | 91 | 1 | 7 | 13 | 3 | 7 | 13 | ||||||
| 1+4+9+16+25+36+49 | 140 | 7 | 4 | 5 | 7 | 4 | 15 | ||||||
| 1+4+9+16+25+36+49+64 | 204 | 4 | 3 | 17 | 4 | 9 | 17 | ||||||
| 1+4+9+16+25+36+49+64+81 | 285 | 3 | 5 | 19 | 9 | 5 | 19 | ||||||
| 1+4+9+16+25+36+49+64+81+100 | 385 | 5 | 11 | 7 | 5 | 11 | 21 | ||||||
| 1+4+9+16+25+36+49+64+81+100+121 | 506 | 11 | 2 | 23 | 11 | 6 | 23 | ||||||
| 1+4+9+16+25+36+49+64+81+100+121+144 | 650 | 2 | 13 | 25 | 6 | 13 | 25 | ||||||
| 1+4+9+16+25+36+49+64+81+100+121+144+169 | 819 | 13 | 7 | 9 | 13 | 7 | 27 | ||||||
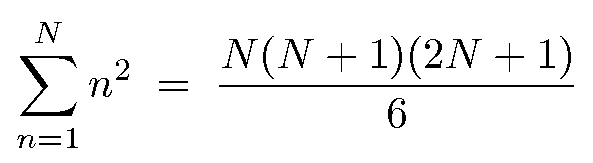
Beweise:
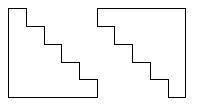
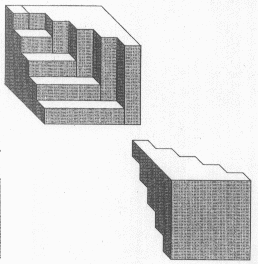
Man baue 6 Pyramiden der folgenden Form (hier für N=4):
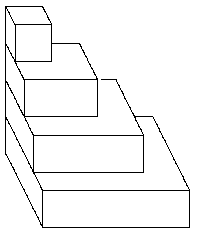
Sie lassen sich zu einem Quader mit den Kantenlängen N, N+1, 2N+1 zusammensetzen.
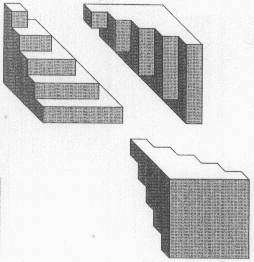
Hier das Zusammensetzen von drei derartigen Pyramiden:
 |  | |
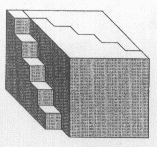 |
Man erhält einen Quader "mit einer Außentreppe".
Offensichtlich bilden zwei solche Quader mit ihren Außentreppen
zusammen einen kompakten Quader!
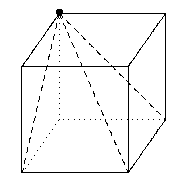
Im Chinesischen heißen diese Pyramiden Yang-ma, sie spielen eine wichtige Rolle zum Beispiel bei der Berechnung des Volumens von Pyramiden-Stümpfen (Liu Hui, 3.Jh.u.Z., Kommentar zu den 9 Kapiteln).
Die obigen Pyramiden, die wir beim Beweis der Formel für die Summe der ersten N Quadratzahlen verwendet haben, verallgemeinern den geometrischen Beweis für die Summe der ersten N Zahlen.
Hier der Fall N=5: