DynaGeo für Topologen

Wir wollen zeigen, wie man dynamische Geometrie-Software wie zum Beispiel "DynaGeo" (früher nannte es sich "Euklid") verwenden kann, um topologische Fragestellungen anzugehen.

Als erstes zeigen wir:

Der Rand eines Möbius-Bands ist unverknotet

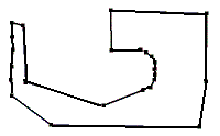
Wir beginnen mit folgendem Kantenzug, der offensichtlich als Rand eines typischen Möbius-Bands interpretiert werden kann:

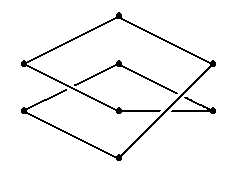
Rot markiert sind jeweils die Ecken, die bewegt worden sind:


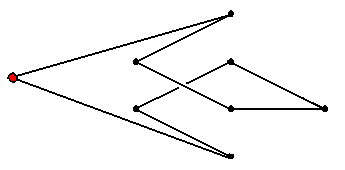
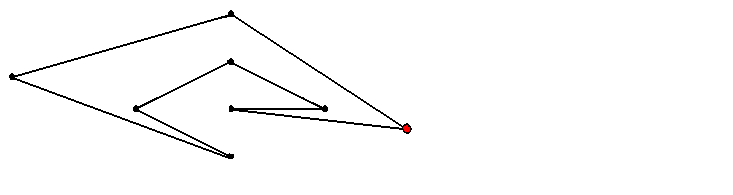
Beide Abänderungen lassen sich recht mühelos durch topologische Äquivalenzen des R3 realisieren! Und das Ergebnis ist offensichtlich unverknotet!

Noch eine Entknotung:

Wir betrachten den Knoten, den wir als ein durchaus nicht-triviales Beispiel vorgestellt hatten:

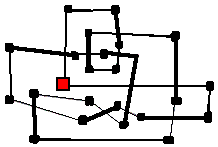
Bei Überkreuzungen ist jeweils eine der beiden Kanten fett gezeichnet: sie verläuft vor der dünn gezeichneten Kante. Insgesamt gibt es hier 9 Überkreuzungen.

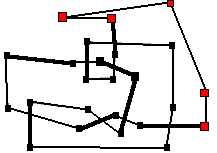
Wir wollen zeigen, dass dieser Knoten unverknotet ist! In den hier gezeigten Bildern sind jeweils diejenigen Ecken rot markiert, die bewegt werden sollen.
Im obigen Bild ist nur eine Ecke rot: sie ist durch zwei dünne Kanten verbunden, die beide zu Überkreuzungen gehören: bewegen wir diese Ecke nach oben rechts, so entfernen wir zwei Überkreuzungen!

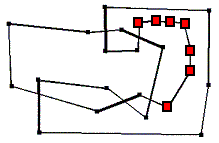
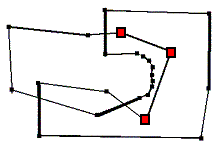
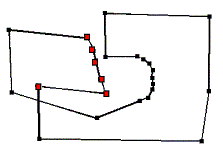
Bisher haben wir in jedem Schritt zwei Überkreuzungen beseitigt, im letzten Schritt wird noch die letzte Überkreuzung entfernt:

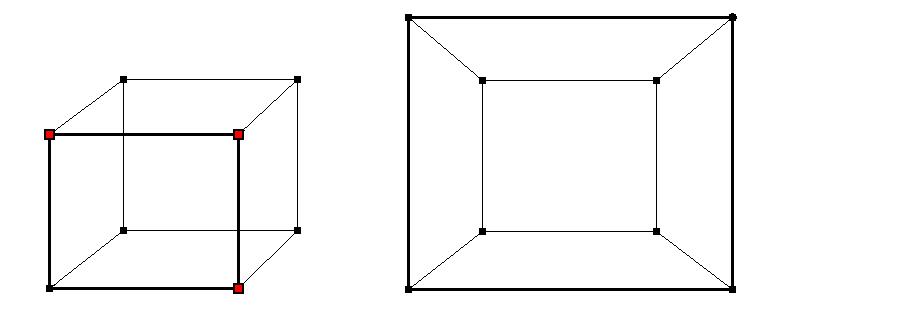
Netze: Zum Beispiel das eines Würfel

Das Verschieben von Ecken mit Hilfe von DynaGeo kann man auch sehr gut verwenden, um Netze von Körpern miteinander zu vergleichen.

Als erstes betrachten wir die typische Ansicht eines Würfels in Parallel-Projektion. Hierbei treten zwei Überkreuzungen auf. Durch das Bewegen dreier Ecken beseitigen wir diese Überkreuzungen und erhalten ein Bild, das auch durch Zentralprojektion entsteht:

Das Oktahemioktaeder als Torus

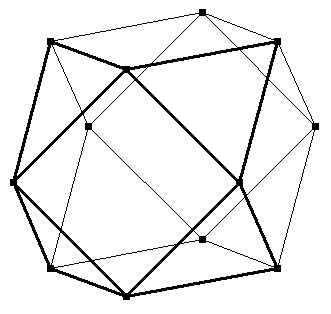
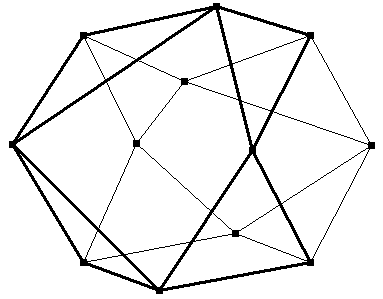
Um das Oktahemioktaeder als Torus zu sehen, bewegen wir zuerst die Ecken in der mittleren horizontalen Ebene: die beiden vorderen nach links und weiter nach hinten, die beiden hinteren nach rechts und etwas nach vorne.

nun wird noch die Lage der beiden oberen Ecken vorne und hinten vertauscht:

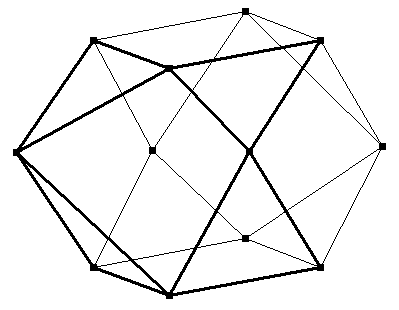
Hier das Ergebnis:

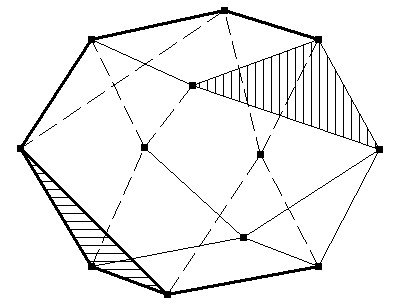
Das gleiche Bild, nun aber sind die verdeckten Kanten gestrichelt:

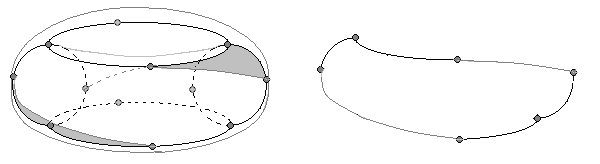
Hier ein entsprechender "runder" Torus, mit den 12 Ecken und einigen der Kanten; wie oben sind auch hier zwei der Dreiecke markiert - rechts daneben eines der Sechsecke:

Was ist Topologie?

Topologen betrachten Invarianten topologische Räume unter stetigen Deformationen. Es gibt ganz wilde Konstruktionen topologischer Räume - aber die sind gar so sehr von Interesse: vor allem interessiert man sich für Polyeder, also für Räume, die eine simpliziale Struktur haben: sie sind aus ganz einfachen Räumen wie Kanten, Dreiecken, Tetraedern usw zusammengesetzt. Allerdings gilt: Polyeder bis auf topologische Äquivalenz zu klassifizieren, ist ein völlig unlösbares Problem!

Und man kann zeigen, dass es genügt, Deformationen zu betrachten, die lokal durch affine Transformationen beschrieben werden, also PL-Topologie zu betreiben (PL steht für "piecewise linear", also für "stückweise linear"). Das sind aber Operationen, die man (in niedrig-dimensionalen Beispielen) durch dynamische Geometrie-Software sehr gut veranschaulichen kann!