Flächen
(Kompakte, geschlossene, triangulierbare Flächen)
Klassifikation
Jede solche Fläche ensteht aus der 2-Sphäre durch Anheftung von "Henkeln" und "Kreuzhauben"
(und das Anheften einer Kreuzhaube und eines Henkels liefert das Gleiche wie das Anheften dreier Kreuzhauben).
Es gibt also folgende Liste:
- Ft (mit t ≥ 0) ensteht aus
der 2-Sphäre durch Anheftung von t Henkeln.
- Nt (mit t ≥ 1) ensteht aus
der 2-Sphäre durch Anheftung von t Kreuzhauben.
|
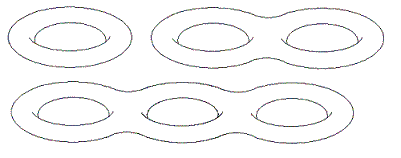
Die Flächen F1, F2 und F3:
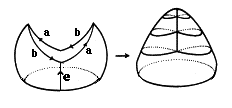
Das Anheften eines Henkels:

Das Bilden einer "Kreuzhaube"
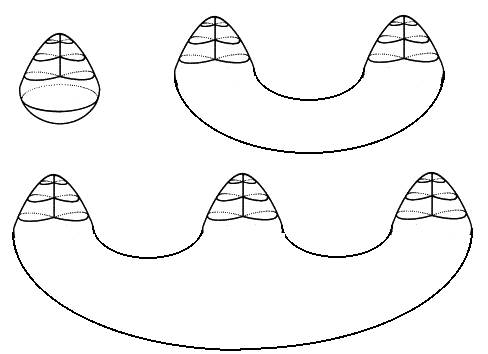
Die Flächen N1, N2 und N3:
Euler-Charakteristik der FLäche F
| e | Anzahl der Ecken
|
| k | Anzahl der Kanten
|
| f | Anzahl der Polygone
|
Es ist
Beispiel: die 2-Sphäre
Hier die Werte von χ(Ft) und χ(Nt):
Also: Kennt man die Euler-Charakteristik χ(F), so gilt:
- Ist χ(F) ungerade, so ist F eindeutig bestimmt: F = N2-χ(F).
- Ist χ(F) gerade, etwa χ(F) = 2n, so ist F entweder gleich
F1-n und gleich N2-2n).
Wie unterscheidet man diese beiden Fälle? Man prüft:
- ist in F ein Möbiusband einbettbar, so ist F = N2-2n
- ist in F kein Möbiusband einbettbar, so ist F = F1-n.



