by Markus Rost (Notes, July 2022, 19 pages)
We formulate and prove a certain relation in the automorphism group of H⊗H for an involutive Hopf algebra H (S2=1). It lifts the standard cubic relation in the automorphism group of a free group of rank 2.
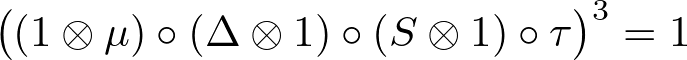
More generally, the braid group B4 acts on H⊗H for any Hopf algebra H.
We pose also the question for the universal relations which hold for commutative Hopf algebras and for cocommutative Hopf algebras.
The main purpose of the current text is to require advice on the current status of the topic.
Full text (August 2, 2022): [pdf]
by Markus Rost (Notes, September 2022, 15 pages)
For vector bundles V over a ring (in particular with 2 not invertible) a family of modules M(V) is defined. Each M(V) is associated to a finite group scheme G of order 2. The constant group scheme Z/2Z yields the module of quadratic forms, the group scheme μ2 the module of symmetric bilinear forms.
Currently the text has two parts.
The second (older) part contains an introduction which explains the basic idea in detail. The relation with group schemes of order 2 is indicated. Moreover for the rank 2 case there is a formula for the Dickson invariant for symmetries of a non-degenerate "form" in M(V). It takes values in the corresponding group scheme.
The first (newer) part one gives a somewhat different definition of the modules with other notations. The half-determinant is defined. The method used for the half-determinant might be also interesting for the classical case of odd-dimensional quadratic forms. No group schemes in this part yet.
Full text (September 27, 2022): [pdf]