Funktionen in zwei Variablen
Wir betrachten zum Beispiel die Funktion F(x,y) = x*y, dabei sei
-5 ≤ x ≤ 5 und -10 ≤ y ≤ 10.
Wertetabelle
Als erstes legen wir eine Wertetabelle an, und zwar für alle
ganzzahligen Werte x und y in den genannten Grenzen. Hier das Ergebnis
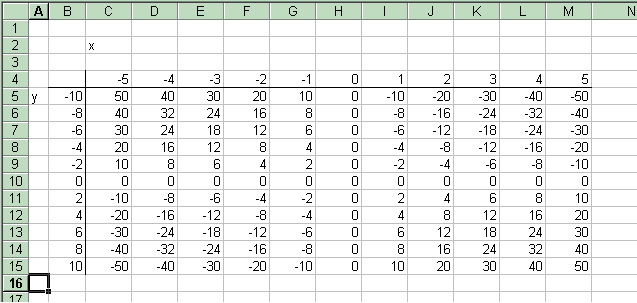
dabei steht zum Beispiel in der Zelle C5 der Wert
F(x,y) für x = -5 und y = -10, also F(-5,-10) = (-5)*(-10) = 50;
daneben in D5 steht F(-4,-10) = (-4)*(-10) = 40, usw.
Die Schritte, um diese Wertetabelle zu erhalten, sind ganz einfach:
- x-Werte:
Als erstes trage man -5 in die Zelle C4 und -4 in die Zelle D4 ein,
markiere beide Zellen, gehe mit dem Cursor in die rechte untere Ecke dieses
Bereichs und ziehe mit gedrückter Maustaste nach rechts ...
- y-Werte: Entsprechend tragen wir -10 in die Zelle B5 und -8 in die Zelle B6
ein, markieren diesen Bereich und ziehen ihn nach unten ...
- Die Formel. In die Zelle C5 wird = C$4*$B5 eingetragen: dies
ist eine Formel
(man sieht dies am Gleichheitszeichen) und zwar zur Multiplikation zweier
Zahlen, nämlich von C$4 und $B5. Dabei ist für den ersten Faktor C$4 die Zeile fixiert, nämlich die mit Nummer 4
(denn es steht
hier $4, eine absolute Adressierung), der Spaltenverweis C steht für gleiche
Spalte (relative Adressierung), beim zweiten Faktor
$B5 ist die Spalte
B fixiert (absolute Adressierung), dagegen steht die 5 für die gleiche Zeile
(also relative Adressierung).
- Kopieren der Formel.
Nun ist die Formel nur noch in die weiteren Zellen zu kopieren: Markiere die Zelle C5,
ziehe nach unten bis zur Zelle C15, ziehe nach rechs bis zur Zelle M15. Fertig!
Vorher hatten wir allerdings noch die Spaltenbreiten der
Spalten A bis M verkleinert! und den Buchstaben x in die Zelle C2, den Buchstaben y
in die Zelle A5 eingetragen (auf diese Weise weiß man, welches die x-Werte,
und welches die y-Werte sind). Außerdem wurden noch zwei Linien gezogen, eine rechts
von der B-Spalte, die andere unter der Zeile mit Nummer 4. Dies dient der
Klarheit, ist aber nicht notwendig.
Wir haben auf diese Weise die gesuchte Wertetabelle erhalten.
Der Funktionsgraph als Fläche
Nun wollen wir eine graphische Darstellung erhalten.
Der Bereich B4..M15 wird markiert und es wird Einfügen -
Diagramm aufgerufen. Unter Standard-Typen wählt man
Oberfläche und da
den ersten Untertyp, also 
Dann Weiter, Weiter, Weiter, Ende.
Was man erhält, sieht
folgendermaßen aus:
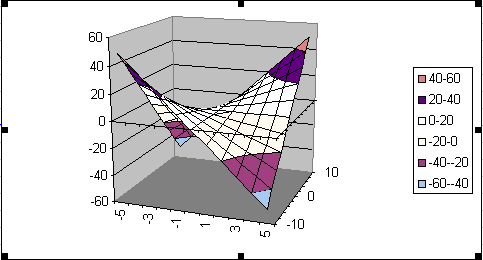
Eine Erläuterung, wie dieses Bild zu interpretieren ist, findet man
auf der Seite Excel-3.
Änderung der Ansicht:
Nun kommt aber das Beste: Diese Fläche kann man sich von allen möglichen Seiten
aus ansehen, genauer: offensichtlich befindet sie sich innerhalb eines Quaders, und man kann
nun diesen Quader beliebig drehen. Dazu klicke man auf eine der Ecken, und halte die linke
Maustaste gedrückt, während man die Maus bewegt. Man sieht dann nur noch
den Quader, zum Beispiel die linke Ansicht
(durch ein kleines Quadrat ist die Ecke markiert,
die angeklickt wurde);
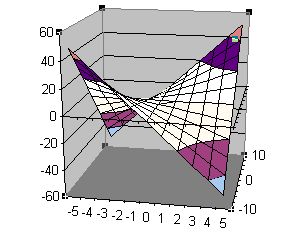
sobald man die Maustaste losläßt, erscheint dann das rechte Bild:
| 
|
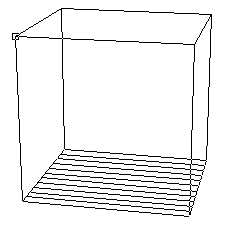
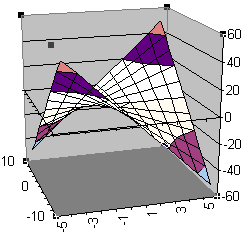
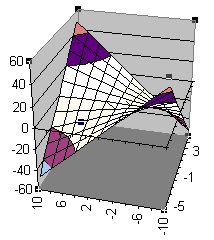
Hier zwei weitere Ansichten der Fläche, die man durch Drehen des Quaders erhält:
Man muss sich konzentrieren, um die Bilder jeweils als
perspektivische Ansichten wahrzunehmen; es wurde jeweils um die z-Achse
(entgegen dem Uhrzeigersinn) gedreht; zusätzlich wurde leicht nach vorne gekippt...
Bemerkungen:
- Durch die Farbgebung der Fläche sind
Höhenlinien markiert;
man kann sich auch direkt ein
Höhenlinienbild zeichnen lassen!
-
Man beachte, dass wir den Bereich B4..M15 und nicht etwa nur C5..M15 markiert haben:
Die Randspalte B und die Randzeile 4 werden von Excel zur Beschriftung der x-Achse
(im ersten Bild schräg nach unten links) und der y-Achse (nach rechts) verwandt.
Wichtig ist dabei, dass die Zelle B4 leer war.
- So schön diese Möglichkeit zur Visualisierung von
Funktionen ist, so ist sie doch sehr umständlich (da man zuerst
eine Wertetabelle produzieren muss). Einfacher geht es, wenn man statt
Excel eines der Mathematik-Pakete wie
Maple, Mupad oder Mathematica verwendet: dort erhält man
ganz entsprechende Bilder (wahrscheinlich sogar genauer gezeichnet), und
zwar mit ganz einfachen Befehlen.
Als Beispiel: Eingabe und Ausgabe bei Maple.
Excel ist eben nicht für mathematische Anwendungen
konzipiert, sondern zur Auswertung gegebener Daten, also zum Beispiel
zur Auswertung von Daten, die in Abhängigkeit von zwei Parametern
gewonnen wurden. Und dabei wird ja eine Tabelle ähnlich unserer Werte-Tabelle entstehen, die dann (wie dargestellt) visualisiert werden
kann!
- Festgehalten sollte aber folgendes werden: Der Bereich C5..M15 ist
eine Matrix (ein rechteckiges Zahlenfeld), und Excel liefert
für jede Matrix ein derartiges Oberflächenbild.
Höhenlinienbild
Um ein reines Höhenlinienbild (wie man es aus dem Atlas oder von Wanderkarten
her kennt) zu erhalten,
muss man nach der Wahl Einfügen -
Diagramm - Oberfläche den (dritten)
Untertyp 
auswählen. Man erhält dann folgendes Bild:
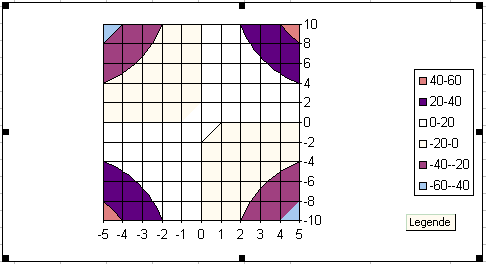
Eine Erläuterung, wie dieses Bild zu interpretieren ist, findet man
auf der Seite Excel-3.
