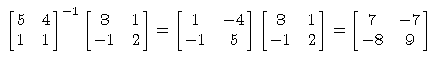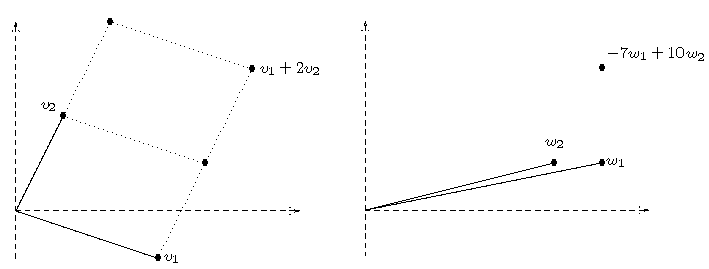Basen endlich erzeugter Vektorräume
Sei K ein Körper.
Vorausgesetzt werden die
Definitionen: Vektorraum,
(Die Elemente eines Vektorraums nennt man oft einfach
"Vektoren".)
Unterraum, Summe zweier Unterräume.
Linearkombination.
(Dabei handelt es sich jeweils um endliche
Linearkombinationen: auch wenn wir über eine unendliche Indexmenge
summieren, setzen wir voraus, dass nur endlich viele Summanden von Null
verschieden sind.)
Sei V ein K-Vektorraum.
Bezeichnung: Ist {vi | i in I} eine Teilmenge von V, so schreibt man
< vi | i in I >
für die Menge aller Linearkombinationen
der Vektoren vi.
|
Es gilt: < vi | i in I > ist der kleinste
Untervektorraum
von V, der die Vektoren vi enthält.
|
(d.h.: Erstens, < vi | i in I > ist ein Untervektorraum von V.
Und zweitens,
ist U ein Untervektorraum von V, der alle vi (i in I)
enthält,
so ist < vi | i in I> in U enthalten.)
Grundbegriffe
- Erzeugendensystem.
Ist V = < vi | i in I >, so sagt man, dass die Menge
{ vi | i in I } den Vektorraum erzeugt, und man nennt
{ vi | i in I } ein Erzeugendensystem.
Besitzt V ein endliches Erzeugendensystem, so sagt man, dass V ein
endlich erzeugter Vektorraum ist.
-
Lineare Unabhängigkeit.
Eine Teilmenge { vi | i in I } von V mit paarweise verschiedenen
Elementen vi heißt linear unabhängig, wenn eine
Linearkombination Σi in I λi vi
nur dann gleich Null ist, wenn für alle Koeffizienten λi = 0
gilt.
- Basis.
Man nennt { vi | i in I } eine Basis von V, falls
{ vi | i in I } ein linear unabhängiges Erzeugendensystem ist.
Ist I endlich, so verlangt man manchmal zusätzlich, dass die Menge I
geordnet ist, etwa I = {1,2,...,n}. Zur Unterscheidung sollte man dann von
einer geordneten Basis sprechen.
|
Beispiel. Im Kn bilden die Vektoren ei =
[0,...,0,1,0,...,0] mit 1 ≤ i ≤ n eine Basis, man nennt dies
die Standard-Basis (dabei ist der i-te Koeffizient von ei
gleich 1, alle anderen Koeffizienten sind 0):
- die Vektoren e1,...,en bilden ein
Erzeugendensystem, denn sind a1,...,an Elemente aus K,
so ist
[a1,...,an] = Σ
aiei
- Die Vektoren e1,...,en sind linear unabhängig, denn sind λ1,...,λn Elemente aus K,
mit Σi λiei = 0, so ist also
[λ1,...,λn] der Nullvektor, also sind alle
Koeffizienten λi = 0.
Die Bedeutung von Basen
Sei B eine Basis des Vektorraums V. Wir beschränken uns
hier auf den Fall einer endlichen Basis.
Sei etwa
B = {v1,...,bn}.
|
Folgerung:
Charakterisierung von Basen:
Sei V ein Vektorraum. Sei B eine Teilmenge von V.
Die folgenden Aussagen sind äquivalent:
- B ist eine Basis.
- B ist ein minimales Erzeugendensystem.
(d.h.: B ist ein Erzeugendensystem, und keine echte
Teilmenge von B ist ein Erzeugendensystem.)
- B ist eine maximale linear unabhängige Teilmenge.
(d.h.: B ist eine
linear unabhängige Teilmenge, und keine echte
Obermenge von B in V ist eine linear unabhängige Teilmenge.)
|
Beweis: (1) impliziert (2): Sei also B eine Basis.
Zu zeigen ist, dass echte Teilmengen von B keine Erzeugendensysteme
sind: verwende die Implikation "(1) impliziert (2)" des Lemmas.
(1) impliziert (3). Wieder sei B eine Basis.
Zu zeigen ist, dass echte Obermengen von B nicht linear unabhängig
sein könen. Auch hier verwende die Implikation "(1) impliziert (2)" des Lemmas.
(2) impliziert (1): Sei nun E ein minimales Erzeugendensystem.
Zu zeigen ist: E ist linear unabhängig. Gäbe es eine
nicht-triviale Linearkombination
Σ λivi = 0
mit paarweise verschiedenen vi in E, und ist etwa
λs ≠ 0, so ist vs Linearkombination der
übrigen Elemente von E, und demnach ist E-{vs}
ein Erzeugendensystem - Gegensatz zur Minimalität von E.
(3) impliziert (1). Sei S maximale linear unabhängige Teilmenge.
Zu zeigen ist: jedes Element v aus V ist Linearkombination der Elemente
aus S. Wäre v nicht in < S >, so liefert die Implikation
"(2) impliziert (1)" des Lemmas einen Widerspruch.
|
Ergänzungssatz:
Sei V ein Vektorraum. Sei E ein endliches Erzeugendensystem von V,
sei S eine linear unabhängige Teilmenge von V.
Dann gibt es eine
Untermenge E' von E, so dass die Vereinigungsmenge von S
und E' eine Basis von V ist (und S und E' disjunkt sind).
|
Beweis: Sei E = {w1,...,wm}.
Für 0 ≤ i ≤ m sei
Vi = S + < w1,...,wi >.
Sei E' die Menge aller wi, die nicht zu Vi-1
gehören.
Mit Induktion zeigt man: die Vektoren in S
bilden zusammen mit den Vektoren in {w1,...,wi}, die
zu E' gehören, eine Basis Bi
von Vi.
Für i = 0 ist nicht zu zeigen.
Sei nun i > 0. Ist Vi-1 = Vi, so ist die konstruierte
Basis Bi-1 von Vi-1 die gesuchte Basis
Bi von Vi.
Sei nun Vi-1 ein echter Unterraum von Vi. Es ist
Vi = Vi-1 + < wi > und wi
gehört zu E'.
Da Bi-1 eine Basis von Vi-1 ist, ist
Bi-1∪{wi} ein Erzeugendensystem für
Vi.
Da wi nicht zu < Bi-1 > = Vi-1
gehört, ist die Menge
Bi-1∪{wi} linear unabhängig (nach dem
Lemma). Dies zeigt, dass Bi =
Bi-1∪{wi} eine Basis von
Vi ist.
Folgerungen.
Sei V ein endlich erzeugter Vektorraum.
- Jede linear unabhängige Menge von V
kann zu einer Basis erweitert werden.
- (Basisauswahlsatz) Jedes endliche Erzeugendensystem von V besitzt eine
Teilmenge, die eine Basis ist.
|
|
Insbesondere gilt: Jeder endlich erzeugte Vektorraum besitzt eine
endliche Basis.
|
Beweis: Die erste Aussage
ist nur eine Abschwächung des Ergänzungssatzes.
(In 1 steht zusätzlich, dass man S durch Elemente
eines vorgegebenen Erzeugendensystems zu einer Basis erweitern
kann.)
Die zweite Aussage ist ein Spezialfall des Ergänzungssatzes:
nimm für S die leere Menge.
Die Bedeutung der Existenz einer Basis
Da jeder endlich erzeugte Vektorraum eine Basis besitzt, gilt:
- Jeder endlich erzeugte Vektorraum lässt sich koordinatisieren.
- Jeder endlich erzeugte Vektorraum ist zu einem Standard-Vektorraum
isomorph.
|
Wichtige Folgerung:
Sei V ein Vektorraum. Sei E ein endliches Erzeugendensystem von V,
sei S eine linear unabhängige Teilmenge von V.
Dann ist |S| ≤ |E|.
Insbesondere gilt: Je zwei Basen eines endlich erzeugten Vektorraums haben
gleiche Kardinalität.
|
Beweis: Induktion nach der Anzahl s der Elemente von V von S, die
nicht zu E gehören.
Ist s = 0, so ist S eine Teilmenge von E, also gilt die Behauptung.
Sei nun s > 0. Sei v einer der Vektoren, der zu S, aber nicht zu E
gehört. Bilde S' = S-{v} - dies ist eine
linear unabhängige Teilmenge von V, nach dem Ergänzungssatz gibt es
also eine Teilmenge E' von E, sodass die Vereinigungsmenge
S'∪E' eine Basis ist (dabei kann man voraussetzen, dass dies
eine disjunkte Vereinigung ist).
Da S' kein Erzeugendensystem ist (denn v liegt nicht in < S' >),
kann E' nicht leer sein.
Also gilt: |S| ≤ |S'∪E'|.
Andererseits ist die Anzahl der Elemente von S'∪E', die
nicht zu E gehören gleich s-1. Nach Induktion gilt demnach
|S'∪E'| ≤ |E|.
Insgesamt haben wir gezeigt:
|S| ≤ |S'∪E'| ≤ |E|.
Beweis des Nachsatzes: Sind B und B zwei endliche Basen,
so gilt |B| ≤ |B'|, da B eine linear
unabhängige Teilmenge und B' ein Erzeugendensystem ist.
Entsprechend gilt aber auch |B'| ≤ |B|.
Es bleibt zu zeigen, dass es in V keine unendliche Basis geben kann.
Wir wissen, dass V eine endliche Basis B besitzt. Sei n = |B|.
Gäbe es eine unendliche Basis B', so betrachte eine Teilmenge S
von B' der Kardinalität n+1. Es ist S eine linear
unabhängige Teilmenge von V, also ist
|S| ≤ n, Widerspruch.
Ist V ein endlich-erzeugter Vektorraum, so nennt man die
Kardinalität n einer (und daher jeder) Basis die Dimension von V und
man schreibt dim V = n und nennt V einen n-dimensionalen Vektorraum. Ist V nicht
endlich-erzeugt, so nennt man V auch "unendlich-dimensional" und schreibt
dim V = ∞.
Die oben notierte "wichtige Folgerung" lässt sich folgendermaßen
formulieren:
| In einem n-dimensionalen Vektorraum sind je
n+1 Vektoren linear abhängig.
|
Folgerung.
Sei V ein Vektorraum der Dimension n. Sei M eine Teilmenge von V der
Kardinalität n. Dann sind die folgenden Aussagen äquivalent:
- M ist eine Basis.
- M ist ein Erzeugendensystem.
- M ist linear unabhängig.
|
Beweis: Ist M ein Erzeugendensystem, so gibt es eine Teilmenge M'
von M, die eine Basis ist. Aber alle Basen haben die Kardinalität n.
Also M' = M und demnach ist M eine Basis.
Ist M linear unabhängig, so gibt es eine Obermenge M"
von M, die eine Basis ist. Aber alle Basen haben die Kardinalität n.
Also M" = M und demnach ist M eine Basis.
In vielen Büchern wird als erstes ein sogenannter Steinitz'scher
Austausch-Satz (oder Austausch-Lemma)
bewiesen - man stellt aber fest, dass es zwei ganz verschiedene
Aussagen sind, die unter diesem Namen formuliert werden.
(Fischer bringt die Aussage (1), Jänich die Aussage (2).)
Hier sollen beide
Aussagen als Folgerungen der oben bewiesenen Ergebnisse notiert werden.
Folgerung: Steinitz'scher Austauschsatz.
Sei V ein Vektorraum. Sei B ={b1,...,bn} eine
Basis von V
- Ist w ≠ 0 ein Element von V, so gibt es einen Index s, sodass auch
{b1,...,bs-1,bs+1,...,bn,w}
eine Basis ist.
(Hier wird also ein geeignetes
Basiselement bs gegen ein
vorgegebenes Element w ausgetauscht.)
Genau gilt: Schreibt man w = Σ λivi,
und ist λs ≠ 0, so kann man bs durch w ersetzen.
- Ist E ein Erzeugendensystem von V, und 0 ≤ s ≤ n, so gibt
es ein w in E, sodass
{b1,...,bs-1,bs+1,...,bn,w}
eine Basis ist.
(Hier wird also ein vorgegebenes
Basiselement bs gegen ein
geeignetes Elemente w ausgetauscht.)
|
Beweis:
Beide Aussagen folgen aus dem Ergänzungssatz und der Tatsache, dass alle
Basen die gleiche Kardinalität haben:
Beweis von (1): Es ist {w} eine linear unabhängige Menge. Ergänze
{w} durch eine Teilmenge E' von E zu einer Basis.
Die Menge E' muss die Kardinalität n-1 haben.
Beweis von (2): Hier betrachtet man die linear unabhängige Menge
{b1,...,bs-1,bs+1,...,bn}
und ergäzt sie durch eine Teilmenge E' von E zu einer
Basis. Da die neue Basis wieder die Kardinalität n haben muss, ist
E' einelementig.
Zur verschärften Fassung von (1): Ist w = Σ λivi
und λs ≠ 0, so ist w nicht in
< b1,...,bs-1,bs+1,...,bn >,
also ist die Menge
{b1,...,bs-1,bs+1,...,bn,w} eine
linear unhängige Teilmenge der Kardinalität n, und demnach eine
Basis.
Basiswechsel
Seien V = {v1,...,vn} und
W = {w1,...,wn} Basen des Vektorraums V.
Schreibe vj als Linearkombination der wi, etwa
vj = Σi aijwi
und bilde die Matrix mit den Koeffizienten aij:
|
TWV = (aij)ij
mit
vj = Σi aijwi
|
Man nennt TWV die
Transformationsmatrix des Basiswechsels.
Hat v in V die Koordinaten
v = Σj λjvj =
Σi μiwi
so ist
TWV λ = μ
|
(hier ist λ der Spaltenvektor mit Koeffizienten λj, entsprechend ist
μ der Spaltenvektor mit Koeffizienten μi
Die Transformationsmatrix beschreibt also gerade die
Koordinatentransformation beim Übergang von der Basis
V zur Basis W.
Dies ist eine ganz einfache Rechnung:
Σi μiwi =
Σj λjvj =
Σij λj
aijwi
= Σij
aijλj wi
Der Koeffizient von wi ist
- links: μi,
- rechts: Σj
aijλj.
Also ist Σj
aijλj = μi,
und dies ist gerade
die i-te Zeile von
TWV λ = μ.
Rechenregeln
- Sind V, W Basen von V, so ist
TVW =
(TWV)-1
- Seien U, V, W Basen von V. Dann ist
TWU
= TWV
TVU
- Sei V = {v1,...,vn}
eine Basis von Kn, und
E die Standard-Basis von Kn, so ist
TEV die (n×n)-Matrix,
deren Spalten gerade die Vektoren vi sind.
Insgesamt gilt also: Sind V = {v1,...,vn}
und W = {w1,...,wn} Basen von Kn,
so ist
TWV =
(TEW)-1
TEV,
und die
Matrix TEV hat die Vektoren vi
als Spalten,
die
Matrix TEW hat die Vektoren wi
als Spalten.
|
Beispiel.
Betrachte im R2 die beiden Basen
- V = {[3,-1],[1,2]}
- W = {[5,1],[4,1]}
Die Basiswechselmatrix lautet
|
TWV =
| 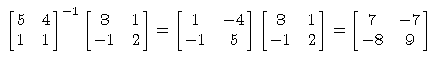
|
Der Vektor [4,1] hat im Koordinatensystem
V die Koordinaten [1,1], im Koordinatensystem W dagegen
die Koordinaten [0,1], und es ist wirklich
TWV([1,1]) = [0,1].
Und:
Der Vektor [5,3] hat im Koordinatensystem
V die Koordinaten [1,2], im Koordinatensystem W dagegen
die Koordinaten [-7,10], und es ist wirklich
TWV([1,2]) = [-7,10].
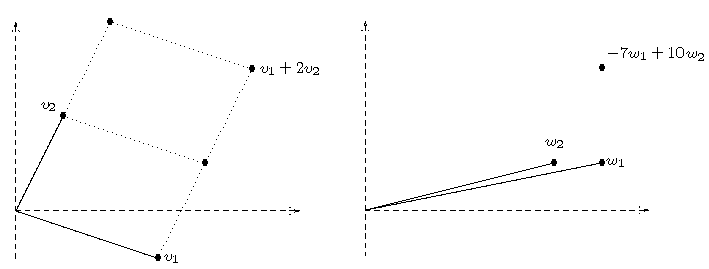
Beliebige Vektorräume
Ganz allgemein gilt (nicht nur für endlich erzeugte Vektorräume):
Satz: Jeder Vektorraum besitzt eine
Basis und je zwei Basen haben die gleiche Kardinalität.
Also gilt:
- Jeder Vektorraum lässt sich koordinatisieren.
- Jeder Vektorraum ist zu einem Standard-Vektorraum
isomorph.
Um diesen Satz zu beweisen, muss man das "Auswahlaxiom" verwenden.
Einen Beweis findet man zum Beispiel im Buch von Kowalsky.
|
Fakultät für Mathematik, Universität Bielefeld
Verantwortlich: C.M.Ringel
E-Mail:
ringel@mathematik.uni-bielefeld.de