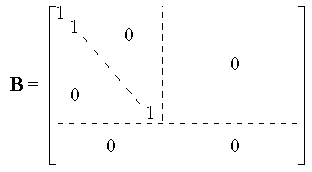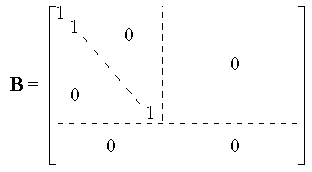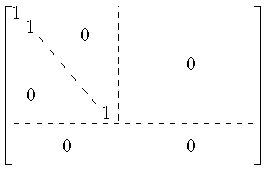Lineare Abbildungen

(Dies ist sicher der wichtigste Begriff der linearen Algebra!)

Definitionen

Sei K ein Körper, seien V, W K-Vektorräume.

Eine Abbildung f : V → W heißt linear falls gilt:

f(v+v') = f(v)+f(v') für alle v,v' in V.
f(λv) = λf(v) für alle v in V und alle λ in K.

Ist f : V → W linear, so gilt:

f(0) = 0,
f(-v) = - f(v) für alle v in V.
Ist U Unterraum von V, so ist f(U) Unterraum von W.
Ist U' Unterraum von W, so ist f^-1(U') Unterraum von V.

(Statt von einer "linearen Abbildung" spricht man oft auch von einer linearen Transformation oder einem Homomorphismus von Vektorräumen).

Kern und Bild

Sei f : V → W linear.

Definition: Kern(f) = { v in V | f(v) = 0 } (= f^-1(0)).
Definition: Bild(f) = { f(v) | v in V} (= f(V)).

(Statt Ker(f) schreiben viele Ker(f) oder ker(f), statt Bild(f) wird of Im(f) (dabei steht "ker" für "kernel", "im" für "image".)

Kern(f) ist ein Untervektorraum von V,
Bild(f) ist ein Untervektorraum von W.

Trivial ist: Genau dann ist f surjektiv, wenn Bild(f) = W gilt.
Nicht ganz trivial dagegen ist: Genau dann ist f injektiv, wenn Kern(f) = 0 gilt.

Ist f injektiv, so ist trivialerweise Kern(f) = 0.
Ist Kern(f) = 0, und ist f(v) = f(v'), so ist f(v-v') = 0, also v-v' in Kern(f) = 0, also v = v'.

Wichtig: Sei f : V → W linear. #
Unter f wird die Linearkombination Σ_i λ_iv_i auf die Linearkombination Σ_i λ_if(v_i) abgebildet:

f(Σ_i λ_iv_i) = Σ_i λ_if(v_i)
(alle v_i in V, alle λ_i in K, nur endlich viele λ_i von Null verschieden)

Es folgt:

Ist v_i (i in I) ein Erzeugendensystem von V, so ist f(v_i) (i in I) ein Erzeugendensystem von Bild(f).
Ist die Famile v_i (i in I) in V linear abhängig, so ist die Familie f(v_i) (i in I) in V linear abhängig,

Beispiele

Die identische Abbildung 1_V : V → V ist linear (es ist 1_V durch 1_V(v) = v für alle v in V definiert).
Das Differenzieren
- Sei F der R-Vektorraum aller Funktionen I → R,
  Sei D der R-Vektorraum aller differenzierbaren Funktionen I → R,
  Die Abbildung D → F, die der Funktion f ihre Ableitung f' zuordnet, ist R-linear.
Das Integrieren mit festem Basispunkt.

Der Dimensionssatz für lineare Abbildungen

Satz (Dimensionssatz für lineare Abbildungen).
Seien V, W Vektorräume, sei f : V → W eine lineare Abbildung.
Ist V endlich erzeugt, so sind auch Kern(f) und Bild(f) endlich erzeugt und es gilt

dim Kern(f) + dim Bild(f) = dim V.

Man nennt dim Bild(f) den Rang von f. Also kann man auch schreiben:

dim Kern(f) + Rang(f) = dim V.

Folgerung: Seien V, W Vektorräume der Dimension n. Sei f : V → W eine lineare Abbildung. Dann sind die folgenden Aussagen äquivalent:

f ist injektiv,
f ist surjektiv,

Wir werden weiter unten zeigen, dass derartige lineare Abbildung "Isomorphismen" sind.

Und auch umgekehrt: Ist f surjektiv, so ist dim Bild(f) = dim W = dim V, also ist dim Kern(f) = 0, und demnach f injektiv.

"Freiheit"

Sei V ein Vektorraum mit Basis B. Ist eine lineare Abbildung f : V → W gegeben, so ist f eindeutig durch die Werte f(b) bestimmt, andererseits kann man derartige Werte beliebig vorschreiben! Dies gerade besagt der folgende Satz:

"Freiheit" Sind V, W K-Vektorräume und ist B = {b_i | i in I} eine Basis von V mit Indexmenge I, so entsprechen die linearen Abbildungen f : V → W bijektiv den mengentheoretischen Abbildung I → W, auf folgende Weise: der linearen Abbildung f : V → W entspricht die Zuordnung, die jedem i in I den Vektor f(b_i) zuordnet.
Betrachtet wird hier also

Hom(V,W) für die Menge der linearen Abbildungen V → W,
Abb(I,W) für alle Abbildungen von I in W (aufgefasst einfach als Menge))
und

die Bijektion

Hom(V,W) → Abb(I,W)
bei der f in Hom(V,W) die Einschränkung f|B zugeordnet wird, dies ist eine mengentheoretische Abbildung B → W (oder eben I → W).

Die Injektivität der Zuordnung besagt:
Eine lineare Abbildung f ist eindeutig durch die Werte f(b_i) bestimmt.
Die Surjektivität der Zuordnung besagt:
Man kann diese Werte beliebig vorschreiben.
Oder auch, anders formuliert:
Ist jedem i in I der Vektor v_i zugeordnet, so wird durch f(Σ λb_i) = Σ λv_i eine lineare Abbildung f : V → W definiert (und man erhält auf diese Weise alle linearen Abbildungen).

Die Wortwahl "Freiheit" erklärt sich so:
Die Surjektivität der Zuordnung besagt:
Man kann Werte beliebig vorschreiben.
Es ist diese "Wahlfreiheit" der Grund, worum man eine Basis auch ein freies Erzeugendensystem nennt, daher der Name "Freiheit".

Surjektivität: Ist zu jedem i in I ein w_i in W gewählt, so definieren wir f : V → W durch f(Σ λb_i) = Σ λv_i.

Da jedes v in V sich als Linearkombination der b_i schreiben lässt, ist f auf ganz V definiert - und f ist "wohldefiniert", da sich jedes v in V nur auf eine Weise in der Form Σ λb_i schreiben lässt!.
Es bleibt zu zeigen, dass das so definierte f linear ist ...

Komposition von linearen Abbildungen

Sind die Abbildungen f : V' → V, g : V → V" linear, so ist auch die Komposition gf linear.

Rang-Abschätzung für Komposition von linearen Abbildungen. Sind lineare Abbildungen f : V' → V, g : V → V" gegeben, und ist dim V = n, so gilt:
Rang(f)+Rang(g)-n ≤ Rang(gf) ≤ min(Rang(f),Rang(g))

Wegen des Dimensionssatzes für lineare Allbildungen, angewandt auf h, gilt:

dim Bild(gf) = Bild(h) = Bild(f) - dim Kern(h).

dim Bild(gf) ≤ Bild(f).

dim Bild(gf) ≤ Bild(g).

Andererseits sehen wir:

dim Bild(gf) = dim Bild(h) = dim Bild(f) - dim Kern(h) ≥ dim Bild(f) - Kern(g) = Bild(f) + Bild(g) - n,

Isomorphismen

Kriterium 1. Seien V, W Vektorräume, sei f : V → W linear.
Dann sind die folgenden Aussagen äquivalent:

Bild(f) = W und Kern(f) = 0.
f ist bijektiv.
Es gibt eine lineare Abbildung g : W → V mit gf = 1_V und fg = 1_W.

Wenn diese Bedingungen erfüllt sind, so nennt man f einen Isomorphismus.

Zusatz. Die in (3) gesuchte Abbildung g ist durch f eindeutig bestimmt und ist gerade die mengentheoretische Umkehrabbildung.

Sei also f bijektiv. Dann ist die mengentheoretische Umkehrabbildung f^-1 definiert. Zu zeigen ist, dass f^-1 linear ist, dass also gilt

f^-1(w+w') = f^-1(w) + f^-1(w'),
f^-1(λw) = λf^-1(w)

^-1

Entsprechend wenden wir f auf λf^-1(w) an:
f( λf^-1(w)) = λff^-1(w) = λw = ff^-1(λw). Auch hier verwenden wir die Injektivität von f, und erhalten (b).

Es gilt natürlich f^-1f = 1_V und ff^-1 = 1_W. Demnach gilt also (3) mit g = f^-1.

Dass g durch die Gleichungen gf = 1_V und fg = 1_W eindeutig bestimmt ist, sieht man wie üblich: Ist auch g'f = 1_V, so ist g' = g' 1_W = g'fg = 1_Vg = g.

Es bleibt zu zeigen: (3) impliziert (2). Aber dies ist eine rein mengentheoretische Implikation und sollte bekannt sein!

Gibt es einen Isomorphismus f : V → W, so nennt man die Vektorräume V und W isomorph.

Kriterium 2. Seien V, W Vektorräume, sei f : V → W linear. Sei v_i mit i in I eine Basis von V.
Dann sind die folgenden Aussagen äquivalent:

f ist ein Isomorphismus.
Die Familie f(v_i) mit i in I ist eine Basis von W.

Ist v_i mit i in I linear unabhängig in V, und ist eine Linearkombination Σ_i λ_if(v_i) = 0, so wende die Umkehrabbildung f^-1 an: Wir erhalten Σ_i λ_iv_i = 0, also sind alle λ_i = 0.

(2) impliziert (1): Offensichtlich ist f surjektiv, denn jedes Element in W ist Linearkombination der Vektoren f(v_i), also Bild unter f einer Linearkombination der Vektoren v_i.

Ist v in Kern(f), so schreibe v als Linearkombination der v_i. Wende f an: wir erhalten eine Linearkombination der f(v_i), die Null ist. Da die f(v_i) linear unabhängig sind, sind alle Koeffizienten 0.

Folgerung aus Kriterium 2. Seien V, W isomorphe Vektorräume. Ist V endlich-erzeugt, so ist auch W endlich erzeugt und dim V = dim W.

Beweis: Sei f : V → W ein Isomorphismus. Eine Basis von V wird auf eine Basis von W abgebildet, also haben V und W Basen mit gleicher Kardinalität.

Erste Folgerung aus der "Freiheit":

Folgerung 1 aus der "Freiheit": die Koordinatisierungsabbildung Φ_B.

Ist B = { b₁, ..., b_n} eine Basis von V, so erhalten wir eine (und nur eine) lineare Abbildung

Φ_B : Kⁿ → V mit Φ_B(e_i) = b₁,

und dies ist ein Isomorphismus.

ⁿ

Folgerung 1'. Jeder Vektorraum der Dimension n ist isomorph zu Kⁿ.

Folgerung 1". Alle Vektorräume der Dimension n sind zueinander isomorph.

ⁿ

^-1

Basiswechsel

Man erhält die Basiswechsel-Matrix T^V_W als Matrix zur Hintereinanderschaltung der folgenden linearen Abbildungen

T^V_W = Φ_W^-1Φ_V

Lineare Abbildungen und Matrizen

Beschränkt man sich auf endlich-erzeugte Vektorräume, so gibt es eine klare Entsprechung zwischen linearen Abbildungen und Matrizen - dies wird in den hellblau-unterlegten Feldern thematisiert:
Es gibt eine Art Wörterbuch, wie Begriffe der abstrakten linearen Algebra den Begriffen der Matrizentheorie entsprechen. Die hellblau-unterlegten Felder zeigen dies.

Jede (m×n)-Matrix A mit Koeffizienten in K liefert eine lineare Abbildung f_A : Kⁿ → K^m, die durch

f_A(v) = Av
(Matrizen-Multiplikation; wir fassen v als Spaltenvektor auf).
definiert ist.
Sind A, B (m×n)-Matrizen mit Koeffizienten in K, und ist f_A = f_B, so ist A = B.

Folgerung 2 aus der "Freiheit": Es gilt auch die Umkehrung!
Zu jeder linearen Abbildung f : Kⁿ → K^m gibt es eine (m×n)-Matrix A = M(f) mit Koeffizienten in K, sodass gilt f = f_A.

Umformulierung:
Die Zuordnung, die einer Matrix A in M(m×n,K) die Abbildung f_A zuordnet ist eine Bijektion zwischen

M(m×n,K)
und
der Menge der linearen Abbildungen f : Kⁿ → K^m

Merkregel für die Bestimmung der Matrix A = M(f).
Der linearen Abbildungen f : Kⁿ → K^m wird die (m×n)-Matrix A = M(f) zugeordnet, mit

die j-te Spalte von A ist f(e_j).

ⁿ

Komposition. f_AB = f_Af_B Also: Die Matrizen-Multiplikation (links) entspricht der Hintereinanderschaltung von Abbildungen (rechts).
Invertierbarkeit von Matrizen.
Ist A in M(m�n,K), B in M(n�m,K) mit AB = I_m und BA = I_n, so ist m = n.

ⁿ

Kern, Bild, Rang

Kern(f_A) = Loes(A,0),
Bild(f_A) = C(A) (der von den Spalten erzeugte Unterraum)
Rang(f_A) = Rang(A)

Genau dann ist f_A injektiv, wenn die Spalten von A linear unabhängig sind.
Genau dann ist f_A surjektiv, wenn die Spalten von A den Raum K^m erzeugen.
Genau dann ist f_A bijektiv (also ein Isomorphismus, wenn die Spalten von A eine Basis bilden, also genau dann, wenn die Matrix A invertierbar ist.

Das Zusammenspiel der Folgerungen 1 und 2:

Seien V, W Vektorräume, sei dim V = n, dim W = m. Sei V eine Basis von V, W eine Basis von V. Dann erhalten wir eine Bijektion zwischen den linearen Abbildungen f : V → W und den (n×m)-Matrizen mit Koeffizienten in K durch

A wird zugordnet Φ_W f_AΦ_V^-1
f wird zugeordnet die Matrizendarstellung von Φ_W^-1f Φ_V.

f_A
Kⁿ → K^m
↓Φ_V ↓Φ_W
V → W
f

Ist f_A = Φ_W^-1 f Φ_V, so schreiben wir A = M^V_W(f) und sagen, dass A die darstellende Matrix von f bezüglich der Basen V und W ist.
Ist f : Kⁿ → K^m linear und bezeichnen wir mit E jeweils die Standard-Basis von Kⁿ wie auch von K^m, so ist M^E_E(f) = M(f).

Ist V = {v₁,...,v_n} eine Basis von Kⁿ (aufgefasst als Raum von Spaltenvektoren), so sei M(V) die Matrix, deren j-te Spalte gerade v_j ist.
Dann gilt:

M(V) = M(Φ_V)

dies ist die darstellende Matrix von Φ_V.

Nun sei A eine (m×n)-Matrix mit Koeffizienten in K. Betrachte die Abbildung f_A. Basiswechsel in Kⁿ und K^m liefert:

	f_B
Kⁿ	→	K^m
↓Φ_V		↓Φ_W
Kⁿ	→	K^m
	f_A

Also die Matrizengleichung:

B = M(W)^-1A M(V).

Auswertung des Beweises der Dimensionsformel:

Satz. Seien V, W endlich-erzeugte Vektorräume, sei f : V → W lineare Abbildung. Dann gibt es Basen V von V und W von W mit M^V_W(f) = B mit

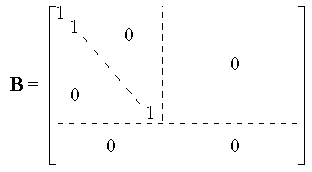
Wenden wir diesen Satz auf eine Abbildung der Form f_A an, wobei A eine (m×n)-Matrix mit Koeffizienten in K ist, so erhalten wir einen neuen Beweis von Satz 1"".

Man vergleiche die beiden Beweise: Unser erster Beweis von Satz 1"" verwendete elementare Zeilen- und Spalten-Operationen und ist konstruktiv (ist die Matrix A gegeben, so weiss man ganz genau, wie man tun muss, um A in die angegebene Form zu bringen). Der neue Beweis dagegen ist elegant, aber nicht direkt konstuktiv: er basiert auf Begriffen wie Unterraum und Basis, und auf vor allem dem Ergänzungssatz.

Sei b₁,...,b_s eine Basis von Kern(f),
Setze dies fort durch a₁,...,a_r zu einer Basis von V.
Dann ist f(a₁),...,f(a_r) eine Basis von Bild(f)
(Dies besagt gerade der Beweis der Dimensionsformel für lineare Abbildungen; insbesondere ist r = Rang(f).)
Setze f(a₁),...,f(a_r) durch c₁,...,c_t fort zu einer Basis von W.

₁

Sei K ein Körper. Seien A, B (m×n)-Matrizen mit Koeffizienten in K. Dann sind die folgenden Aussagen äquivalent:

Es gibt Vektorräume V, W und eine lineare Abbildung f : V → W, so dass A und B darstellende Matrizen von f (bezüglich irgend welcher Basen) sind.
f_B ist darstellende Matrix von f_A (bezüglich einer Basis V von Kⁿ und einer Basis W von K^m.
Es gibt invertierbare Matrizen P, Q mit PAQ = B.
A, B haben den gleichen Rang.

Man nennt in diesem Fall die Matrizen A und B äquivalent.. (Meist nimmt man die Aussage (3) als Definition der Äquivalenz von Matrizen.)

Die Äquivalenz zwischen diesen Aussagen und der Aussage (4) ist tiefliegender: Gilt (1), so haben A und B den gleichen Rang, denn Rang(A) = Rang(f) und Rang(B) = Rang(f), also gilt (4).
Gilt umgekehrt (4), so haben wir gerade gesehen, dass sowohl f_A als auch f_B die gleiche darstellende Matrix besitzen:

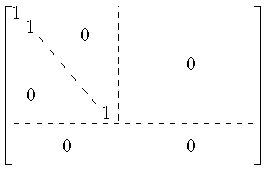
Fakultät für Mathematik, Universität Bielefeld
Verantwortlich: C.M.Ringel
E-Mail: ringel@mathematik.uni-bielefeld.de