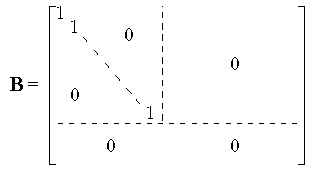
Wenden wir dies auf eine Abbilung der Form fA an, wobei A eine (m×n)-Matrix mit Koeffizienten in K ist, so erhalten wir Satz 1"".
Nun sei A eine (m×n)-Matrix mit Koeffizienten in K. Betrachte die Abbildung fA. Basiswechsel in Kn und Km liefert:
| fB | ||||
| Kn | → | Km | ||
| ↓ΦV | ↓ΦW | |||
| Kn | → | Km | ||
| fA |
| B = M(W)-1A M(V). |
Auswertung des Beweises der Dimensionsformel:
Satz. Seien V, W endlich-erzeugte
Vektorräume, sei f : V → W lineare Abbildung. Dann
gibt es Basen V von V und W von W
mit MVW(f) = B mit
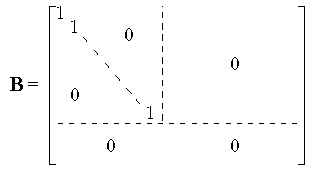
Wenden wir dies auf eine Abbilung der Form fA an, wobei A eine (m×n)-Matrix mit Koeffizienten in K ist, so erhalten wir Satz 1"". |
Sei K ein Körper. Seien A, B (m×n)-Matrizen mit Koeffizienten in K.
Dann sind die folgenden Aussagen äquivalent:
|
Die Äquivalenz zwischen diesen Aussagen und der Aussage (4) ist tiefliegender:
Gilt (1), so haben A und B den gleichen Rang, denn Rang(A) = Rang(f) und
Rang(B) = Rang(f), also gilt (4).
Gilt umgekehrt (4), so haben wir gerade gesehen, dass sowohl fA
als auch fB die gleiche darstellende Matrix besitzen:
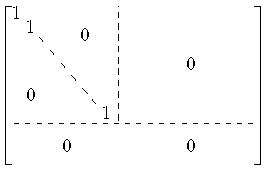
| TVW = ΦW-1ΦV |