Definitionen

• ~ heißt reflexiv, falls h ~ h für alle h in H gilt.
• ~ heißt symmetrisch, falls gilt: sind h,h' Elemente aus H mit h ~ h', so ist h' ~ h.
• ~ heißt antisymmetrisch falls gilt: sind h,h' Elemente aus H mit h ~ h' und h' ~ h, so ist h = h'.
• ~ heißt transitiv, falls gilt: sind h,h',h" Elemente aus H mit h ~ h' und h' ~ h", so ist h ~ h".

Eine Halbordnung (H,≤) ist eine Menge H zusammen mit einer Relation ≤, die reflexiv, transitiv und antisymmetrisch ist. Sei nun (H,≤) eine Halbordnung. Ist h≤h' und h≠h', so schreibt man h < h'.

• Man schreibt h" = h∨h', falls gilt:
  • Es ist h ≤ h", h' ≤ h".
  • Ist g in H mit h ≤ g und h' ≤ g, so ist h" ≤ g.
• und man schreibt h" = h∧h', falls gilt:
  • Es ist h" ≤ h, h" ≤ h'.
  • Ist g in H mit g ≤ h' und g ≤ h', so ist g ≤ h".

Eine endliche Halbordnung (H,≤) veranschaulicht man sich oft, indem man das zugehörige Hasse-Diagramm zeichnet: Man zeichnet Knoten (= Punkte, meist fett gezeichnet) und Kanten (also Verbindungstrecken zwischen zwei solchen Knoten), dabei verlaufen die Kanten nie horizontal:
• Für jedes h in H zeichnet man einen Knoten; gilt h < h' so verlangt man, dass h unterhalb von h' liegt.
• Sind h ≠ h' in H, so verbindet man h, h' durch eine Kante, falls gilt: Einerseits ist h≤h', andererseits folgt aus h≤g und g≤h' dass h=g oder h'=g gilt
  (man nennt dann h, h' Nachbarn in H).

Hier als Beispiel die Halbordnung (H,≤) mit H = {a,b,c,d,e,f,g}, wobei a,b,c,d,e,f,g paarweise verschieden sind, und ≤ sei die Teilmenge {(a,b), (a,c), (b,c), (d,f), (e,f), (e,g)} ⊆ H×H. (Es ist hier d∨e = f und f∧g = e. Dagegen sind zum Beispiel a∧d und a∨d nicht definiert.)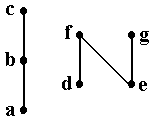

Weiterführende Bemerkung. Ist (H,≤) ein Verband, so gelten die folgenden Eigenschaften für alle a,b,c in H: a∧a = a,   a∨a = a   (Idempotenz) a∧b = b∧a,   a∨b = b∨a  (Kommutativität) (a∧b)∧c = a∧(b∧c) ,   (a∨b)∨c = a∨(b∨c)   (Assoziativität) a∧(a∨b) = a,   a∨(a∧b) = a   (Absorptionsgesetz) Man kann diese Eigenschaften auch nehmen, um Verbände axiomatisch in der Form (H,∨,∧) zu definieren: Man sagt dann also: ein Verband (H,∨,∧) ist eine Menge H mit zwei Verknüpfungen ∨ und ∧ auf H, so dass folgende Axiome gelten: Für alle a,b,c in H ist a∧a = a,   a∨a = a   (Idempotenz) a∧b = b∧a,   a∨b = b∨a  (Kommutativität) (a∧b)∧c = a∧(b∧c) ,   (a∨b)∨c = a∨(b∨c)   (Assoziativität) a∧(a∨b) = a,   a∨(a∧b) = a   (Absorptionsgesetz) Und man definiert dann ≤ durch: h ≤ h' falls gilt: h ∨ h' = h' (und aus den Axiomen folgt: genau dann ist h∨h' = h', wenn h∧h' = h).

Sei K ein Körper und V ein K-Vektorraum. Die Menge der Unterräume von V bildet (bezüglich der Inklusion) einen modularen Verband.

Beweis.