Unterräume
Vorausgesetzt wird der Dimensionsbegriff
(und die Definition von Durchschnitt und Summe zweier Unterräume).
Dimension von Unterräumen
Sei V ein endlich erzeugter Vektorraum, sei
U ein Unterraum von V.
- Auch U ist endlich erzeugt.
- dim U ≤ dim V
- Ist dim U = dim V, so ist U = V.
|
Jede linear unabhängige Teilmenge in V hat Kardinalität höchstens n,
insbesondere gilt dies für die linear unabhängigen Teilmenge in U,
also gibt es linear unabhängige Teilmengen in U mit maximaler
Kardinalität m. Sei S eine derartige Teilmenge. Es ist < S >
ein Unterraum von U. Wäre dies ein echter Unterraum, so wähle ein u in
U, das nicht zu < S > gehört: Dann ist S∪{u} eine
linear unabhängige Teilmenge von U der Kardinalität m+1.
Dies geht nicht. Also ist < S > = U. Insbesondere
ist U endlich erzeugt und dim U = m ≤ n.
Ist m = n, so ist S eine linear unabhängige Teilmenge von V der
Kardinalität n, also eine Basis von V. Also ist U = V.
Die Dimensionsformel für Paare von Unterräumen.
Satz. Seien U, U' endlich-erzeugte Unterräume eines Vektorraums.
Dann sind auch die Unterräume U+U' und U∩U' endlich erzeugt und es
gilt
| dim U + dim U' = dim U∩U' + dim U+U'.
|
|
Beweisidee: Dass die Unterräume
U+U' und U∩U' ebenfalls endlich erzeugt sind, ist offensichtlich:
U∩U' ist ein Unterraum des endlich erzeugten Unterraums U, also endlich
erzeugt; ist S ein Erzeugendensystem von U und S'
ein Erzeugendensystem von U', so ist die Vereinigung von
S und S' ein Erzeugendensystem von U+U'.
Um die Dimensionsformel zu beweisen,
wähle eine Basis von U∩U', setze sie fort:
einerseits zu einer Basis von U, andererseits zu einer Basis von U'.
Behauptung: Die Vereinigungsmenge dieser beiden Basen ist eine Basis von U+U'.
Natürlich ist dies ein Erzeugendensystem von U+U'; es ist also nur die
lineare Unabhängigkeit nachzuweisen...
Tripel von Unterräumen
Seien U1, U2, U3 Unteräume des
Vektorraums V.
Es gilt:
- (U1+U2) ∩ U3 ⊇
(U1∩U3) + (U2∩U3)
- U1 + (U2∩U3) ⊆
(U1+U2) ∩ (U1+U2)
Das Beispiel V = K2,
- U1 = {(x,0) | x in K},
- U2 = {(x,x) | x in K},
- U3 = {(0,x) | x in K},
zeigt, dass üblicherweise keine Gleichheit gilt!
|
|
Satz (Modularität). Ist U1 in U3 enthalten,
so gilt
(Man kann demnach die Klammern weglassen!)
|
Beweis: Offensichtlich ist der Unterraum der rechten Seite in dem der
linken enthalten.
Um die umgekehrte Inklusion zu zeigen, muss man mit Elementen arbeiten:
Sei u1+u2 = u3 mit
ui in Ui für i=1,2,3.
Wegen u2 = u3-u1 gehört
u2 nicht nur zu U2, sondern auch zu U3
(wie die rechte Seite zeigt),
also zu U2∩U3. Demnach ist
u3 = u1+u2 in
U1+(U2∩U3).
|
Satz.
Sind drei Unterräume U1, U2, U3
eines Vektorraums V gegeben und ist U1 in U3 enthalten,
so ist die Menge
{ U1, U2, U3,
U1+U2,
U2+U3,
U1∩U2,
U2∩U3,
U1+U2∩U3 }
abgeschlossen unter Summenbildung und unter Durchschnittsbildung.
|
Unter der Voraussetzung U1 ⊆ U3 kann man also aus den
Unterräumen
U1, U2, U3 mit Hilfe der
Operationen + und ∩ nur 5 weitere Unterräume konstruieren!
Man erhält folgendes Bild, in dem diese 8 Unterräume (und 0 und V)
zusammen mit den immer gültigen Inklusionen eingetragen sind:
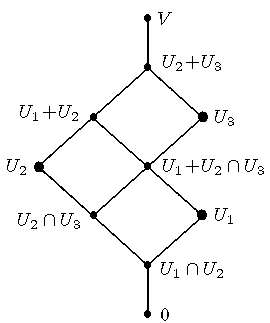
Hier haben wir einen
"Unterraum-Verband" gezeichnet:
- die Knoten
symbolisieren Unterräume von V;
- sind zwei Knoten durch eine Kante verbunden, so ist der untenstehende
Raum im darüberstehenden Raum enthalten.
- Mit je zwei Unteräumen V' und V" ist V'+V" eingezeichnet, und zwar
mit aufwärtsgerichteten Kantenzügen von V' nach V'+V" und
von V" nach V'+V".
- Mit je zwei Unteräumen V' und V" ist V'∩V" eingezeichnet, und zwar
mit aufwärtsgerichteten Kantenzügen von V'∩V" nach V' und
von V'∩V" nach V".
Zum Beweis zeigt man:
- Erstens: für jede gezeichnete Kante gilt die
entsprechende Inklusion. (Dies ist ganz einfach!)
- Zweitens ist zu zeigen, dass für je zwei
Knoten V', V", sowohl V'+V" als auch V'∩V" mit den entsprechenden
Kantenzügen eingetragen ist.
(Man erschrickt zuerst, denn es gibt ja
10 Knoten, also 100 Knotenpaare (V',V") - aber man braucht sich nur um
Knotenpaare (V',V") zu kümmern, die nicht durch einen nach oben gerichteten
Kantenzug verbunden sind. Denn ist V' ⊆ V", so ist V'+V" = V" und
V'∩V" = V'.
Es bleiben (bis auf Vertauschung) nur 5 Knotenpaare V', V" übrig, und zwar
- U1+U2, U3
- U2, U3
- U2, U1+U2∩U3
- U2, U1
- U2∩U3, U1
In allen fünf Fällen V',V" sieht man sehr einfach, dass V'+V"
und V'∩V" die gewünschte Eigenschaft haben.
Weiterführende Bemerkungen (ohne Beweis)
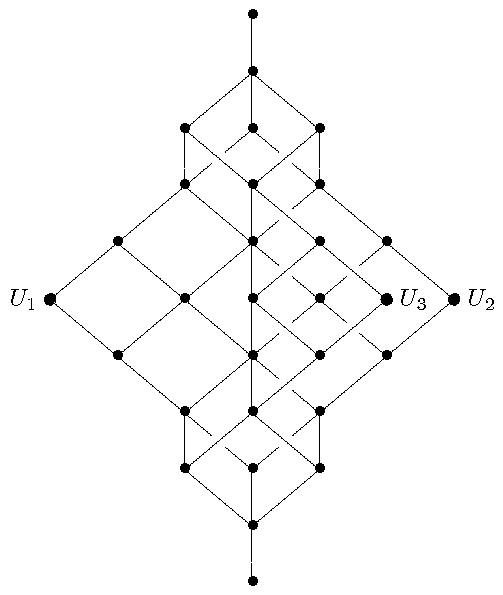
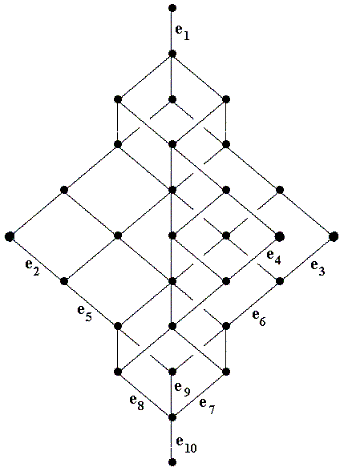
Hier der größt-mögliche Unterraum-Verband, der vom einem
Tripel von Unterräumen erzeugt werden kann:
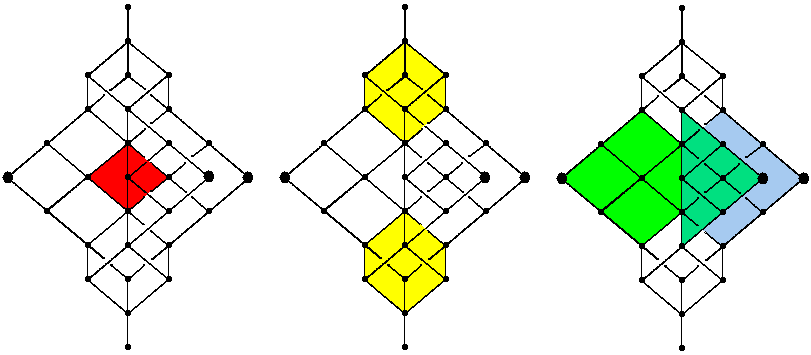
Zum besseren Einsicht sind in den folgenden drei Bildern einige
Unterverbände farbig markiert:
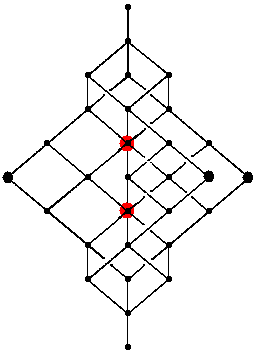
Von besonderem Interesse sind die folgenden beiden Knoten, da sie
neben den beiden untersten und den beiden obersten Knoten die einzigen
Knoten sind, die bei einer Vertauschung der Unterräume Ui
invariant bleiben. (Siehe Aufgabenzettel 11, Aufgabe 3):
Man kann diesen Verband auf folgende Weise realisieren: Sei K ein
Körper. Betrachte im K10 (mit Standard-Basis e1,...,
e10) die folgenden drei Unteräume:
- U1 = < e2, e5, e8,
e9, e10 >
- U2 = < e3, e6, e7,
e9, e10 >
- U3 = < e4, e5+e6,
e7,
e8, e10 >
Dann ist der von den Unterräumen U1, U2, U3
erzeugte Verband größt-möglich!
Im Bild rechts haben wir einigen Kanten Vektoren der
Standard-Basis zugeordnet: verbindet eine derartige Kante die Knoten V' ⊂ V",
so bedeutet die Angabe von ei dass gilt: V'+< ei > = V".
| 
|
|
Die Struktur dieses Verbandes
wurde im Jahr 1900 von Dedekind
publiziert (Über die von drei Moduln erzeugte Dualgruppe, Math. Ann.
53 (1900), 371-403.), es ist der "freie modulare Verband in drei
Erzeugenden".
Es ist unbekannt, wie das entsprechende Bild für vier
Unterräume U1, U2, U3, U4
aussehen könnte. Es ist leicht zu sehen, dass der "
"freie modulare Verband in vier Erzeugenden" unendlich viele Knoten hat,
man kennt einige Teilverbände, die ganz oben oder ganz unten sitzen
(die "cubicles" von Gelfand-Ponomarev), mehr aber nicht ...
The free modular lattice with three generators (which has twenty-eight
elements) is
a beautiful construct that is presently exiled from textbooks in
linear algebra.
Too bad, because the elements of this lattice explicitly
describe all projective invariants of three subspaces.
Gian-Carlo Rota (1997)
|
BIREP
Last modified: Sun Jan 9 10:03:47 CET 2005





