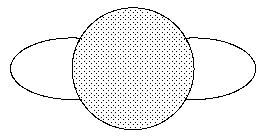
wie man den folgenden Skizzen entnimmt!
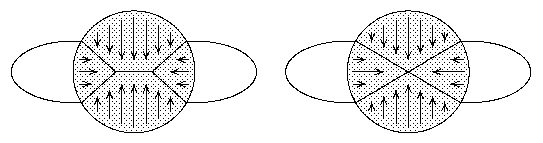
Für t=0 erhalten wir x, für t=1 erhalten wir r(x), und ist x in A, so ist r(x) = x, also auch tr(x)+(1-t)x = tx+(1-t)x = x.
Also setzen wir H(x,t) = tr(x)+(1-t)x.
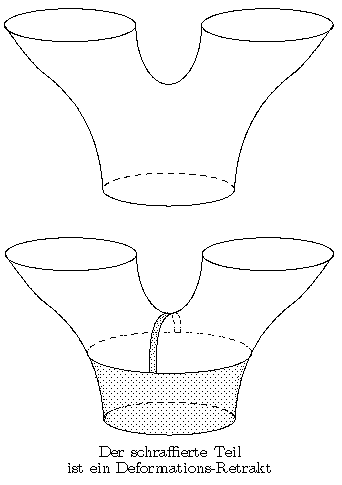
Auf diese Weise (und unter Verwendung von Beispiel 3) sieht man, dass der gegebene Raum homotopie-äquivalent zur punktierten Summe zweier Kreise ist!
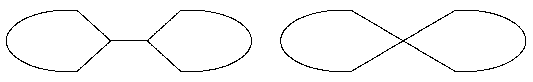
Beides sind Deformationsretrakte des gleichen Raums

wie man den folgenden Skizzen entnimmt!

Entsprechend zeigt man: Ist G ein endlicher Graph und sind x, y zwei verschiedene Ecken von G, die durch eine Kante K verbunden sind, so sind die Räume G und G/K homotopie-äquivalent.
Induktiv erhält man demnach: Ein endlicher zusammenhängender Graph ist zur punktierten Summe von endlich vielen Kreisen homotopie-äquivalent.