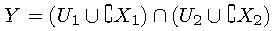- Beweis von b: Bezeichne den Durchschnitt von Y und Xi mit Ui, i=1,2. Zeige
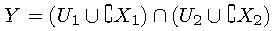
Da Xi abgeschlossen ist, ist das Komplement von Xi offen, also sind alle vier Mengen rechts offen, demnach ist auch Y offen.
Immer gilt (nach Definition): Ist U offen in X, so ist der Durchschnitt
von U mit Xi offen in Xi .
Wann gilt die Umkehrung?
Satz 1.
Seien X1 und X2 Unterräume von X, und X sei die
Vereinigung von X1 und X2.
Sei Y eine Teilmenge von X, und der
Durchschnitt von Y mit X1 und auch mit X2 sei jeweils
offen (in X1 bzw. in X2).
|