Numerische Spektralanalyse
unendlich-dimensionaler Transferoperatoren
07-014 Wolf-Jürgen Beyn, Sergey Piskarev.
Shadowing for discrete approximations of abstract parabolic equations
This paper is devoted to the numerical analysis of abstract semilinear
parabolic problems
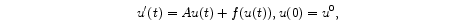
in some
general Banach space E. We prove a shadowing Theorem that compares
solutions of the continuous problem with those of a semidiscrete
apprximation (time stays continuous) in the neighborhood of a
hyperbolic equilibrium. We allow rather general discretization schemes
following the theory of discrete approximations developed by
F. Stummel, R.D. Grigorieff and G. Vainikko. We use a compactness
principle to show that the decomposition of the flow into growing and
decaying solutions persists for this general type of
approximation. The main assumptions of our results are naturally
satisfied for operators with compact resolvents and can be verified
for finite element as well as finite diference methods. In this way we
obtain a unified approach to shadowing results derived e.g. in the
finite element context ([19, 20, 21]).