Vorträge

Workshops

Seminare

  • Raphael Kruse (TU Berlin) : On randomized time-stepping methods for non-autonomous evolution equations with time-irregular coefficients
    18.02.2019, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk, we consider the numerical approximation of Carathéodory-type ODEs and of nonlinear and non-autonomous evolution equations whose coefficients may be irregular or discontinuous with respect to the time variable. In this non-smooth situation, it is difficult to construct numerical algorithms with a positive convergence rate. In fact, it can be shown that any deterministic algorithm depending only on point evaluations may fail to converge. Instead, we propose to apply randomized Runge-Kutta methods to such time-irregular evolution equations as, for instance, a randomized version of the backward Euler method. We obtain positive convergence rates with respect to the mean-square norm under considerably relaxed temporal regularity conditions. An important ingredient in the error analysis consists of a well-known variance reduction technique for Monte Carlo methods, the stratified sampling. We demonstrate the practicability of the new algorithm in the case of a fully discrete approximation of a parabolic PDE. This talk is based on joint work with Monika Eisenmann (TU Berlin), Mihály Kovács and Stig Larsson (both Chalmers University of Technology) as well as Yue Wu (U Edinburgh).

  • Christian Pötzsche (Alpen-Adria Universität Klagenfurt) : Numerical Dynamics of Integrodifference Equations
    17.07.2018, 16:15, U2-147, Oberseminar Numerik
    Abstract: Integrodifference equations (IDEs for short) are a popular tool in theoretical ecology to describe the spatial dispersal of populations with nonoverlapping generations. From a mathematical perspective, IDEs are recursions on ambient spaces of continuous or integrable functions and thus generate infinite-dimensional dynamical systems. Hence, for simulation purposes an appropriate numerical approximation yielding a finite-dimensional state space is due. Our goal is to study dynamical properties of IDEs (e.g. existence of reference solutions, attractors, invariant manifolds) which are preserved under corresponding numerical methods and to establish convergence for increasingly more accurate schemes.

  • Ingo Könemann : Stabilität nichtautonomer Differenzengleichungen
    06.07.2018, 14:15, V5-148, AG Dynamische Systeme
    Abstract:

  • Janosch Rieger (Monash University, Melbourne) : A Galerkin-type approach to shape optimisation in the space of convex sets
    25.06.2018, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk, I will discuss spaces of polytopes with fixed outer normals and their use in theoretical and practical shape optimization. These spaces possess a natural system of coordinates, and all admissible coordinates can be characterized by a linear inequality, which is handy both from an analytical as well as from a computational perspective.
    These polytope spaces approximate the space of all nonempty convex and compact subsets in Hausdorff distance uniformly on every bounded set, so they behave like classical Galerkin approximations to function spaces. I will show that for simple shape optimization problems, the set of global minimizers of auxiliary problems posed in the polytope spaces converges to the set of global minimizers of the original problem.

  • Evelyn Buckwar (JKU Linz) : A stability vs. Monte-Carlo integration problem for SDEs
    18.12.2017, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we investigate the interplay of almost sure and mean-square stability for linear SDEs and the Monte Carlo method for estimating the second moment of the solution process. In the situation where the zero solution of the SDE is asymptotically stable in the almost sure sense but asymptotically mean-square unstable, the latter property is determined by rarely occurring trajectories that are sufficiently far away from the origin. The standard Monte Carlo approach for estimating higher moments essentially computes a finite number of trajectories and is bound to miss those rare events. It thus fails to reproduce the correct mean-square dynamics (under reasonable cost). A straightforward application of variance reduction techniques will typically not resolve the situation unless these methods force the rare, exploding trajectories to happen more frequently. Here we propose an appropriately tuned importance sampling technique based on Girsanov's theorem to deal with the rare event simulation. In addition further variance reduction techniques, such as multilevel Monte Carlo, can be applied to control the variance of the modified Monte Carlo estimators. As an illustrative example we discuss the numerical treatment of the stochastic heat equation with multiplicative noise and present simulation results.
    This is joint work with Markus Ableidinger and Andreas Thalhammer.

  • Erika Hausenblas (Montanuniversität Leoben) : The Stochastic Gray Scott system
    06.11.2017, 14:15, V5-148, Oberseminar Numerik
    Abstract: Reaction and diffusion of chemical species can produce a variety of patterns, reminiscent of those often seen in nature. The Gray Scott system is a coupled equation of reaction diffusion type, modelling these kind of patterns. Depending on the parameter, stripes, waves, cloud streets, or sand ripples may appear. These systems are the macroscopic model of microscopic dynamics. Here, in the derivation of the equation the random fluctuation of the molecules are neglected. Adding a stochastic noise, the inherit randomness of the microscopic behaviour is modelled. In particular, we add a time homogenous spatial Gaussian random field with given spectral measure.
    In the talk we present our main result about the stochastic Gray Scott system. In addition, we introduce and explain an algorithm for its numerical approximation by a Operator splitting method. Finally we present some examples illustrating the dynamical behaviour of the stochastic Gray Scott system.

  • Anna Khripunova-Balci (Vladimir State University) : On p(x)-connectedness of periodical measures
    30.10.2017, 14:15, V5-148, Oberseminar Numerik
    Abstract: We obtain the Gamma-convergence result for the sequence of integral functionals with non-standard growth conditions and measures. The key proberties that allows to pass to the limit in such problems is the so called p(x)-connectedness of measure. We also consider some connected problems or Sobolev-Orlich spaces with respect to measures.

  • Sebastian Schwarzacher (Bonn): Existence and discretisation of strong solutions to rate independent systems
    23.10.2017, 14:15, V5-148, Oberseminar Numerik
    Abstract: Rate-independent systems arise in a number of applications. Usually, weak solutions to such problems with potentially very low regularity are considered, requiring mathematical techniques capable of handling nonsmooth functions. The subject of this talk introduces a strategy which in contrast to existing approaches directly implies existence of Hölder-regular strong solutions for a class of rate-independent systems. Additionally higher regularity results are presented that guarantee the uniqueness of strong solutions. The proof proceeds via a time-discrete Rothe approximation and careful elliptic regularity estimates. Finally, a space-time discretization will be introduced of which we prove the convergence with a rate to the (strong) solution.
    The content of the talk is a joint work with F. Rindler (Warwick University) and E. Süli (Oxford University).

  • Janosch Rieger (Monash University Melbourne) : Applications of the solvability theorem for relaxed one-sided Lipschitz inclusions
    17.07.2017, 16:15, V5-148, Oberseminar Numerik
    Abstract: The solvability theorem guarantees the existence of a solution of a relaxed one-sided Lipschitz algebraic inclusion within a certain ball. This localisation can be used to characterise the boundary of the reachable set of a control system and, as a consequence, omit many redundant operations for its numerical approximation. It also induces a numerical scheme for the solution of the algebraic inclusion, provided the right-hand side is Lipschitz as well.

  • Tomasz Cieslak (Instytut Matematyczny Polskiej Akademii Nauk, Warschau) : Kaden's spiral and velocity of vortex sheet represented by the moments of its vorticity.
    03.07.2017, 16:15, V5-148, Oberseminar Numerik
    Abstract: I will review our recent common results with M.Szumanska, K. Oleszkiewicz and M. Preisner concerning the self-similar vortex sheets and their role in the 2d inviscid and incompressible flow. In particular I will show how to compute the velocity of Kaden's spiral and show that the energy is dissipated by such an object.

  • André Wilke (Bielefeld) : Analysis and numerics of total variation flow
    30.06.2017, 14:15, V5-148, AG Dynamische Systeme
    Abstract:

  • Franz Gmeineder (Oxford) : On the Neumann problem for variational integrals in BV
    19.06.2017, 15:00!, V2-105/115, Oberseminar Numerik
    Abstract: In this talk I give an overview of old and new results regarding the solvability of variational problems of linear growth, actually to be dealt with in the space BV of functions of bounded variation, in Sobolev spaces. Contrasting the rather restrictive results available in the Dirichlet case, we shall focus on the variational formulation of the Neumann problem on BV which allows for Sobolev solutions even in presence of high degeneracy of the integrands' ellipticity.
    This is joint work with L. Beck (Augsburg) and M. Bulicek (Prague).

  • Stefanie Hittmeyer (Auckland) : The geometry of blenders in a three-dimensional Hénon-like family
    19.06.2017, 16:15, , Oberseminar Numerik
    Abstract: Blenders are a geometric tool to construct complicated dynamics in diffeomorphisms of dimension at least three and vector fields of dimension at least four. They admit invariant manifolds that behave like geometric objects which have dimensions higher than expected from the manifolds themselves. We consider an explicit family of three-dimensional Hénon-like maps that exhibit blenders in a specific regime in parameter space. Using advanced numerical techniques we compute stable and unstable manifolds in this system, enabling us to show one of the first numerical pictures of the geometry of blenders. We furthermore present numerical evidence suggesting that the regime of existence of the blenders extends to a larger region in parameter space.
    This talk is based on joint work with Bernd Krauskopf, Hinke Osinga and Katsutoshi Shinohara.

  • Erwan Faou (Rennes) : On the long time stability of travelling wave for the discrete nonlinear Schrödinger equations
    09.06.2017, 14:15, , Oberseminar Numerik
    Abstract: I will discuss the possible existence of travelling wave solutions for discrete nonlinear Schrödinger equations on a grid. I will show the influence of the nonlinearity in this problem and give some partial results for the long time stability. This is a joint work with Dario Bambusi, Joackim Bernier, Benoît Grébert and Alberto Maspero.

  • Dominic Breit (University of Edinburgh) : Stationaly Solutions to the compressible Navier-Stokes system driven by stochastic Forces
    22.05.2017, 16:15, , Oberseminar Numerik
    Abstract: We study the long-time behavior of solutions to a stochastically driven Navier-Stokes system describing the motion of a compressible viscous fluid driven by a temporal multiplicative white noise perturbation. The existence of stationary solutions is established in the framework of Lebesgue-Sobolev spaces pertinent to the class of weak martingale solutions. The methods are based on new global-in-time estimates and a combination of deterministic and stochastic compactness arguments. In contrast with the deterministic case, where related results were obtained only under rather restrictive constitutive assumptions for the pressure, the stochastic case is tractable in the full range of constitutive relations allowed by the available existence theory. This can be seen as a kind of the noise on the global-in-time solutions.

  • Noel Walkington (Carnegie Mellon University, Pittsburgh) : Numerical Approximation of Multiphase Flows in Porous Media
    19.05.2017, 14:15, V5-148, AG Dynamische Systeme
    Abstract: This talk will review structural properties of the equations used to model geophysical flows which involve multiple components undergoing phase transitions. Simulations of these problems only model the gross properties of these flows since a precise description of the physical system is neither available nor computationally tractable. In this context mathematics provides an essential foundation to facilitate the integration of phenomenology and physical intuition to develop robust numerical schemes that inherit essential.

  • Sebastian Schwarzacher (Prag) : On compressible fluids interacting with a linear-elastic shell
    15.05.2017, 16:15, , Oberseminar Numerik
    Abstract: We study the Navier--Stokes equations governing the motion of an isentropic compressible fluid in three dimensions interacting with a flexible shell. The latter one constitutes a moving part of the boundary of the physical domain. Its deformation is modeled by a linearized version of Koiter's elastic energy. We discuss the existence of weak solutions to the corresponding system of PDEs provided the adiabatic exponent satisfies \(\gamma>\frac{12}{7}\) \(\gamma>1\) in two dimensions). The solution exists until the moving boundary approaches a self-intersection. This provides a compressible counterpart of the results in [D. Lengeler, M. Ruzicka, Weak Solutions for an Incompressible Newtonian Fluid Interacting with a Koiter Type Shell. Arch. Ration. Mech. Anal. 211 (2014), no. 1, 205--255] on incompressible Navier--Stokes equations.
    It is a joint work with D. Breit (Heriot-Watt Univ. Edinburgh).

  • Tsiry Randrianasolo (Montanuniversität Leoben) : Time-Discretization scheme of stochastic 2-D Navier-Stokes Equations by a Penalty-Projection method
    08.05.2017, 16:15, , Oberseminar Numerik
    Abstract: A time-discretization of the stochastic incompressible Navier-Stokes problem by penalty method is analyzed. Our work concerns the nonlinear term which in the stochastic framework prevents from using a Gronwall argument. Moreover, the approximate solution is slightly compressible and therefore, the nonlinear does not satisfy the additional orthogonal property which usually in two- dimension and with a periodic boundary condition allows to get some useful estimates. To tackle these issues we use the classical decomposition of the solution into an Ornstein-Uhlenbeck process and a solution of a deterministic Navier-Stokes equation depending on a stochastic process. The first part is stochastic but linear while the second one is nonlinear but deterministic. Both sub problems are still approximated with a numerical scheme based on penalty method. Error estimates for both of them are derived, combined, and eventually arrive at a convergence in probability with order 1/4 of the main algorithm towards the initial problem for the pair of variables velocity and pressure. The strong convergence of the scheme is achieved by means of the Bayes formula.

  • Christian Döding (Bielefeld) : Traveling Oscillating Fronts in Parabolic Evolution Equations"
    03.02.2017, 14:15, , AG Dynamische Systeme
    Abstract: We consider complex-valued parabolic evolution equations in one space dimension that are equivariant under spatial translation and, in addition, admit a symmetry under complex phase-shift. A major example is the complex quintic Ginzburg-Landau equation. In this talk we are interested in traveling oscillating front solutions. The solutions admit a fixed profile, which travels in space and oscillates in the time evolution, by multiplication with a time-dependent rotational term. Besides, the profile converge to the zero steady state on the one side and to a complex-valued but nonzero steady state on the other. The stability behavior, especially the nonlinear stability, of the solutions is almost unknown. I will give an introduction into the topic and will show how to compute such solutions numerically as heteroclinic orbits of a three dimensional dynamical system. Further, I will derive the equivalent real-valued system, state the corresponding Cauchy-problem and give a first spectral analysis of the occurring operator, which is relevant for studying the nonlinear stability of these solutions.

  • H.J. Schroll (University of Southern Denmark, Odense) : Computational Modeling of Fluorescence Loss in Photobleaching
    16.01.2017, 14:15, V5-148, Oberseminar Numerik
    Abstract: A quantitative analysis of intracellular transport processes is essential for the diagnosis and improved treatment of diseases like Alzheimer, Parkinson, lysosomal storage disorders and arteriosclerosis. Fluorescence loss in photobleaching (FLIP) is a modern microscopy method for visualization of transport processes in living cells. Although FLIP is widespread, only few studies attempt yo derive quantitative models of the transport processes underlying observed FLIP image sequences. This paper presents the simulation of FLIP sequences based on a calibrated reaction--diffusion system defined on segmented cell images. The PDE model is conveniently implemented in the automated Finite Element software package FEniCS. By the use of a discontinuous Galerkin method, the computational complexity is drastically reduced compared to continuous Galerkin methods. Using this approach on green fluorescent protein (GFP), we are able to determine its intracellular diffusion constant, strength of localized hindrance to diffusion as well as the permeability of the nuclear membrane for GFP passage, directly from the FLIP image series. This sets the stage towards detailed description of the transport dynamics underlying observed FLIP data in other applications.

  • Jens Rottmann-Matthes (Karlsruhe) : An IMEX-RK scheme for capturing similarity solutions in multi-dimensional Burger's equation
    12.12.2016, 14:15, X-E0-002 !!, Oberseminar Numerik
    Abstract: The topic of the talk are similarity solutions occuring in multi-dimensional Burger's equation. In the first part we present a simple derivation of the symmetries that appear in a family of general Burgers' equation in \(d\)-space dimensions. We use these symmetries to derive an equivalent partial differential algebraic equation (freezing system). In the second part we concentrate on the numerical approximation of this PDAE. We introduce a new and easily implementable numerical scheme, based on an IMEX-Runge-Kutta approach for a method of lines (semi-)discretization of the freezing PDAE. We prove second order convergence for the time discretization at smooth solutions. Numerical experiments show that our method enables us to do long time simulations and obtain good approximations of similarity solutions to the multi-dimensional Burgers' equation by direct forward simulation. The method also allows us without further effort to observe meta-stable behavior near N-wave-like patterns. Moreover, the experiments give numerical evidence that the method is indeed second order convergent for all positive values of viscosity. Because the multi-dimensional Burgers' equation can be considered as a PDE with a parabolic or hyperbolic dominating part for large, resp. very small viscosities, our findings suggest that the scheme is indeed suitable for the discretization of  the freezing PDAE for general coupled hyperbolic-parabolic PDEs.

  • Christian Meyer (TU Dortmund) : Optimal Control of Variational Inequalities
    21.11.2016, 14:15, V5-148, Oberseminar Numerik
    Abstract: Many applications are modeled by variational inequalities (VIs), in particular in computational mechanics. Classical examples are elastoplastic deformations, contact problems, or damage evolution. The solution mappings associated with these models are in general not Gâteaux-differentiable. Therefore, standard techniques in optimal control based on the control-to-state mapping are not applicable. Remedies are regularization and relaxation approaches as well as techniques that employ the limited differentiability properties of the solution map associated with the respective VI. We will present several of these approaches from a theoretic as well as numerical perspective.

  • D. Otten (Universität Bielefeld) : Fredholm Properties and \(L^P\)-Spectra of Localized Rotating Waves in Parabolic Systems
    18.11.2016, 14:15, V5-148,
    Abstract: Rotating waves are special solutions of reaction-diffusion systems which rotate at constant velocity while maintaining their shape. Nonlinear stability results for such waves are usually based on spatial behavior of the wave profile and on spectral properties of the linearization. The linearization, obtained by linearizing the co-rotating frame at the wave profile, turns out to be an additive variable coefficient perturbation of a complex-valued Ornstein-Uhlenbeck operator. In this talk we first present a short review about previous results on exponential decay of rotating waves. We then investigate Fredholm properties of the linearization, derive the Fredholm alternative and show under suitable assumptions that eigenfunctions and their adjoints decay exponentially in space. We then provide different techniques to derive certain subsets of the spectrum of the linearization. The main idea is to reduce the eigenvalue problem of the linearized operator to a finite-dimensional one. For this purpose, we first derive the dispersion set, which is affected by the far-field behavior of the wave, and show that it belongs to the essential \(L^P\)-spectrum. We then derive the symmetry set, which is induced by the underlying group symmetries, and show that it belongs to the point \(L^P\)-spectrum. From Fredholm properties we deduce exponential decay of the associated eigenfunctions and their adjoints. Finally, we present numerical results for spinning solitons that appear in the cubic-quintic complex Ginzburg-Landau equation.

  • Dimitra Antonopoulou (University of Chester) : Existence and Regularity of Solution for a stochastic Cahn-Hilliard/Allen-Cahn Equation with unbounded Noise Diffusion
    07.11.2016, 14:15, V5-148, Oberseminar Numerik
    Abstract: The Cahn-Hilliard/Allen-Cahn equation with noise is a simplified mean field model of stochastic microscopic dynamics associated with adsorption and desorption-spin flip mechanisms in the context of surface processes. For such an equation we consider a multiplicative space-time white noise with diffusion coefficient of linear growth. Applying technics from semigroup theory, we prove local existence and uniqueness in dimensions d = 1, 2, 3. Moreover, when the diffusion coefficient satisfies a sub--linear growth condition of order $\alpha$ bounded by 1/3, which is the inverse of the polynomial order of the nonlinearity used, we prove for d=1 global existence of solution. Path regularity of stochastic solution, depending on that of the initial condition, is obtained a.s. up to the explosion time. The path regularity is identical to that proved for the stochastic Cahn--Hilliard equation in the case of bounded noise diffusion. Our results are also valid for the stochastic Cahn--Hilliard equation with unbounded noise diffusion, for which previous results were established only in the framework of a bounded diffusion coefficient. As expected from the theory of parabolic operators the bi--Laplacian operator seems to be dominant in the combined model.
    Joint work with G. Karali and A. Millet.

  • W.--J. Beyn (Universität Bielefeld) : Stability and Computation of waves in second order evolution equations
    24.10.2016, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we consider traveling waves of a semilinear damped wave equation. We show how the freezing method generalizes from first to second order evolution equations by transforming the original PDE into a partial differential algebraic equation (PDAE). Solving a Cauchy problem via the PDAE generates a comoving frame in which the solution becomes stationary, and an additional variable which converges to the speed of the wave, provided the original wave has suitable stability properties. A rigorous theory of this effect is presented in one space dimension, building on recent nonlinear stability results for waves in first order hyperbolic systems. Numerical examples demonstrate the applicability of the method, and generalizations to rotating patterns in several space dimensions indicate its scope.

  • Barnabas M. Garay (Faculty for Information Technology and Bionics, Pazmany Peter Catholic University, Budapest) : On metastable rotating waves in Chua-Yang ring networks
    19.08.2016, 14:15, V5-148, AG Dynamische Systeme
    Abstract: The topic of the this talk is the phenomenon of long-transient oscillations observed experimentally in a Chua-Yang electrical circuit. Such periodic oscillations seem to be asymptotically stable for several seconds --- a time almost as long as eternity in electrical engineering. In a piecewise linear ODE system with rotational symmetry modelling a circular cellular neural network array with a saturated, three-segment piecewise linear activation and two-sided, not-necessarily cooperative interconnections, exponentially small lower and exponentially small upper estimates for the critical Instability Gap are presented.

    M.Forti, B.M.Garay, M.Koller, L.Pancioni, Long transient oscillations in a class of cooperative cellular neural networks, Int. J. Circuit Theory Applications} 43(2015), 635.
    M.DiMarco, M.Forti, B.M.Garay, Koller, L.Pancioni, Floquet multipliers of a metastable rotating wave in a Chua-Yang ring network, J. Math. Anal. Appl. 434(2016), 798-836.

  • Thorsten Hüls: A contour algorithm for computing stable fiber bundles of nonautonomous, noninvertible maps
    06.06.2016, 16:15, V5-148, Oberseminar Numerik
    Abstract: Stable fiber bundles are the nonautonomous analog of stable manifolds and these objects provide valuable information on the underlying dynamics. We propose an algorithm for their approximation that is based on computing zero contours of a particular operator. The resulting program applies to a wide class of models, including noninvertible and nonautonomous discrete time systems. Precise error estimates are provided and fiber bundles are computed for several examples. Finally, we apply the contour algorithm to (non)autonomous ODEs. For the famous three-dimensional Lorenz system, we calculate several approximations of the two-dimensional Lorenz manifold.

  • Matthew Salewski (TU Berlin) : Equivariance and reduced-order modelling
    27.05.2016, 14:15, V5-148, AG Dynamische Systeme
    Abstract: The construction of reduced-order models from a dynamical system can be enhanced when one uses properties of the system, such as the equivariance of the system under the action of a Lie group. This allows the dynamics to be reduced to a subspace where the action of the group has been removed. This effect can be advantageous when applied to systems of transport-dominated phenomena, for example a moving localized pulse or front which generally pose problems for accurate modeling. Here, i discuss a protocol for constructing reduced-order models using equivariance, and demonstrate this protocol with simple systems exhibiting transport-dominated phenomena. In addition, I will comment on systems whose equivariance is not explicitly clear and show some approaches used to deal with this when constructing a model.

  • Arnd Scheel (Minnesota): Defects in Striped Phases
    09.05.2016, 16:15, V5-148, Oberseminar Numerik
    Abstract: Many nonlinear systems admit families of striped solutions, which are periodic in one spatial variable. A prototypical system is the Swift--Hohenberg equation with cubic nonlinearity. I will discuss attempts to describe patterns that deviate from exact spatial periodicity due to the presence of boundary conditions, inhomogeneities, or 'self--organized' defects.

  • Markus Ableidinger (JUK Linz): Structure preserving splitting integrators for SDEs
    30.03.2016, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we will discuss stochastic differential equations where the solution trajectories are governed by geometric structures as, e.g. energy preservation or dissipation. An efficient strategy for constructing structure preserving integrators is to split the SDE into subsystems which inherit the geometric structure and build a numerical integrator by composition of the exact flows of the subsystems. We apply this approach on SDEs arising in micromagnetism (stochastic Landau-Lifshitz-Gilbert equation) and neuroscience (stochastic Jansen and Rit Neural Mass Model).

  • Janosch Rieger (Imperial College London): Generalized Convexity and Set Computation
    18.03.2016, 14:15, V5-148, Oberseminar Numerik
    Abstract: Generalized convexity has mainly been studied in optimization theory with a focus on generalized convex functions. In this talk, I will give a brief introduction to convex sets from a support function point of view before discussing generalized convex sets and their use for set representation and computation. Some of the content will be work in progress.

  • Stefan Liebscher (Technology Consulting München): The Tumbling Universe: Cosmological Models in the Big-Bang Limit
    22.01.2016, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Cosmological models are solutions of the Einstein field equations. We are interested in the alpha-limit dynamics describing the early universe.
    We will discuss possible model reductions facilitated by symmetry assumptions. Focus is on Bianchi cosmologies. They yield spatially homogeneous, anisotropic solutions of the Einstein field equations.
    The (backward) attractor of the Bianchi system is composed of the Kasner circle of equilibria and attached heteroclinic connections. The Kasner equilibria correspond to self-similar cosmologies. General solutions in the Big-bang limit follow heteroclinic chains of the attractor and describe universes which tumble between different self-similar cosmologies.

  • Hari Shankar Mahato (Universität Erlangen-Nürnberg) : Homogenization of Some Two-scale Models in Porous Media
    11.01.2016, 16:15, V5-148, Oberseminar Numerik
    Abstract: A porous medium (concrete, soil, rocks, water reservoir, e.g.) is a multi-scale medium where the heterogeneities present in the medium are characterised by the micro scale and the global behaviours of the medium are observed by the macro scale. The upscaling from the micro scale to the macro scale can be done via averaging methods. In this talk, we consider two models: M1 and M2. In M1 diffusion and reaction of mobile chemical species are considered in the pore space of a porous medium. The reactions amongst the species are modelled via mass action kinetics and the modelling leads to a system of multi-species diffusion-reaction equations (coupled semi-linear partial differential equations) at the micro scale where the highly nonlinear reaction rate terms are present at the right hand sides of the system of PDEs, cf. [2]. In model M2, diffusion, advection and reaction of two different types of mobile species (type I and type II) are considered at the micro scale. The type II species are supplied via dissolution process due to the presence of immobile species on the surface of the solid parts. The presence of both mobile and the immobile species make the model complex and the modelling yields a system of semi-linear partial differential equations coupled with ordinary differential equations with jump discontinuity. For both M1 and M2, the existence of a unique positive global weak solution is shown with the help of a Lyapunov functional, Schaefer's fixed point theorem and some regularisation technique, cf. [2, 3]. Finally with the help of two-scale convergence and periodic unfolding, M1 and M2 are upscaled from the micro scale to the macro scale, e.g. [1, 3]. Some numerical simulations will also be shown in this talk, however for the purpose of illustration, we restrict ourselves to some relatively simple 2- dimensional situations.

    References:
    [1] G. Allaire, Homogenization and two scale convergence, SIAM Journal of Mathematical Analysis, 23(6), 1482-1518, 1992.

    [2] H.S. Mahato and M. Böhm, Global existence and uniqueness for a system of nonlinear multi-species diffusion-reaction equations in an H1,p setting, Journal of Applied Analysis and Computation, 3(4), 357-376, 2013.

    [3] H.S. Mahato and M. Böhm, An existence result for a system of coupled semilinear diffusion-reaction equations with flux boundary conditions, European Journal of Applied Mathematics, 2014.

  • Péter Koltai (FU Berlin): Coherent Families: Spectral Theory for Transfer Operators in Continuous Time
    11.12.2015, 14:15, V5-148, AG Dynamische Systeme
    Abstract: The decomposition of the state space of a dynamical system into metastable or almost-invariant sets is important for understanding macroscopic behavior. This concept is well-understood for autonomous dynamical systems, and has recently been generalized to non-autonomous systems via the notion of coherent sets. We elaborate here on the theory of coherent sets in continuous time for periodically-driven flows and describe a numerical method to find families of coherent sets without trajectory integration.

  • David Hilditch (Universität Jena): The formulation, theory and practice of Numerical Relativity
    10.12.2015, 10:15, V4-106, Oberseminar Numerik
    Abstract: I will give an introduction to the basic subject matter of Numerical Relativity. Starting with simple toy problems, I will discuss the formulation of General Relativity as an initial value problem and the requirement of well-posedness of the resulting PDE problem. I will summarize standard numerical methods and outline the major topics of the field. Finally I will discuss my own work on collapsing gravitational waves and on the relationship between gauge and coordinate freedom.

  • Jochen Röndigs (Uni Bielefeld): Foundations for General Relativity
    07.12.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: With a brief summary of Special Relativity (SR) we introduce the corresponding mathematical model of flat spacetime, which is called a Minkowski space, characterised by a special, generalised scalar product (the Minkowski metric). A short analysis of the spacetime structure, that is the metric and isometries (Lorentz transformations), is presented including some of the major consequences of SR. As a preparation for General Relativity with curved spacetime, which is modeled as a manifold over a Minkowski space, the basic concepts for differential geometry and manifolds are introduced. The final goal is to be ready for the Einstein field equations and the talk about Numerical Relativity on Thursday.

  • Bernhard Lani-Wayda (Uni Gießen): Chaotic motion in delay equations
    30.11.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: In delay equations, such as \(x'(t) = - \mu x(t) + f(x(t-1))\), apparently chaotic behavior was frequently observed in numerical simulations since the 1970s. Analytical proofs are, generally speaking, still out of reach, but exist for some examples. The talk presents some of these examples, the relevant geometric-topological structures and the techniques of proof, along with some open problems.

  • Nils Hartmann (Uni Bielefeld): Umkehrpunkte periodischer Lösungen zeitkontinuierlicher autonomer Systeme
    27.11.2015, 14:15, V5-148, AG Dynamische Systeme
    Abstract: In diesen Vortrag behandeln wir ausgehend von einer eindeutigen periodischen Lösung einer autonomen Differentialgleichung bei festem Parameter die Lösungsfortsetzung im Phasenraum mit variablem Parameter. Im Anschluss werden wir eine geeignete Testfunktion für quadratische Umkehrpunkte definieren und je nach verbliebener Zeit deren Regularität beweisen.

  • Christian Kahle (Uni Hamburg): Simulation and Control of two phase fluids using a diffuse-interface model
    16.11.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: The simulation of multiphase fluids has attained growing interest in the last decades. While for one phase flow with the Navier--Stokes system the basic model is well understood for multiphase system additional challenges arise by the necessity to track the transition zones or interfaces between different fluid components. Methods to track these zones split in two general concepts, namely representing the interface as a lower dimensional manifold (sharp interface) and tracking its evolution due to the outer velocity field, or introducing a phase field function or order parameter for the description of the distribution of the phases. A phase field is a smooth indicator function with distinct values in the two phases that yields a smooth transition between these values over a small length scale where the interface is located. In this talk a diffuse interface model is discussed that is consistent with thermodynamics. Also a discrete concept that is able to preserve this feature in the discrete setting is provided. Based on this stable discrete concept optimal control of two phase fluids is introduced and analyzed.

  • Thomas Dunst (Uni Tübingen): The Forward-Backward Stochastic Heat Equation: Numerical Analysis and Simulation
    26.10.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: I report on recent results to numerically approximate the forward-backward stochastic heat equation. For this purpose, I start with showing strong convergence with optimal rates for a spatial discretization of the backward stochastic heat equation, which is then extended to strong optimal rates for the forward-backward stochastic heat equation from optimal stochastic control. A full discretization based on the implicit Euler method for a temporal discretization, and a least squares Monte-Carlo method are then proposed and simulation results are reported. This talk is based on a joint work with Andreas Prohl (Uni Tübingen).

  • Raphael Kruse (TU Berlin): Numerical approximation of SDEs under a one-sided Lipschitz condition
    05.10.2015, 14:15!!, V2-200, Oberseminar Numerik
    Abstract: In this talk we present some new results on the numerical approximation of stochastic differential equations, which satisfy the so called global monotonicity condition. In particular, we study the mean-square error of convergence of the backward Euler method and the BDF2-Maruyama scheme. The proof relies on new stability results and a priori estimates of the numerical schemes.

  • Nils Hartmann: Periodische Lösungen zeitkontinuierlicher autonomer Systeme
    17.07.2015, 15:15, V5-148, AG Dynamische Systeme
    Abstract: In dem Vortag wird zuerst die Existenz und Eindeutigkeit periodischer Lösungen in autonomen zeitkontinuierlichen Systemen behandelt. Danach werden mit Hilfe der Floquet Theorie hinreichende und notwendige Bedingungen für die orbitale Stabilität periodischer Orbits diskutiert. Anschließend befassen wir uns mit der Theorie der numerischen Berechnung von periodischen Lösungen.

  • Seung-Yeal Ha (Seoul): Synthesis of synchronization and flocking: From Winfree to Cucker-Smale
    13.07.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: Collective behaviors of complex systems are often observed in our nature, i.e., flocking of birds, swarming of fishes and synchronization of pacemaker cells etc. In this talk, we present recent progress for the unification of flocking and synchronization in one framework. For this, we will discuss several mathematical models and how these models can be studied in the same methodology.

  • Christian Vieth: Konfidenzellipsoide in stochastischen Differentialgleichungen und die Lyapunov Gleichung
    10.07.2015, 15:15, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten die Lyapunov Gleichung \[ AY+YA^T=-BB^T,\] die bei bei der Berechnung von Konfidenzellipsoiden stochastisch metastabiler Gleichgewichte auftritt. Ziel ist es, Lösbarkeit und Lösungsdarstellungen sowie numerische Verfahren vorzustellen.

  • Tatjana Stykel (Universität Augsburg): Model reduction of linear and nonlinear magneto-quasistatic problems
    03.07.2015, 14:15, V5-148, Oberseminar Numerik

  • Christina Göpfert: An Overview of Topological Entropy and Metric Entropy
    19.06.2015, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Topological entropy is an invariant under topological conjugacy. The corresponding notion in ergodic theory is the metric entropy, which is invariant under conjugacy in the ergodic sense. The two are connected by the variation principle. An application of these concepts is an algorithm for computing rigorous upper bounds for topological entropy by Froyland, Junge and Ochs. During the talk, we will discuss the aforementioned concepts and explore how they relate.

  • Amy Novick-Cohen (Technion, Haifa) : Geometric interfacial motions: coupling surface diffusion and mean curvature motion
    15.06.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: Mean curvature motion as well as surface diffusion constitute geometric interfacial motions which have received considerable attention. However in many applications a complex combination of coupled surfaces appear whose evolution may be described by coupling these two types of motion. In my lecture, a variety of physical problems will be described which may be reasonably modeled by such motions. While some these problems appear to require an anisotropic formulation, often an isotropic formulation is helpful to consider. A panoply of analytic and numerical results will be presented, in addition to some supporting experimental evidence.

  • Christian Döding (Universität Bielefeld): Abschätzungen des Quadraturfehlers für Konturintegrale und ihre Anwendung auf die inverse Laplacetransformation
    01.06.2015, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Zur numerischen Lösung von parabolischen Gleichungen wurden exponentielle Integratoren vorgestellt, die sich durch inverse Laplacetransformation auswerten lassen. Diese inversen Laplacetransformationen sind Konturintegrale, welche durch Quadraturformeln approximiert werden. Ziel des Vortrages ist es für den Quadraturfehler dieser Approximationen Abschätzungen zu beweisen, die die Eigenschaften des Integrationsweges, welcher als Hyperbel gewählt werden kann, und die sektorielle Eigenschaft des Integranden ausnutzen.

  • Malte Braack (M. Quaas, B. Tews) (Universität Kiel): Fishing strategies as an optimal control problem in multi dimensions
    29.05.2015, 14:15, V5-148, Oberseminar Numerik
    Abstract: Marine fisheries are very important to the economy and livelihood of coastal communities, providing food security and job opportunities. The preservation of long-term prosperity and sustainability of marine fisheries is of political and social significance as well as economical and ecological importance. Due to new technologies allowing to catch more fish, various fish stocks like tuna, swordfish, shark, cod, halibut, etc. have declined by up to 90% in the last decades. Therefore, some states introduced policy instruments including landing fees, total allowable catches (TAC's) and marine protect areas (MPA's). In this context, important social and economical questions arise about the optimal amount of TAC's as well as the design of those MPA's: What is the optimal size and location of MPA's with regard to suficient recovery of the fish stock as well as suficient amount of fisheries yield.
    To address to these questions mathematically, the fishing strategy can be formulated as an optimal control problem. The fish stock dynamics are modeled by a time-dependent, non-linear PDE including reproduction and growth rate. The space-time distributed control describes the fishing intensity and is assumed to be bilinear with the biomass. The cost functional takes into account the benefit of the harvest, fishing costs and the fish stock density at final time which guarantees sustainability. It turns out that the optimization problem complemented with additional control constraints results in a non-standard and non-linear optimal control problem. This talk is dedicated to the analysis of this problem in terms of solvability and optimality conditions. We also show first numerical examples.

  • Misha Neklyudov (University of Pisa) : New type of homogenisation problem for stochastic parabolic equations
    29.04.2015, 16:00, D5-153,
    Abstract: We will show that the solution of 1D stochastic parabolic equation with additive noise converges to a diffusion process independent upon space variable when we rescale noise at the extremum points of the process. We will discuss open problems and suggest future directions of research. The talk is based on a joint work in progress with Ben Goldys.

  • Christian Döding : Realisierung exponentieller Integratoren mittels Laplacetransformation
    06.02.2015, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Es werden parabolische Differentialgleichungen betrachtet, die sich als gewöhnliche Differentialgleichungen in einem Banachraum abstrakt schreiben lassen. Da der auftretende Differentialoperator sektoriell ist, lassen sich spezielle numerische Verfahren zum Lösen dieser Gleichungen definieren - die sogenannten exponentiellen Integratoren. Zur Realisierung dieser Verfahren ist es nötig Funktionen exponentieller Form auf Operatorebene auszuwerten. Aufgrund der Unbeschränktheit des Differentialoperators scheitert der Ansatz über Potenzreihen. Vorgestellt wird eine Konturmethode basierend auf der Laplacetransformation, welche einen Ausweg aus diesem Problem aufzeigt.

  • Lukasz Targas: Sudoku ist ein NP-vollständiges Problem
    02.02.2015, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Wir werden die Klasse der NP-vollständigen Probleme definieren und zeigen, dass das Lösen eines Sudoku-Rätsels zu dieser Klasse gehört. Dafür werden wir einige graphentheoretische und kombinatorische Probleme (SAT, 3SAT, 1in3SAT, Triangulation 3-färbbarer Graphen, Vervollständigung lateinischer Quadrate, Lösung von Sudoku-Rätsel) ineinander polynomiell transformieren. Die Ideen der Transformationen werden an zahlreichen Beispielen motiviert.

  • Alina Girod: Erste Einführung in die Theorie zeit-endlicher dynamischer Systeme
    30.01.2015, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Die Definitionen für Hyperbolizität, den stabilen und instabilen Unterraum, sowie für die stabile und instabile Mannigfaltigkeit eines zeit-unendlichen dynamischen Systems werden wir auf zeit-endliche Systeme übertragen. Dabei werden wir feststellen, dass hyperbolische zeit-endliche Systeme keine eindeutigen Projektoren besitzen. Daher können wir nur stabile und instabile Kegel definieren, anstatt stabiler und instabiler Unterräume. Für diese Kegel leiten wir explizite Darstellungen her. Anschließend werden wir diese in einem Beispiel betrachten.

  • Evamaria Ruß (Univ. Klagenfurt): Dichotomy Spectrum in Infinite Dimensions
    19.01.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: The dichotomy spectrum (also known as Sacker-Sell or dynamical spectrum) is a crucial spectral notion in the theory of dynamical systems. In this talk we study the dichotomy spectrum in infinite dimensions. In general we cannot expect a nice structure of the dichotomy spectrum like in the finite dimensional case, but compactness properties of the transition operator provide a more regular spectrum. Finally, we consider applications.

  • Jens Rademacher (Uni Bremen): Pattern formation in simple spintronic device models with aligned fields
    12.01.2015, 16:15, V5-148, Oberseminar Numerik
    Abstract: The self-organized emergence of spatio-temporal patterns is a ubiquitous phenomenon in nonlinear processes on large homogeneous domains. In this talk a class of Landau-Lifshitz-Gilbert-Slonczewski equations is studied from this viewpoint, highlighting various aspects of the theory. The model describes magnetization dynamics in the presence of an applied field and a spin polarized current. Here we consider the case of axial symmetry and focus on the analysis of coherent structure solutions that occur due to the symmetry. This is joint work with Christof Melcher (RWTH).

  • Robert Haller-Dintelmann (TU Darmstadt): Generalized Ornstein-Uhlenbeck operators in \(L^p\) spaces on domains
    15.12.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: We consider the Ornstein-Uhlenbeck operators \[ A u (x) = \text{div} Q \nabla u(x) + Bx \cdot \nabla u(x) \] with suitable matrices \(Q\), \(B\) and a generalized version \[ A u(x) = \text{div} \mu(x) \nabla u(x) + b(x) \cdot \nabla u(x), \] where \(\mu\) is a bounded coeffiecient function and \(b\) is allowed to grow more or less linearly. We show that these operators, complemented with Dirichlet boundary conditions, are generators of consistent, positive, (quasi-)contractive \(C_0\)-semigroups on \(L^p(\Omega)\) for all \(1 \le p \lt \infty\) and for every domain \(\Omega \subseteq {\mathbb{R}}^d\). In order to do so, we use a generation result in \(L^2(\Omega)\) and derive kernel estimates for this semigroup. In the special case of an exterior domain with sufficiently smooth boundary it is even possible to give a result on the location of the spectrum of Ornstein-Uhlenbeck opperators on domains.

  • Christian Vieth (Bielefeld): Deterministische Fortsetzung von Gleichgewichten und Konfidenzellipsoiden in stochastischen Differentialgleichungen
    12.12.2014, 14:15, V5-148, AG Dynamische Systeme

  • Fabian Wirth (Univ. Passau): Stabilisierbarkeit linearer zeitvarianter Systeme
    8.12.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: Wir betrachten lineare zeitvariante Kontrollsysteme in stetiger Zeit und untersuchen die Frage, unter welchen Bedingungen stabilisierende Rückkopplungen existieren. Im zeitinvarianten Fall ist dieses Problem seit langem geklärt. Kontrollierbarkeit ist äquivalent zu der Eigenschaft, dass beliebige Eigenwerte durch Rückkopplung vorgegeben werden können. Das System ist stabilisierbar, wenn der instabile Unterraum des freien Systems im kontrollierbaren Unterraum enthalten ist. Für zeitvariante Systeme werden die entsprechenden Fragestellungen feiner, schon weil die Stabilitätsbegriffe gleichmäßige exponentielle Stabilität, exponentielle Stabilität und asymptotische Stabilität auseinander fallen. Zur Charakterisierung der verschiedenen Stabilitätseigenschaften werden Bohl- und Lyapunovexponenten verwendet, und die Frage ist dann, welche Bohl- oder Lyapunovexponenten durch Rückkopplung erreichbar sind. Im Vortrag wird der Zusammenhang zwischen (gleichmäßiger) exponentieller Stabilisierbarkeit und (gleichmäßiger) Kontrollierbarkeit diskutiert und es werden Methoden aus der optimalen Steuerung vorgestellt, mit deren Hilfe die entsprechenden Aussagen bewiesen werden können. Diese Methoden liefern außerdem ein Kriterium für die Stabilisierbarkeit zeitvarianter Systeme.

  • Tomas Dohnal (Uni Dortmund):
    01.12.2014, 16:15, V5--148, Oberseminar Numerik
    Abstract: In periodic media, e.g., photonic crystals, the quest for moving localized pulses with profiles that are close to constant or periodic in time is interesting from a mathematical as well as an applied point of view. In optical computing such pulses would be versatile bit carriers. We seek them for frequencies in spectral gaps (so called band gaps) of the spatial operator and call them \textit{gap solitons}.
    Asymptotically near spectral edges gap solitons can be approximated as linear carrier waves modulated by slowly varying envelopes, which satisfy effective nonlinear amplitude equations. The carrier waves need to have a nonzero group velocity to guarantee movement of the gap soliton. Moving gap solitons have been previously studied only in structures with asymptotically small contrast of the periodicity because in finite contrast structures the group velocity of the corresponding carrier waves is generically zero. In 1D for perturbations of, so called, \textit{finite band periodic potentials} this is, however, violated and moving gap solitons are possible.
    Starting with the 1D peri odic nonlinear Schrödinger equation \[{\rm i}\partial_t u +\Delta u-V(x) u -\sigma |u|^2 u =0, \quad x\in \mathbb{R}, \] we present a derivation of the corresponding effective envelope equations and a technique to obtain localized solutions of these. We present numerical examples and discuss the current project on a rigorous justification of the effective equations.

  • Hannes Uecker (Univ. Oldenburg) : Generic Bifurcation of Nonlinear Bloch Waves from the Spectrum in the Gross-Pitaevskii Equation
    24.11.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: We rigorously analyze the bifurcation of so called nonlinear Bloch waves (NLBs) from the spectrum in the Gross-Pitaevskii (GP) equation with a periodic potential, in arbitrary space dimensions. These are solutions which can be expressed as finite sums of quasi-periodic functions, and which in a formal asymptotic expansion are obtained from solutions of the so-called algebraic coupled mode equations. Here we justify this expansion by proving the existence of NLBs and estimating the error of the formal asymptotics. The analysis is illustrated by numerical bifurcation diagrams, mostly in 2D, and we also illustrate some relations to other classes of solutions of the GP equation, in particular to so called out--of--gap solitons and truncated NLBs. Das verbindet sozusagen Analysis für wave-trains mit Illustration via pde2path.

  • Sören Bartels (Uni Freiburg): Finite element approximation of functions of bounded variation
    17.11.2014, 15:00!, U0-131!, Oberseminar Numerik
    Abstract: Various phenomena involving free boundaries such as damage or plasticity require the description of physical quantities with discontinuous functions. One approach to their mathematical modeling is based on the space of functions of bounded variation which includes functions that are discontinuous and may jump across lower dimensional subsets. Numerical methods for their approximate solution are often based on regularizations which typically lead to restrictive conditions on discretization parameters. We try to avoid such modifications and discuss the convergence of discretizations with different finite element spaces, the iterative solution of the resulting finite-dimensional nonlinear systems of equations, and adaptive mesh-refinement techniques based on rigorous a~posteriori error estimates for a model problem related to image processing. The application of the techniques to total variation flow, very singular diffusion processes, and segmentation problems will be addressed. Part of this talk is based on joint work with Ricardo H. Nochetto (University of Maryland, USA) and Abner J. Salgado (University of Maryland, USA).

  • Achim Schädle (Univ. Düsseldorf) : Transparent boundary conditions --- On the relationship between the pole condition, absorbing boundary conditions and perfectly matched layers
    10.11.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: Transparent (or exact or non-reflecting) boundary conditions are employed to truncate infinite computational domains. They are usually non-local and expensive to evaluate. In this talk approximate cheap boundary condition for the Schr"odinger, the Klein-Gordon and the Helmholtz equation are derived based on the pole condition.
    We show that for the simplest model problem, the Helmholtz equation on an infinite strip, a certain discretization of the pole condition can be interpreted both as a high order absorbing boundary condition and a perfectly matched layer, two other well known methods to approximate a transparent boundary condition.

  • Etienne Emmrich (TU Berlin) : The peridynamic model in nonlocal elasticity theory
    27.10.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: Peridynamics is a nonlocal continuum theory which avoids any spatial derivative. It is believed to be suited for the description of fracture and other material failure, and to model multiscale problems. In this talk, we introduce the peridynamic model and discuss several aspects of its mathematical analysis. We review recent results on the existence of solutions to the peridynamic equation of motion for a large class of nonlinear pairwise force functions modeling isotropic microelastic material. Our method of proof applies also to other nonlocal evolution equations.
    This is joint work with Dimitri Puhst (Berlin).

  • Stefanie Hittmeyer (University of Auckland) : Bifurcations of invariant sets in a map model of wild chaos
    24.10.2014, 15:00, V5-148, Oberseminar Numerik
    Abstract: We study a two-dimensional noninvertible map that has been introduced by Bamon, Kiwi and Rivera in 2006 as a model of wild Lorenz-like chaos. The map acts on the plane by opening up the critical point to a disk and wrapping the plane twice around it; points inside the disk have no preimage. The bounding critical circle and its images, together with the critical point and its preimages, form the so-called critical set. This set interacts with the stable and unstable sets of a saddle fixed point and other saddle invariant sets. Advanced numerical techniques enable us to study how these invariant sets change as the parameters are varied towards the wild chaotic regime. We find a consistent sequence of four types of bifurcations, which we present as a first attempt towards explaining the geometric nature of wild chaos. In a different parameter regime, the map acts as a perturbation of the complex quadratic family and admits (a generalised notion of) the Julia set as an additional invariant set. When parameters are varied, this set interacts with the other invariant sets, leading to the (dis)appearance of saddle points and chaotic attractors and to dramatic changes in the topology of the Julia set. In particular, we find generalised Julia sets in the form of Cantor bouquets, Cantor tangles and Cantor cheeses. Using two-parameter bifurcation diagrams, we obtain an indication on the size of the parameter region where wild chaos is conjectured to exist and reveal a self-similar bifurcation structure near the period-doubling route to chaos in the complex quadratic family.

  • Raphael Kruse (TU Berlin) : A new approach to the weak error analysis for SDEs with multiplicative noise
    23.06.2014, 16:15, V5-148, Oberseminar Numerik

  • Joseph N. Paez (TU Dresden): Mathematical Modelling and Experimental Study of Engineering Systems: Applications to Oil-Well Drilling.
    13.06.2014, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this presentation we will describe a number of research projects carried out at the Centre for Applied Dynamics Research (CADR), Aberdeen University (United Kingdom). The topics to be covered are: Drifting Oscillators, Impacting Systems, Drill-String Vibrations and Rotor Dynamics. For all these investigations, a particular problem related to the Oil and Gas Industry has been considered. A crucial step in this research is the construction of suitable mathematical models capable of reproducing quantitative- or qualitatively the dynamic behavior observed via experimental measurements. All the models in question involve piecewise-smooth ODEs. In addition, a detailed bifurcation analysis of the models is carried out, for which we use the software package TC-HAT, an Auto 97 toolbox for the numerical continuation of periodic orbits of non-smooth systems.

  • Alina Girod : Homoclinic trajectories in non-autonomous systems and their discretization
    06.06.2014, 14:15, V5-148, AG Dynamische Systeme
    Abstract: We consider a continuous time non-autonomous dynamical system having two hyperbolic bounded trajectories that converge towards each other. Applying a one-step-method with sufficiently small step size we get hyperbolic bounded trajectories of the discretized system. They lie in a small neighborhood of the original trajectories and are also homoclinic. For verifying our error estimates, we construct an example in continuous time with known homoclinic trajectories. An illustration of homoclinic dynamics can be achieved by computing stable and unstable fiber bundles. For this task, an algorithm of England, Krauskopf and Osinga is introduced that we generalize to the non-autonomous case.

  • Torsten Buschmann : Modellgleichungen für Chemotaxis
    30.05.2014, 14:15, V5-148, AG Dynamische Systeme

  • Michael Hinze (Univ. Hamburg): Simulation and model predictive control of two-phase flows with variable density
    19.05.2014, 14:15, T2-234, Oberseminar Numerik
    Abstract: We present a fully practical residual-based adaptive simulation framework for two-phase flows with variable densities governed by a Cahn-Hilliard Navier-Stokes model with double obstacle potential. In particular we present a new stable time integration scheme. Moreover, we consider wall parallel Dirichlet boundary control of the flow part to achieve a prescribed concentration field. We present a recipe how to construct the underlying controller and how to achieve his stabilizing properties.
    This is joint work with Harald Garcke, Michael Hintermüller and Christian Kahle.

  • Thorsten Hohage (Univ. Göttingen): Hardy Space Infinite Elements for Waves with Different signs of Group and Phase Velocities
    28.04.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: We consider time harmonic wave equations in cylindric waveguides with physical solutions for which the signs of group and phase velocities differ. In particular, we will consider a one-dimensional fourth order model problem and two-dimensional elastic waveguides for which this phenomenon occurs. Standard transparent boundary conditions, e.g. the Perfectly Matched Layers (PML) method select modes with positive phase velocity, whereas physical modes are characterized by positive group velocity. Hence these methods yield stable, but unphysical solutions for such problems. We derive an infinite element method for a physically correct discretization of such waveguide problems which is based on a Laplace transform in propagation direction. In the Laplace domain the space of transformed solutions can be separated into a sum of a space of incoming and a space of outgoing functions where both function spaces are curved Hardy spaces. The curved Hardy space is constructed such that it contains a simple and convenient Riesz basis with moderate condition numbers. Our method does not use a modal separation and works on an interval of frequencies. In particular, it is well-adapted for the computation of resonances. Numerical experiments exhibit super-algebraic convergence and moderate condition numbers.

  • Georgy Kitavtsev (Max-Planck-Institut Leipzig): Stable FEM discretizations for a certain class of lubrication, shallow water and Korteweg systems.
    10.02.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we discuss existence of weak solutions and corresponding stable FEM discretizations for a certain class of PDEs that include some known lubrication, shallow water and Korteweg systems. A common feature of these systems and at the same time a challenge for their consideration is that the viscosity terms degenerate as the solution for density/height approaches zero. As a related consequence to this fact it was observed that these systems dissipate besides a classical energy functional a so call Bresch and Desjardins entropy one which provides a higher regularity for the density/height solution. Regularized systems and their FEM discretization possessing the same dissipative properties as the original ones will be presented and analyzed.

  • Andreas Prohl (Univ. Tübingen): Strong convergence with rates for discretizations of SPDEs with non-Lipschitz drift
    06.02.2014, 14:15, V5-148, AG Dynamische Systeme
    Abstract: I discuss the convergence analysis for space-time discretizations of three nonlinear SPDE's: the stochastic Navier-Stokes equation, the stochastic Allen-Cahn equation, and the stochastic mean curvature flow of planar curves of graphs. Depending on the drift operator, optimal rates w.r.t. strong convergence are valid for errors on large subsets, or on the whole sample set.

  • Roland Schnaubelt (TU Karlsruhe): Splittingmethoden für Schrödingergleichungen mit singulären Potentialen
    22.01.2014, 16:15, V5-148, Oberseminar Numerik

  • Andre Schenke : Der Satz von Smale für nichtinvertierbare Systeme
    17.01.2014, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Der Satz von Smale impliziert eine chaotische Dynamik in der Nähe eines transversalen homoklinen Orbits, welcher von einem Diffeomorphismus erzeugt wird. Wir geben einen Beweis einer Version des Satzes von Smale im nichtinvertierbaren Fall. Grundlage hierfür ist eine Arbeit von Beyn, welche auf einer Idee von Palmer beruht. Wichtigstes Hilfsmittel ist eine nichtinvertierbare Version des Shadowing-Lemmas.

  • Misha Neklyudov (University of Sydney): Dynamics of nanomagnetic particle systems
    13.01.2014, 16:15, V5-148, Oberseminar Numerik
    Abstract: The dynamics of nanomagnetic particles is described by the stochastic Landau-Lifshitz-Gilbert (SLLG) equation.
    In the first part of the talk we will discuss the long time behaviour of the finite-dimensional SLLG equation. Firstly, we explain how statistical mechanics argument defines the form of the noise of the equation. Then we will consider different approximations of the equation such as structure preserving discretisation and penalisation approximation. We discuss the convergence of approximations andtheir consistency with the long time behaviour of the system.
    In the second part of the talk we will look at the infinite dimensional case. Firstly, we present a numerical scheme convergent to the solution of SLLG equation. Then we show some numerical results and discuss open problems, such as existence of invariant measure, existence of solution in the case of space-time white noise, etc. In particular we will explain why Krylov-Bogoliubov Theorem is not directly applicable to the proof of existence of invariant measure even in the case of coloured noise. In the end we will present certain transformation of SLLG equation which allows to represent the noise as the sum of additive noise and energy conservative noise.
    Computational examples will be reported to illustrate the theory.
    The talk is based on the recently published book (jointly with L. Banas, Z. Brzezniak, A. Prohl) and on the work in progress of the author.

  • Marc Winter : Taylor-Approximation invarianter Faserbündel (Teil 2)
    10.01.2014, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten eine nicht-autonome Differenzengleichung der Form \(x(n+1)=A(n)x(n)+F(x(n),n)\), \(n \in \mathbb{Z}\). Wir definieren die lokalen und globalen invarianten Faserbündel der Differenzengleichung als Analogon zu den Mannigfaltigkeiten autonomer Differenzengleichungen. Im ersten Vortrag haben wir untersucht, unter welchen Voraussetzungen diese Faserbündel existieren. Anschließend haben wir gesehen, wie wir diese Faserbündel mit Hilfe der Taylorentwicklung approximieren können. In diesem Vortrag werden wir die Ergebnisse einer Matlab-Implementation dieses Approximationsverfahrens betrachten. Wir werden das Verfahren auf eine spezielle Klasse von Funktionen anwenden, welche ein Polynom als Faserbündel besitzen, sowie auf die Hénon-Abbildung.

  • Elena Isaak (Bielefeld) : Numerical analysis of the balanced Milstein method
    13.12.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Balanced Milstein methods (BMM) have been proposed for solving numerically stochastic ordinary differential equations with large noise coefficients. In this talk we discuss consistency, bistability and convergence of the BMM. The main ingredient of the analysis is a stochastic version of Spijker's norm. We show that the order of consistency for the BMM in this norm is one, and we prove bistability which leads to two-sided estimates of the strong error of convergence.

  • Kathrin Glau (TU München): Kolmogorov backward equations for option pricing in Lévy models
    09.12.2013, 16:00, V5-148, Oberseminar Numerik
    Abstract: One major task mathematical finance sets itself is modeling, pricing and calibration of financial instruments. (Semi)martingale theory is used for modeling and derivative prices are written as conditional expectations. Typically, the latter are not available in closed form and, thus, computational methods become necessary. Essentially three approaches to compute the expectations are being used: Monte Carlo simulation, Fourier based valuation methods and the representation of prices as solutions of partial integro-differential equations (PIDEs). In this context we focus on Galerkin methods for solving PIDEs arising in Lévy models. We classify Lévy processes according to the solution spaces of the associated parabolic PIDEs and point out the role of the symbol. Furthermore, we derive Feynman-Kac representations of variational solutions. We discuss applications to option pricing and give an outlook on a Finite Element solver based on the symbol.

  • L´ubomír Banas (Bielefeld): Phase field models for multiphase flow: modelling, numerics and applications.
    02.12.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: Understanding and accurate prediction of multiphase multicomponent flows is of essential interest for a large number of scientific and engineering applications. Despite intensive past and present research efforts, it is still not clear how to accurately and efficiently simulate multiphase fluid flow for the full range of physical parameters and regimes such as, e.g., densities, viscosities, capillary relations, number of fluid phases, interface geometry, dynamic or static contact angles, etc. We review of a promising strategy for the modelling of incompressible multiphase flow based on the phase-field approach. We discuss advantages of the approach from the modelling and computational point of view. We also present a framework for multiscale flow simulations and discuss applications to multiphase flow in porous media.

  • Marian Slodicka (Gent): Inverse source problems in parabolic equations
    29.11.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Inverse coefficient and source problems for partial differential equations represent a well-known and established area of mathematical research in the last decades. They appear in various applied technologies (geophysics, optic, tomography, remote sensing, radar-location, etc.). Inverse source problems for evolutionary (parabolic, hyperbolic, Navier-Stokes) settings have been intensively studied by many authors. We study a problem of source identification from given data for the parabolic heat equation in several dimensions. The temperature \(u\), heat source \(F\) and the initial temperature distribution \(u_0(x)\) then satisfy \[\partial_tu + A u = F in\ \ \Omega\times (0,T),\] \[u(x,0) = u_0(x) for\ \ x\in \Omega\] along with appropriate boundary conditions. Here, \(A\) is a strongly elliptic, linear differential operator of second-order. The right-hand side \(F\) is assumed to be separable in both variables \(x\) and \(t\), i.e. \[F(x,t)=g(x)h(t).\] Two kinds of inverse problems will be addressed:
    -- reconstructing the source \(g(x)\) (when \(h(t)\) is given) from the additional information \(u(x,T) = \psi_T(x)\quad\mbox{for}\ \ x\in \Omega\)
    -- identification of the unknown function \(h(t)\) from additional data, assuming that \(g(x)\) is known. The unknown function \(h(t)\) is then recovered from a single point measurement \(u(y,t),\ t\in\ I\) at a given point \(y\in\overline\Omega\).

  • Ludwig Gauckler (TU Berlin): Mathematical and numerical analysis of Hamiltonian partial differential equations on long time intervals
    25.11.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: Qualitative properties of Hamiltonian partial differential equations on long time intervals are to be discussed in the talk, and the preservation of these properties by a numerical discretization will be studied. In the first part of the talk we will discuss for some numerical methods the long-time near-conservation of the energy, an important conserved quantity of these equations. In the second part of the talk we will study the long-time stability of plane wave solutions to the nonlinear Schrödinger equation, first for the exact solution and then for the numerical discretization of the equation by the popular split-step Fourier method.

  • Sebastian Paul : Ein endliches Kriterium zur Transversalität homokliner Orbits
    22.11.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Ziel des Vortrags ist ein numerisches Verfahren, mit dem wir homokline Orbits eines diskreten, autonomen dynamischen Systems auf Transversalität prüfen können. Unter Verwendung des im ersten Vortrag bewiesenen Satzes reicht es dazu aus, eine exponentielle Dichotomie der Variationsgleichung auf einem hinreichend großen, endlichen Intervall \([-T,T], T \in \mathbb{N}\) nachzuweisen. Im Anschluss daran werden wir die Ergebnisse anhand der Hénon-Abbildung illustrieren.

  • Zdzislaw Brzezniak (York): Stochastic Euler equations in unbounded 2-Ddomains
    18.11.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: I will speak about the existence of a martingale solution to stochastic Euler Equations (with general multiplicative noise) in the Sobolev \(H^{1,q}\cap H^{1,2}\) spaces (based on a 2001 paper with Peszat) and about the existence and uniquence of solutions with bounded vorticity for a specila multiplicative noise (based on a recent unfished work with Flandoli and Maurielli). Somce comments about the existence to stochastic NSEs in unboded domains (based on a work with E. Motyl) wil also be made.

  • Simon Pelster : Spektren kontinuierlicher Dynamischer Systeme
    15.11.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Der Vortrag stellt das Ljapunow-Spektrum und das berechnete Ljapunow-Spektrum für diskrete dynamische Systeme der Form \(u_{t+1}=A_t u_t\) vor. Es wird bewiesen, dass die Ljapunow-Exponenten für Systeme mit \(\sup_{t\in \mathbb{Z}} \|A_t\|=M < \infty\) endlich sind. Außerdem wird ein Kriterium, das die Äquivalenz der beiden Spektren im diskreten Fall liefert, präsentiert.

  • Andrea Lunari (Bielefeld): Optimal Control for a Phase-Field Model of Multiphase Flow
    11.11.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: The optimal control of a multiphase flow is a very interesting and challenging subject from the analytical point of view and leads to concrete industrial applications (e.g. binary alloy, polymer fluids). In this talk I discuss the optimal control of a two-phase fluid flow described by a coupled Cahn-Hilliard-Stokes system, showing the mathematical settings for the problem and its features from an analytical point of view. Then I present a space-time dicretization and an algorithm for the solution of the associated discrete optimal control problem. Finally, I show some first numerical experiments.

  • Adam Andersson (Göteborg): A new approach to weak convergence of SPDEs
    08.11.2013, 14:15, V5-148, Oberseminar Numerik
    Abstract: Weak convergence of numerical approximations for non-linear SPDEs has previously been proved by a use of the Itô formula and the Kolmogorov equation. In this talk I will present a new method to prove weak convergence for semilinear equations with additive noise, not relying neither on the Itô formula nor on the Kolmogorov equation. We linearize the weak error and obtain a remainder term with high order of convergence. For the linearized term we use the fact that the gradient of the test function, evaluated at the solution of the SPDE, is a Malliavin smooth random variable. This allows us to estimate this term by taking the supremum over a bounded subset of random variables from the Malliavin space. After some analysis a use of the Gronwall Lemma is possible. The order of weak convergence, is as expected, twice that of strong convergence. The novelty this result, except for being a new method of proof, is that it allows for test functions with polynomial growth, meaning that we have proved convergence of any moment. This is joint work with Raphael Kruse (ETH) and Stig Larsson (Chalmers).

  • Gerhard Unger (TU Graz): Boundary element methods for eigenvalue problems in acoustics
    28.10.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we present an overview about boundary element methods for eigenvalue problems in acoustics. Our approach is based on a reduction of eigenvalue problems to the boundary of the considered domain. Therefore boundary element methods are in particular suitable for problems which are posed in unbounded domains. Boundary integral formulations of eigenvalue problems lead to nonlinear eigenvalue problems even if the original eigenvalue problem is a linear one. The reason for that is that the eigenvalue parameter occurs nonlinearly in the fundamental solution which is related to the underlying partial differential equation. The used boundary integral formulations for the eigenvalue problems can be considered as eigenvalue problems for holomorphic Fredholm operator-valued functions for which a comprehensive theory is well-established. Within this theory convergence results for the Galerkin discretization of boundary integral formulations of eigenvalue problems are derived. For the numerical solution of the discretized eigenvalue problems the contour integral method is applied. We present several numerical examples of acoustic and vibro-acoustic eigenvalue problems which demonstrate the feasibility of our approach.

  • Koray Arslan : Energieerhaltende Integratoren für Poisson Systeme
    22.07.2013, 16:00, V5-148, Oberseminar Numerik
    Abstract: Mit den sogenannten Poisson Systemen betrachten wir in diesem Vortrag nicht-kanonische Hamiltonsche Systeme und zeigen, dass jede Erhaltungsgröße dieses Systems - insbesondere die Hamiltonsche und die Casimir Funktion - entlang der exakten Lösung erhalten bleibt. Wir stellen anschließend eine neue Klasse von numerischen Verfahren vor, die von E. Hairer & D. Cohen 2011 eigens für Poisson Systeme entwickelt wurde. Wir zeigen, dass diese Verfahren die Hamiltonsche Funktion und quadratische Casimir Funktionen erhalten und dass sie invariant unter linearen Transformationen sind.

  • Marc Winter: Taylor-Approximation invarianter Faserbündel
    19.07.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten eine nicht-autonome Differenzengleichung der Form \(x(n+1)=A(n)x(n)+F(x(n),n)\), \(n \in \mathbb{Z}\). Wir definieren die lokalen und globalen invarianten Faserbündel der Differenzengleichung als Analogon zu den Mannigfaltigkeiten autonomer Differenzengleichungen. Dann untersuchen wir, unter welchen Voraussetzungen diese Faserbündel existieren. Anschließend werden wir diese Faserbündel mit Hilfe der Taylorentwicklung approximieren.

  • Jessica Jandulski : Das Sharkovskii-Theorem für periodische Differenzengleichungen - Teil 2
    15.07.2013, 16:00, V5-148, AG Dynamische Systeme
    Abstract: Während des ersten Vortrags lernten wir das folgende Sharkovskii-Theorem für periodische Differenzengleichungen kennen: Sei \(f_{n\mod p}(x_n)=x_{n+1}\), \(n\in\mathbb{N}\), \(f_n\in C(I,I)\) für alle \(n\in\mathbb{N}\) eine \(p\)-periodische Differenzengleichung, die einen minimalen \(r\)-Zyklus mit \(r\in A_{p,l}\) hat. Dann hat die Differenzengleichung für alle \(A_{p,q}\) mit \(A_{p,l}>A_{p,q}\) in der \(p\)-Sharkovskii-Ordnung einen minimalen \(k\)-Zyklus mit \(k\in A_{p,q}\). Ziel des zweiten Vortrags wird es sein, das nicht-autonome System unter Verwendung des Konzepts der Schiefprodukt-Flüsse in ein autonomes System zu überführen und dann das Theorem mithilfe des klassischen Sharkovskii-Theorems zu beweisen.

  • Martin Rasmussen (Imperial College London) : Bifurcations of random dynamical systems
    08.07.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: Despite its importance for applications, relatively little progress has been made towards the development of a bifurcation theory for random dynamical systems. In this talk, I will demonstrate that adding noise to a deterministic mapping with a pitchfork bifurcation does not destroy the bifurcation, but leads to two different types of bifurcations. The first bifurcation is characterized by a breakdown of uniform attraction, while the second bifurcation can be described topologically. Both bifurcations do not correspond to a change of sign of the Lyapunov exponents, but I will explain that these bifurcations can be characterized by qualitative changes in the dichotomy spectrum and collisions of attractor-repeller pairs. This is joint work with M. Callaway, T.S. Doan, J.S.W Lamb (Imperial College) and C.S. Rodrigues (MPI Leipzig)

  • Raphael Kruse (ETH Zürich): Konsistenz und Stabilität von Galerkin finite Elemente Methoden für Reaktions-Diffusions-Gleichungen
    01.07.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: Wir betrachten Galerkin finite Elemente Methoden für (deterministische) semilineare Reaktions-Diffusions-Gleichungen und betten diese in den abstrakten Rahmen der diskreten Approximationstheorie ein. Basierend auf einer passend für Halbgruppen verallgemeinerten Spijker Norm beweisen wir die Bistabilität des Verfahrens und leiten zweiseitige Fehlerabschätzungen her. Anschließend vervollständigen wir den Konvergenzbeweis mit einer Analyse des Konsistenzfehlers.

  • Paul Voigt (Bielefeld): Das Dirichletproblem für nicht-lokale nicht-symmetrische Operatoren
    28.06.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Im Vortrag wird das elliptische Dirichletproblem für lineare nicht-lokale und nicht notwendigerweise symmetrische Operatoren studiert. Aufgrund der Nicht-lokalität des Operators werden die Randdaten - im Gegensatz zum klassischen Dirichletproblem - auf dem Komplement einer gegebenen Menge vorgegeben. Das Problem wird in einem klassischen Hilbertraum-Setting formuliert. Existenz und Eindeutigkeit von Lösungen wird mit Standardtechniken, wie z.B. der Fredholm-Alternative bewiesen.

  • Alina Girod: Diskretisierung homokliner Orbits im nicht-autonomen Fall
    24.06.2013, 16:00, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten ein kontinuierliches nicht-autonomes Dynamisches System, welches einen transversalen homoklinen Orbit besitzt. Dieses diskretisieren wir zunächst exakt. Diskretisieren wir mit einem Einschritt-Verfahren, welches nah am exakt diskretisierten System ist, so erhalten wir wieder einen transversalen Orbit der nah an dem exakt diskretisierten Orbit liegt. Anschließend werden wir die Theorie an einem Beispiel illustrieren.

  • Robin Flohr : Konvergenz des Strang-Operatorsplittings - Teil 2
    14.06.2013, 14:15, V5-148, AG Dynamische Systeme

  • Robin Flohr : Konvergenz des Strang-Operatorsplittings
    14.06.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: In dem Vortrag wird das Prinzip des Operatorsplittings von Gleichungen der Form \(u_t = Au + uu_x\) vorgestellt. \(A\) ist dabei ein linearer Differentialoperator, so dass die Gleichung wohlgestellt ist. Wichtige Beispiele für \(A\) sind dabei \(Au=u_{xx}\) oder \(A=u_{xxx}\), so dass die Theorie sowohl für die Burgers-Gleichung als auch für die KdV-Gleichung anwendbar ist. Außerdem werden Regularitätsaussagen der getrennten Probleme sowie die Konvergenz erster Ordnung des Strang-Splittings bewiesen.

  • Jessica Jandulski : Das Sharkovskii-Theorem für periodische Differenzengleichungen
    03.06.2013, 16:00, V5-148, AG Dynamische Systeme
    Abstract: Das Sharkovskii-Theorem für autonome Differenzengleichungen behandelt eine stetige, reellwertige Abbildung \(f\), die einen periodischen Orbit der minimalen Periode \(n\) besitzt und liefert die Antwort auf die Frage: Für welche \(m\) existieren dann auch \(m\)-periodische Orbits? Unser Ziel wird es sein, das Sharkovskii-Theorem auf \(p\)-periodische Differenzengleichungen \(x_{n+1}=f_{n\mod p}(x_n)\) zu erweitern. Dafür lernen wir zunächst einen Spezialfall kennen, den wir mithilfe des klassischen Sharkovskii-Theorems beweisen. Anschließend betrachten wir das allgemeinere Sharkovskii-Theorem für \(p\)-periodische Differenzengleichungen und beweisen auch dieses Theorem unter Verwendung des Konzepts der Schiefprodukt-Flüsse mithilfe des klassischen Sharkovskii-Theorems.

  • Sebastian Paul : Dichotomien im Übergang von endlichen zu unendlichen Intervallen
    31.05.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: In diesem Vortrag gehen wir zunächst von einer exponentiellen Dichotomie auf endlichen Intervallen aus. Unter welchen Voraussetzungen lässt sich daraus eine exponentielle Dichotomie auf \(\mathbb{Z}\) zusammensetzen? Wir liefern Bedingungen, unter denen dies möglich ist und beweisen diese Aussage mit Hilfe des Roughness-Theorems.

  • Rudolf Dürksen : Oberhalbstetigkeit von Pullback-Attraktoren
    27.05.2013, 16:00, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten die nichtautonome Differentialgleichung \(\dot{x}=f(x,t),\ x(s)=x_s\), wobei \(f\in C(\mathbb{R}^p\times\mathbb{R},\mathbb{R}^p)\). Im nichtautonomen Fall sind die Lösungen sowohl von der Endzeit \(t\), als auch von der Startzeit \(s\) explizit abhängig, wohingegen im autonomen Fall nur die bereits verstrichene Zeit \(t-s\) relevant ist. In diesem Zusammenhang werden wir den Begriff der Pullback-Konvergenz einführen und einen für nichtautonome Systeme geeigneten Attraktor, den sogenannten Pullback-Attraktor, definieren. Ziel des Vortrags ist es, zu sehen, dass auch der Pullback-Attraktor unter gewissen Voraussetzungen oberhalbstetig ist.

  • Wolf-Jürgen Beyn (Bielefeld): Mathematische Modellbildung, Analyse und Simulation zellulärer Prozesse
    24.05.2013, 16:15, V5-148,
    Abstract: Im Vortrag werden einige Grundprinzipien mathematischer Modellbildung diskutiert, die zum Verständnis des Zusammenwirkens zellulärer Einzelprozesse beitragen können. Zunächst wird auf die verschiedenen Modelltypen eingegangen, die sich durch Begriffspaare wie diskret-kontinuierlich, stationär-zeitabhängig, räumlich homogen-inhomogen, linear-nichtlinear und zufällig-deterministisch unterscheiden lassen. Speziell werden dann einfache Modellgleichungen für enzymatisch ablaufende Stoffwechselprozesse analysiert und Möglichkeiten aufgezeigt, um diese Modelle auf Transportprozesse und genetische regulierte Netzwerke zu erweitern. Dabei entstehen oft große Systeme nichtlinearer Differentialgleichungen, die eine Vielzahl von Parametern enthalten und deren Lösungsverhalten nicht einfach zu überblicken ist. Einerseits werden solche Systeme auf dem Computer simuliert und mit experimentellen Daten verglichen, andererseits versucht man die Modelle so zu reduzieren (Hauptkomponentenanalyse, Pseudostationarität), dass Einsichten in biochemisch relevantes Verhalten gewonnen werden können.

  • Simon Pelster : Spektren kontinuierlicher Dynamischer Systeme
    24.05.2013, 14:00, V5-148, AG Dynamische Systeme
    Abstract: Der Vortrag stellt das Ljapunow-Spektrum und das berechnete Ljapunow-Spektrum kontinuierlicher dynamischer Systeme vor. Unter der Voraussetzung integraler Getrenntheit sind die Spektren für Systeme mit oberer Dreiecksgestalt identisch. Im zweiten Teil wird die Verbindung vom berechneten Ljapunow-Spektrum zum Sacker-Sell-Spektrum für kontinuierliche Systeme hergestellt.

  • Koray Arslan : Symplektizität in numerischen Verfahren und Beispiele symplektischer Integratoren
    17.05.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Nachdem in der ersten Vortragsreihe der Begriff der Symplektizität eingeführt und im Satz von Poincaré gezeigt wurde, dass der exakte Fluss eines Hamiltonschen Systems symplektisch ist, werden wir nun numerische Verfahren konstruieren, von denen wir auch fordern, dass deren diskreter Fluss symplektisch ist.
    Dazu definieren wir erst, was ein symplektisches Verfahren ist, und untersuchen anschließend verschiedene numerische Verfahren auf ihre Symplektizität.
    Dabei richtet sich unser Hauptaugenmerk auf Runge-Kutta-Verfahren, die - wie aus der Numerik II bekannt ist - eine wichtige Klasse von Einschrittverfahren für Anfangswertaufgaben bilden.

  • Koray Arslan: Symplektizität in numerischen Verfahren und Beispiele symplektischer Integratoren
    13.05.2013, 16:00, V5-148, AG Dynamische Systeme
    Abstract: Nachdem in der ersten Vortragsreihe der Begriff der Symplektizität eingeführt und im Satz von Poincaré gezeigt wurde, dass der exakte Fluss eines Hamiltonschen Systems symplektisch ist, werden wir nun numerische Verfahren konstruieren, von denen wir auch fordern, dass deren diskreter Fluss symplektisch ist.
    Dazu definieren wir erst, was ein symplektisches Verfahren ist, und untersuchen anschließend verschiedene numerische Verfahren auf ihre Symplektizität.
    Dabei richtet sich unser Hauptaugenmerk auf Runge-Kutta-Verfahren, die - wie aus der Numerik II bekannt ist - eine wichtige Klasse von Einschrittverfahren für Anfangswertaufgaben bilden.

  • Andre Schenke: Exponentielle Dichotomien für nichtinvertierbare Systeme - Teil 2
    10.05.2013, 14:15, V5-148, AG Dynamische Systeme

  • David Kiesewalter: Die Randelementmethode für das Eigenwertproblem zum Laplaceoprator
    06.05.2013, 16:00, V5-148, AG Dynamische Systeme

  • Abderrahman Boukricha (Tunis): Variational Formulation of Nonlocal and Quasilinear Elliptic Problems and Numerical Analysis of the Weighted p-Laplacian
    26.04.2013, 14:15, V5-148, Oberseminar Numerik
    Abstract: The principle of variational formulation or variational approach for the resolution of well posed problems is to replace the equation by an equivalent formulation which can be solved by Hilbert space methods (in the linear case) or by Minty-Browder methods (in the nonlinear case).
    In this talk, we recall the variational approach of Gregoire Allaire in the classical case for stationary and evolution problems. We prove variational formulations for nonlocal problems (Riesz potentials) and for quasilinear elliptic problems. We then present a numerical analysis for the weighted p-Laplacian.

  • Alexander Mielke (WIAS Berlin): Gradient structures and uniform global decay for reaction-diffusion systems
    25.04.2013, 17:15, V2-210/216,

  • Andre Schenke: Exponentielle Dichotomien für nichtinvertierbare Systeme
    19.04.2013, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Dieser Vortrag behandelt die Verallgemeinerung des Dichotomiebegriffes für nichtinvertierbare dynamische Systeme. Die Definition wird motiviert und es werden elementare Eigenschaften und Beispiele behandelt sowie Unterschiede zum "gewöhnlichen" Dichotomiebegriff für invertierbare Systeme aufgezeigt. Die Projektoren etwa sind im Falle J=Z nicht eindeutig und die Charakterisierung von Bild und Kern der Projektoren mittels Quasibeschränktheit gelingt nur unvollständig. Eine Lösung dieses Problems bietet der Begriff der Regularität, der im zweiten Teil des Vortrags besprochen wird.

  • Abderrahman Boukricha (Tunis) Koautoren: Imed Ghanmi, Rochdi Jebari: Numerical Approximation of solutions of Nonlinear Partial Differential Equations by Homotopy Perturbation Method (HPM) and Adomian Decomposition Method (ADM)
    12.04.2013, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this work, the homotopy perturbation method (HPM) and the Adomian decomposition method (ADM) are presented.
    These methods provide numerical approximations for solutions of non-linear partial differential equations. The solutions of these non-linear problems are approached by series with easily computable partial sums (using Maple for HPM and Mathematica for ADM).
    The numerical approximation in cases, where the exact solutions (resp. other approximations) are known, turns out to be very good (resp. yields better approximations). Ther results show that HPM and ADM are very effective and simple.

  • Dietrich Neumann (Bielefeld) : Diskrete Approximation nichtlinearer Eigenwertprobleme mit Multiplizitäten
    28.01.2013, 16:15, V5-148, AG Dynamische Systeme

  • Wolf-Jürgen Beyn (Bielefeld) : Continuation and Collapse of Homoclinic Tangles
    25.01.2013, 14:15, V5-148, Oberseminar Numerik
    Abstract: By a classical theorem (Birkhoff, Smale, Shilnikov),transversal homoclinic points of maps lead to shift dynamics on a maximal invariant set, also referred to as a homoclinic tangle. In our work we analyze the fate of homoclinic tangles in parameterized systems from the viewpoint of numerical continuation and bifurcation theory. The main bifurcation result shows that the maximal invariant set near a homoclinic tangency, where two homoclinic tangles collide, can be characterized by a set of bifurcation equations that is indexed by a symbolic sequence.
    For the Henon family we investigate in detail the bifurcation structure of multi-humped homoclinic orbits originating from several tangencies. The emerging homoclinic network is explained by combining our bifurcation result with graph-theoretical arguments.
    This is joint work with Thorsten Hüls.

  • Sebastian Schmitz (Lugano): Optimal Realiability in Design for Fatigue Life
    22.01.2013, 16:15, V5-148, Oberseminar Numerik
    Abstract: Fatigue describes the damage or failure of material under cyclic loading. Activation and deactivation operations of technical units are important examples in engineering where fatigue and especially low-cycle fatigue (LCF) play an essential role. A significant scatter in fatigue life for many materials results in the necessity of advanced probabilistic models for fatigue. Moreover, structural shape optimization is of increasing interest in engineering, where with respect to fatigue the cost functionals are motivated by their predictability for the integrity of the component after a certain number of load cycles. But mathematical properties such as the existence of the shape derivatives are desirable, too. Deterministic design philosophies that derive a predicted component life from the average life of the most loaded point on the component plus a safety factor accounting for the scatter band do not have this favorable property, as taking maxima is not a differentiable operation. Here, we present a new local probabilistic model for LCF. This model constitutes a new link between reliability statistics, shape optimization and structural analysis which considers the perspective of fatigue but also fits into the mathematical setting of shape optimization. The cost functionals derived in this way are too singular to be \(H^1\) lower semi-continuous. We therefore have to modify the existence proof of optimal shapes for the case of sufficiently smooth shapes using elliptic regularity, uniform Schauder estimates and compactness of certain subsets in \(C^k(\Omega^\textrm{ext},\mathbb{R})\) via the Arcela-Ascoli theorem, where \(\Omega^\textrm{ext}\) is some shape containing all admissible shapes. Moreover, we extend our existence results to high-cycle fatigue (HCF) and deterministic models of fatigue.

  • Lennart Esdar (Bielefeld): Existenz und Stabilität wandernder Wellen für eine nichtlineare Wellengleichung
    08.01.2013, 16:15, V5-148, Oberseminar Numerik

  • Jochen Röndigs (Bielefeld): Reaction Diffusion Systems on Infinite Lattices
    30.11.2012, 14:15, V5-148, AG Dynamische Systeme
    Abstract: This talk is about the evolution of reaction diffusion systems on an infinite dimensional space and their finite dimensional approximations. The main result is the upper semicontinuity of an approximate attractor on a finite lattice with respect to the attractor of the original system on the infinite lattice. We take a short look at characteristic properties of the equations and then derive a priori estimates which establish the existence of a global attractor, both on the finite and the infinite lattice.

  • Rudolf Dürksen: Unterhalbstetigkeit von Attraktoren
    20.11.2012, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Wir betrachten eine autonome Differentialgleichung der Form \(\frac{du}{dt}=f(u)\), \(u(0)=U\in\mathbb R^p\), die mit einem Einschrittverfahren \(U_{n+1}=S_{\Delta t}^1U_n\), \(U_0=U\) gelöst wird. Für den diskretisierten Attraktor \(\mathcal{A}_{\Delta t}\) haben wir gesehen, dass die Oberhalbstetigkeit \(\text{dist}\left(\mathcal{A}_{\Delta t},\mathcal{A}\right)\rightarrow 0\) gegeben ist. Wir werden zeigen, dass unter zusätzlichen Voraussetzungen auch die Unterhalbstetigkeit \(\text{dist}\left(\mathcal{A},\mathcal{A}_{\Delta t}\right)\rightarrow 0\) gegeben ist, sodass insgesamt \(\text{dist}_H\left(\mathcal{A},\mathcal{A}_{\Delta t}\right)\rightarrow 0\) für \(\Delta t \to 0\) gilt.

  • Andre Schenke: Hyperzyklische Operatoren und der Satz von Grivaux
    16.11.2012, 14:15, V5-148, AG Dynamische Systeme
    Abstract: Der Satz von Grivaux gibt eine Charakterisierung derjenigen Mengen eines separablen unendlich-dimensionalen Banachraumes an, die Orbits eines hyperzyklischen Operators sind. Behandelt werden die grundlegenden Ideen für die Formulierung des Satzes von Grivaux, der Beweis im Banachraumfall sowie eine kurze Beweisskizze für den Fall von Fréchet-Räumen mit einer stetigen Norm.

  • Alina Girod: Diskretisierung heterokliner Orbits
    16.10.2012, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Erste Betrachtung ist ein kontinuierliches Dynamisches System, wobei der Begriff nicht-entarteter Verbindungsorbit eingeführt wird. Diese und 1-tangentiale Orbits betrachten wir dann im diskretisierten Fall. Zwischenziel ist es zu zeigen, dass diskretisierte Verbindungsorbits des kontinuierlichen Systems 1-tangentiale nicht-entartete heterokline Orbits des \( \varepsilon \)-Flusses sind. Allgemeines Ziel ist es zu zeigen, dass eine Diskretisierung mit einem Einschritt-Verfahren unter gewissen Annahmen mindestens zwei 1-tangentiale nicht-entartete heterokline Orbits besitzt.

  • Thorsten Hüls: Homoclinic trajectories of non-autonomous maps
    09.10.2012, 16:15, V5-148, Oberseminar Numerik
    Abstract: For time-dependent dynamical systems of the form \(x_{n+1} = f_n(x_n), n \in \mathbb{Z}\) homoclinic trajectories are the non-autonomous analog of homoclinic orbits from the autonomous world. More precisely, two trajectories \((x_n)_{n\in\mathbb{Z}}\), \((y_n)_{n\in\mathbb{Z}}\) are called homoclinic to each other, if \(\lim_{n\to \pm \infty} \|x_n - y_n\| = 0\). Two boundary value problems are introduced, the solution of which yield finite approximations of these trajectories. Under certain hyperbolicity assumptions, we prove existence, uniqueness and error estimates. Extending these ideas, we also propose adequate notions for heteroclinic orbits in non-autonomous systems. The resulting algorithms and error estimates are illustrated by an example.

  • Stefanie Hittmeyer (Auckland): Interacting global manifolds in a planar map model of wild chaos
    20.07.2012, 14:15, V5-148, Oberseminar Numerik
    Abstract: We study a non-invertible planar map that has been suggested by Bamon, Kiwi and Rivera-Letelier as a model for a new type of chaotic dynamics in continuous-time dynamical systems of dimension at least five; one also speaks of wild Lorenz-like chaos. This map opens up the origin (the critical point) to an open disk and wraps the plane twice around it; inside this disk there are no preimages. The bounding critical circle and its images, together with the critical point and its preimages form the so-called critical set. This set interacts with a saddle fixed point and its stable and unstable sets.
    Advanced numerical techniques enable us to study how the stable and unstable sets change as a parameter is varied along a path towards the wild chaotic regime. We find sequences of bifurcations, which are of two types. First, there are bifurcations that also occur in invertible maps, such as homoclinic tangencies. Second, we find bifurcations specific to non-invertible maps: interactions of the stable and unstable sets with the critical set, which also cause changes (such as self-intersections) of the topology of these global invariant sets. Overall, a consistent sequence of both types of bifurcations emerges, which we present as a first attempt towards explaining the geometric nature of wild chaos.

  • Martin Arnold: Ein Lie-Gruppen-DAE-Integrator
    09.07.2012, 16:15, V5-148, Oberseminar Numerik
    Abstract: Lage und Orientierung des Starrkörpers lassen sich ohne Singularitäten als Elemente geeigneter Lie-Gruppen beschreiben. Schon 1989 haben Géradin und Cardona diese Darstellung zu einer Finite- Elemente-Beschreibung flexibler Mehrkörpersysteme verallgemeinert. Bezieht man die für mechanische Mehrkörpersysteme typischen (holonomen) Zwangsbedingungen ein, so ergeben sich differentiell-algebraische Systeme (engl.: differential-algebraic equations, DAEs) vom Index 3 auf einer (Matrix-)Lie-Gruppe. Bei der direkten Zeitintegration dieses Index-3-Systems mit dem aus der Strukturdynamik bekannten Generalized-/(alpha/)-Verfahren) beobachtet man - ebenso wie bei Anwendung dieses Verfahrens in linearen Räumen - eine Ordnungsreduktion zu Beginn der Integration. Eine detaillierte, auf die zugrunde liegende Lie-Gruppen-Struktur zugeschnittene Konvergenzanalyse zeigt, wie die Ordnungsreduktion durch modifizierte Startwertedes Zeitintegrationsverfahrens vermieden werden kann. Die Ergebnisse der theoretischen Untersuchungen werden durch numerische Tests für einfache Benchmarkprobleme verifiziert.

  • Andrea Walther (Paderborn): On an Inexact Trust-region Approach for Inequality Constrained Optimization
    29.06.2012, 12:45, V5-148, Oberseminar Numerik
    Abstract: This talk presents a trust-region SQP algorithm for the solution of minimization problems with nonlinear inequality constraints. The approach works only with an approximation of the constraint Jacobian. Hence, it is well suited for optimization problems of moderate size but with dense constraint Jacobian. The accuracy requirements for the presented first-order global convergence result can be verified easily during the optimization process. Numerical results for some test problems are shown.

  • Sonja Cox (Universität Innsbruck) : Pathwise estimates for the implicit Euler scheme for SDEs in Banach spaces
    08.06.2012, 14:15, V5-148, Oberseminar Numerik
    Abstract: In the first part of my talk I will explain what is meant by pathwise estimates for an approximation scheme of a stochastic differential equation (SDE), and why such estimates are of importance. In recent work by Jan van Neerven and myself, we obtained pathwise estimates for the implicit Euler scheme for SDEs in Banach spaces. In the second half of the talk I will sketch how we obtained these results and indicate what challenges arise when working in Banach spaces.

  • Wilhelm Stannat (TU Berlin, Bernstein Netzwerk) : Stochastic stability of travelling waves in the Nagumo equation
    01.06.2012, 14:15, V5-148, Oberseminar Numerik
    Abstract:

  • Michael Scheutzow (TU Berlin) (Projekte A3, B3, B4) : Uniqueness of invariant measures via asymptotic coupling with applications to stochastic delay equations
    25.05.2012, 14:00!!, V5-148,
    Abstract: We provide sufficient conditions for the uniqueness of an invariant measure for a Markov process in terms of the existence of a generalized asymptotic coupling. This method is particularly useful in cases in which the transition probabilities for different initial conditions are mutually singular (and hence classical methods for proving uniqueness fail). We apply the result to stochastic delay equations.
    This is joint work with Martin Hairer and Jonathan Mattingly.

  • Heiko Prange : Hinreichende Bedingungen für LR-Chaos in zeitdiskreten dynamischen Systemen
    21.05.2012, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Ähnlich wie die chaotische Dynamik des Shift-Operators auf der Menge der Symbole 0 und 1 lässt sich der Begriff des Links-Rechts Chaos auf Teilmengen L und R eines zeitdiskreten dynamischen Systems definieren. Die Kern-Idee zum Aufspüren von LR-Chaos in zeitdiskreten dynamischen Systemen ist es, periodische Punkte zu vorgegebenen Links-Rechts Sequenzen zu finden. Diese periodischen Punkte kann man als Fixpunkte von iterierten Funktionen betrachten. So führt der Miranda-Fixpunktsatz zu Gebieten mit LR-chaotischer Dynamik.

  • Christian Pötzsche (Klagenfurt) : Feinstruktur des Dichotomie-Spektrum
    18.05.2012, 14:15, V5-148, Oberseminar Numerik
    Abstract: Das Dichotomie-Spektrum (auch dynamisches oder Sacker-Sell Spektrum) ist ein wesentlicher Begriff innerhalb der Theorie nichtautonomer dynamischer Systeme, da es zentrale Information zur Stabilität, Hyperbolizität und Robustheit von Lösungen enthält. Aktuelle Anwendungen in der Verzweigungstheorie erfordern jedoch eine detailliertere Einsicht in dessen Feinstruktur. Auf dieser Basis untersuchen wir eine hilfreiche Verbindung zwischen Dichotomie-Spektrum und Operator-Theorie, welche das Langzeitverhalten nichtautonomer Gleichungen mit dem Punkt-, Surjektivitäts- oder Fredholm-Spektrum gewichteter Shift-Operatoren in Beziehung setzt. Dieser Zusammenhang führt auf entsprechende Teilmengen des Dichotomie-Spektrums, welche nicht nur Verzweigungen bereits auf linearer Ebene klassifizieren, sondern auch Beweise über das asymptotische Verhalten von Differential- und Differenzengleichungen vereinfacht.

  • Rudolf Dürksen (Bielefeld) : Oberhalbstetigkeit von Attraktoren
    07.05.2012, 16:15, V5-148, AG Dynamische Systeme
    Abstract: Sei eine autonome Differentialgleichung der Form \(\frac{du}{dt}=f(u), u(0)=U\in\mathbb R^p\), gegeben. Bekanntlich kann diese Differentialgleichung mit einem Einschrittverfahren \(U_{n+1}=S_{\Delta t}^1U_n, U_0=U\) gelöst werden. Wir werden das Verhalten des diskretisierten Attraktors \(\mathcal{A}_{\Delta t}\) untersuchen und dabei feststellen, dass in unserem Fall die Oberhalbstetigkeit gegeben ist, d. h. dass \(dist\left(\mathcal{A}_{\Delta t},\mathcal{A}\right)\rightarrow 0\) gilt.

  • Jan Giesselmann (Stuttgart) : Some ideas for the numerical discrtization of the Navier-Stokes-Korteweg model
    30.04.2012, 16:15, V5-148, Oberseminar Numerik
    Abstract:

  • Sergey Tikhomirov : Shadowing lemma for partially hyperbolic systems
    30.01.2012, 16:15, V5-148, Oberseminar Numerik
    Abstract: We say that diffeomorphism \(f\) of a manifold \(M\) is partially hyperbolic if tangent bundle of \(M\) admits an invariant splitting \(E^s + E^c + E^u\), such that \(E^s\) and \(E^u\) are uniformly hyperbolic and \(E^c\) is not. If \(E^c \) is empty diffeomorphism is uniformly hyperbolic. Shadowing lemma says that in hyperbolic systems any pseudotrajectory can be shadowed by an exact trajectory. We introduce notion of central pseudotrajectory and prove that in partially hyperbolic systems any pseudotrajectory can be shadowed by a central pseudotrajectory.

  • Annika Lang (ETH Zürich): Simulation of stochastic processes
    23.01.2012, 16:15, V5-148, Oberseminar Numerik
    Abstract: Hilbert-space-valued stochastic processes such as Q-Wiener processes are in general the driving noise of stochastic partial differential equations (SPDEs for short). To approximate the solution of an SPDE, it is in general necessary to approximate the driving noise. In this talk, different approximation methods for stochastic processes and the corresponding Ito integrals are introduced and their simulations are presented. As an application to the approximation of solutions of SPDEs it is shown how to equilibrate the discretization errors of the space and time approximation of the SPDE and the error of the driving noise approximation.

  • Lennart Esdar : Solitärwellen in Hamiltonschen Systemen
    20.01.2012, 14:15, V5-148, AG Dynamische Systeme
    Abstract:

  • Christian Lubich (Tübingen): Modulated Fourier expansions for highly oscillatory problems
    09.12.2011, 14:15, V5-148, Oberseminar Numerik
    Abstract: Modulated Fourier expansions are an analytic technique for understanding the behaviour of weakly nonlinear oscillatory problems over very long times. The technique applies to highly oscillatory ODEs, to particle systems such as the Fermi-Pasta-Ulam lattice, to Hamiltonian PDEs such as nonlinear Schrödinger and wave equations, as well as to their numerical discretizations. The approach first came up about a decade ago in the numerical analysis of highly oscillatory ODEs, where it explained remarkable long-time energy conservation properties of numerical integrators, and has since been used to analyse long-time properties of various types of problems as mentioned above, both for the continuous equations and their numerical discretizations. In addition to their role as an analytical tool originating from numerics, modulated Fourier expansions have also been found useful as a numerical approximation method for highly oscillatory problems. Most of the talk is based on joint work with Ernst Hairer, some parts also with David Cohen, Ludwig Gauckler and Daniel Weiss.

  • Matthias Ehrhardt : Absorbing Boundary Conditions for Hyperbolic Systems
    05.12.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: This talk deals with absorbing boundary conditions (ABCs) for hyperbolic systems in one and two space dimensions. We prove the strict well-posedness of the resulting initial boundary value problem in 1D. Afterwards we establish the GKS-stability of the corresponding Lax-Wendroff-type finite difference scheme. Hereby, we have to extend the classical proofs, since the (discretized) ABCs do not t the standard form of boundary conditions for hyperbolic systems.
    In the second part we present the approach of deriving so-called discrete absorbing boundary conditions, i.e. ABCs constructed on a purely discrete level. These discrete ABCs are better adapted to the interior scheme: they lead to less unphysical reflections and the resulting overall scheme has better stability properties. Finally, we sketch briefly how ABCs can be derived for nonlinear hyperbolic systems.

  • Thorsten Rieß (Universität Konstanz): N-heteroclinic orbits near non-reversible homoclinic snaking
    28.11.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: Non-reversible homoclinic snaking of a codimension-1 homoclinic orbit to an equilibrium is a phenomenon that is known to occur near certain heteroclinic equilibrium-to-periodic (EtoP) cycles. We show numerically that there exist other connecting orbits in the neighbourhood of the homoclinic snaking for a specific family of three-dimensional vector fields. In particular, we use a numerical method based on Lin's method to compute codimension-1 PtoE connecting orbits that take additional excursions along the EtoP cycle before connecting up, so-called N-heteroclinic PtoE orbits. It turns out that the N-heteroclinic PtoE orbits exist on isolas in parameter space.

  • Sergei Pilyugin (St. Petersburg): Lipschitz shadowing and structural stability: the case of flows
    11.10.2011, 16:30, V5-148, Oberseminar Numerik
    Abstract: Recently, it was shown that for diffeomorphisms, Lipschitz shadowing is equivalent to structural stability (S.Yu. Pilyugin and S.B. Tikhomirov, Nonlinearity, vol. 23, 2509-2515, 2010). In this talk, we discuss a similar result for flows and explain the appearing difficulties (the main difficulty is created by the absence of Mane's theorem characterizing structural stability in terms of strong transversality). This is a joint research with K.Palmer and S.Tikhomirov.

  • Richard Norton (Oxford): Finite Element Approximation of an H1 Gradient Flow
    11.07.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: I consider the discretization error in space and time of an H1 gradient flow for an energy integral where the energy density is given by the sum of a double-well potential term and a bending energy term. This problem is equivalent to a nonlinear heat equation with nonlocal nonlinearity. The approach for the error analysis is to adapt standard error analysis theory developed for nonlinear heat equations to bound the discretization error in terms of the mesh size and time step as well as energy parameters. In particular, I carefully track how the size of the bending energy affects the error bounds.

  • Piotr Gwiazda: On scalar hyperbolic conservation laws with a discontinuous flux
    04.07.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: We study the Cauchy problem for scalar hyperbolic conservation laws with fluxes that can have jump discontinuities with respect to the unknown and only measurable with respect to the space variable. We introduce a new concept of entropy weak and measure-valued solution that is consistent with the standard one for continuous fluxes. We then answer the question as to what kind of properties the fluxes should posses in order to establish the existence and/or uniqueness of various notions of solutions. In any space dimension we establish the existence of measure-valued entropy solution for fluxes having jump discontinuities, under additional assumptions we prove existence of weak solutions.

  • Ewelina Zatorska: On a new approach applied to the time--discretization of the compressible Navier--Stokes equations
    20.06.2011, 16:15, V5-148, Oberseminar Numerik

  • Matthias Groncki: Markovketten und der Metropolis-Algorithmus
    10.06.2011, 14:15, V5-148, AG Dynamische Systeme

  • Gert Lube (Göttingen): A Projection-based Variational Multiscale Method for Turbulent Incompressible Flows
    06.06.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: We consider the Navier-Stokes Fourier model for time-dependent, non-isothermal, incompressible flows. This nonlinear evolution problem has a generalized solution. Moreover, in case of a regularization with the well-known Smagorinsky turbulence model, it is uniquely solvable. Unfortunately, the latter model is too diffusive in application to turbulent flows. As a remedy, a variational multiscale (VMS) method for the large-eddy simulation is considered.
    Following a general proposal in [1], our VMS-approach relies on local projection of the velocity deformation tensor and the temperature gradient together with a grad-div stabilization of the divergence-free constraint. Semi-discrete stability and a priori error estimates are derived in the case of inf-sup stable approximation of velocity and pressure, see [2, 3]. In particular, rather general nonlinear and piecewise constant coefficients of the subgrid models for the unresolved scales of velocity and pressure are allowed, including the classical Smagorinsky model. We give a critical discussion of the results in view of the employed Gronwall argument. Moreover, we discuss aspects of the time discretization and of its analysis.
    Finally, we present and discuss numerical simulations for basic benchmark problems like decaying homogeneous isotropic turbulence, channel flow and natural convection in a differentially heatedcavity.

    References
    [1] W. Layton, A connection between subgrid scale eddy viscosity and mixed methods. Appl. Math. Comput. 133 (2002), 147-157.
    [2] L. Röhe, and G. Lube, Analysis of a variational multiscale method for Large-Eddy simulation and its application to homogeneous isotropic turbulence, Comput. Meths. Appl. Mech. Engrg. 199 (2010), 2331-2342.
    [3] J. Löwe, and G. Lube, A projection-based variational multiscale method for Large Eddy simulation with application to non-isothermal free convection problems, NAM Preprint, Georg-August-Universität zu Göttingen, 2010. Accepted for Math. Model. Meths. Appl. Sc. (5/2011).

  • Denny Otten (Bielefeld): Exponential decay of two-dimensional rotating waves
    03.06.2011, 14:15, V5-148, AG Dynamische Systeme

  • Marcin Malogrosz: A Model of Morphogen Transport Well-Posedness and Asymptotical Behaviour
    30.05.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: Morphogen transport (MT) is a process occurring in the tissue of life organisms, affecting cell differentiation. There is a vast literature concerning modeling of MT but as for now there is still no consensus on what is the exact mechanism of the movement of morphogen particles. Various types of diffusion, bucket brigade, reactions with other particles are among those being considered.
    I will present my recent results concerning well-posedness and asymp- totical behavior of the solutions of the model proposed in [1] (semilinear parabolic PDE coupled with ODE), where MT is being modeled by passive diffusion and binding-unbinding reactions with receptors.
    My results are nontrivial extension of those obtained in [2], where the same model is being considered in 1D setting. Using theory of analytic semigroups I improve dimension of the domain (from 1 to arbitrary) and topology of the convergence of solution to unique equilibrium (from \(L_2 \times L_2\) to \(C^{1,\alpha} \times C^{0,\alpha}\)).

    References
    [1] Lander, A. D., Nie, Q., Wan, Y. M. Do Morphogen Gradients Arise by Diffusion? Dev. Cell, Vol. 2, pp. 785-796.
    [2] Krzyzanowski, P., Laurençcot, P., Wrzosek, D. Well-posedness and con- vergence to the steady state for a model of morphogen transport, SIAM J.MATH. ANAL. Vol. 40, No. 5, pp. 1725-1749.

  • Raphael Kruse (Bielefeld): FEniCS: Finite Elements in Computer Science eine Software zur Loesung elliptischer und parabolischer Aufgaben
    13.05.2011, 14:15, V5-148, AG Dynamische Systeme

  • Maria Lopez Fernandez (Uni Zürich): Contour integral methods for parabolic equations
    09.05.2011, 16:15, V5-148, Oberseminar Numerik

  • Andrzej Warzynski: 30 Years of Residual Distribution Schemes for Hyperbolic Conservation Laws
    02.05.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: The most popular schemes for hyperbolic conservation laws are based on 1-dimensional concepts (i. e. Riemann solver) which are then heuristically extended and applied to flow problems in more than 1 space dimension. Recently, intensive research has been being carried out focused on the development of `multidimensional upwind' schemes. This new class of numerical algorithms is far better able to incorporate genuinely multidimensional phenomena described by conservation laws and thus to predict the fluid flow more accurately. In this talk I shall first briefly justify the need for genuinely multidimensional approach and then describe a particular class of multidimensional upwind schemes, namely those developed within the Residual Distribution (RD) framework. This will include design principles for the steady state RD schetime-dependent problems. Finally, I shall focus on the recently proposed explicit Runge-Kutta RD [1] and discontinuous RD schemes [2], and discuss the possibility of combining these two approaches. This is an ongoing research conducted in collaboration with M. E. Hubbard and M. Ricchiutto. [1] R. Abgrall, M. Ricchiuto 'Explicit Runge-Kutta residual distribution schemes for time dependent problems: second order case.' J. Comput. Phys. 229(16), 5653--5691, 2010. [2] M. E. Hubbard 'Discontinuous fluctuation distribution.' J. Comput. Phys. 227(24), 10125--10147, 2008.

  • Janning Barembruch (Bielefeld): Diskretisierung der Hopf-Bifurkation
    15.04.2011, 14:15, V5-148, AG Dynamische Systeme

  • Guy Vallet (Pau): On some Barenblatt's problems
    11.04.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we will be interested in the problem of Barenblatt's type: \(f(\partial_{t}u)-\Delta_pu - \epsilon \Delta \partial_{t}u =g\quad \textrm { in }\ Q.\) In a first part, we will consider the hilbertian case \(p=2\), then when \(p> \frac{2d}{d+2}\) and when \(p\) is a function of \(x\). We finish with some numerical simulations of the hilbertian case.

  • Janning Barembruch (Bielefeld): Diskretisierung der Hopf-Bifurkation
    08.04.2011, 14:15, V5-148, AG Dynamische Systeme

  • Raphael Kruse : Finite-Elemente Methoden für PDEs
    04.02.2011, 14:15, V5-148, AG Dynamische Systeme

  • Heiko Berninger (FU Berlin): On Domain Decomposition Methods for Nonlinear Transmission Problems
    31.01.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: Consider a nonoverlapping decomposition of a domain \(\Omega\) into subdomains \(\Omega_1\) and \(\Omega_2\). It is well known that instead of solving \(-\triangle u = f\) on \(\Omega\), one can solve this equation on \(\Omega_1\) and on \(\Omega_2\) if one additionally obeys the transmission conditions \(u_1|_\Gamma = u_2|_\Gamma\) and \(\frac{\partial u_1}{\partial n} = \frac{\partial u_2}{\partial n}\) across the interface \(\Gamma = \Omega_1 \cap \Omega_2\). Furthermore, domain decomposition methods like the Dirichlet-Neumann or the Robin method can be used to solve the transmission problem. But what if the continuity condition \(u1|_\Gamma = u2|_\Gamma\) is replaced by the more general one \(F_1(u_1|_\Gamma) = F_2(u_2|_\Gamma)\) with - possibly nonlinear - operators \(F_1, F_2\) acting on the trace space \(H^{\frac{1}{2}}_{00} (\Gamma)\)? We discuss variations of this situation, sketch proofs for well-posedness and convergence of corresponding nonlinear domain decomposition methods, and address open questions as well as limitations inherent in the proofs. These situations occur in nature when we intend to simulate saturated - unsaturated groundwater flow in a way that we find quite nice. This is because we have a solver-friendly discretization for the Richards equation in homogeneous soil and monotone multigrid as a powerful solver in this case. We present numerical examples which also address optimization of the domain decomposition methods. Joint work with: R. Kornhuber, O. Sander (FU Berlin), M. Discacciati (EPFL Lausanne)

  • Raphael Kruse : Finite-Elemente Methoden für PDEs
    28.01.2011, 14:15, V5-148, AG Dynamische Systeme

  • José Augusto Ferreira (Coimbra):
    24.01.2011, 17:15, V5-148, Oberseminar Numerik
    Abstract: Integro-differential equations of Volterra type arise, naturally, in many applications such as for instance heat conduction in materials with memory, diffusion in polymers and diffusion in porous media. The aim of this talk is to presente supraconvergent finite difference methods for such integro-differential equations. As these finite difference methods can be seen as piecewise linear finite elements method combined with special quadrature formulas, our results are superconvergence results in the finite element language.

  • Bernd Simeon (Kaiserslautern): Transiente Sattelpunktprobleme und Anwendungen in der Mechanik
    24.01.2011, 16:15, V5-148, Oberseminar Numerik
    Abstract: n. a.

  • Jens Rottmann-Matthes : Optimale Integralabschätzungen für die Laplacetransformation
    21.01.2011, 14:15, V5-148, AG Dynamische Systeme

  • Yi Zhou : Die Takens-Bogdanov Singularitaet
    14.01.2011, 14:15, V5-148, AG Dynamische Systeme

  • Sven Kreimer-Huenke : Spektralmethoden fuer Evolutionsgleichungen
    17.12.2010, 14:15, V5-148, AG Dynamische Systeme

  • Filip Rindler (Oxford): Rigidity for some differential inclusions involving the gradient and the symmetrized gradient
    14.12.2010, 18:00, V5-148, Seminar Evolutionsgleichungen
    Abstract: We look at (smooth) functions \(u:\mathbb{R}^2\to\mathbb{R}^2\) whose gradient can be written in the form \(\nabla u(x)=P g(x)\) for a fixed \(\mathbb{R}^{2\times 2}\)-matrix \(P\) and a smooth scalar function \(g:\mathbb{R}^2\to \mathbb{R}\). Similarly, replacing the gradient by the symmetrized gradient, we consider (smooth) solutions \(u:\mathbb{R}^2\to\mathbb{R}^2\) of \(\left( \nabla u(x)+ (\nabla u(x))^T\right)/2 = Pg(x),\) with \(P\) a fixed symmetric \(\mathbb{R}^{2\times 2}\)-matrix and \(g\) as before. I will establish conditions on the existence of such solutions, depending on the value of \(P\), and I will prove some (probably unexpected) 'rigidity' properties of any function \(u\) satisfying one of the above properties. The situation in two dimensions already contains all the essential features and exposes fascinating connections to Harmonic Function Theory and Complex Analysis. Whereas the presented results are new (particularly in the case of the symme trized gradient) and are a core ingredient in the results described in my se minar talk, the discussion is completely elementary and involves only first-year multi-dimensional Differential Calculus. I will also point out a few references for further study of such 'rigidity arguments'.

  • Filip Rindler (Oxford): Minimization problems in the space BD of functions of bounded deformation
    13.12.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: The space BD of functions of bounded deformation consists of all L^1-functions whose distributional symmetrized derivative (defined by duality with the symmetrized gradient (Δ u + Δ u^T)/2) is representable as a finite Radon measure. Such functions play an essential role in modern theories of (linear) elasto-plasticity in a variational framework. In this talk, I will present the first general theorem on solvability of minimization problems for integral functionals with linear growth on the whole space BD. The main novelty is that we allow for non-vanishing Cantor-parts in the symmetrized derivative, corresponding to fractal phenomena in nature. The proof is accomplished via Jensen-type inequalities for generalized Young measures and a construction of good blow-ups, which is based on local rigidity arguments for some differential inclusions involving symmetrized gradients. This strategy allows us to prove the crucial lower semicontinuity result without an Alberti-type theorem in BD, which is not available at present. A similar strategy also allows to considerably simplify the proof of the classical lower semicontinuity theorem in the space BV of functions of bounded variation.

  • Eduard Feireisl (Prag): Asymptotic behavior of compressible viscous fluids
    09.12.2010, 17:15, V3-201, Mathematisches Kolloquium
    Abstract: We discuss the long-time behavior of solutions to energetically closed fluid systems. By this we mean that the system possesses an energy functional, the value of which is conserved in time, and an entropy, the total amount of which is nondecreasing. Various topics are addressed: Equilibrium solutions, thermodynamic stability, the existence of attractors, boundedness of globaltrajectories

  • Eduard Feireisl (Prag): Singular limits of compressible fluids driven by large external forces
    07.12.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: We consider a compressible fluid excited by large external forces. Using the abstract result of Kato we show that the acoustic component of the velocity vanishes in the incompressible regime although there is a strong interaction between the force and acoustic waves. Applications are given to rotating fluid systems.

  • Lina Fruendt : Symbolische Dynamik und transversale homokline Punkte
    03.12.2010, 14:15, V5-148, AG Dynamische Systeme

  • Martin Stynes (Cork): A new finite element method for singularly perturbed reaction-diffusion problems
    30.11.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: Consider the singularly perturbed linear reaction-diffusion problem -ε^2 Δ u + bu = f in Ω ⊂ R^d, u=0 on δΩ, where 0 < ε << 1, b > 0 and d≥ 2. It is argued that for this type of problem, the standard energy norm is too weak a norm to meas ure adequately the errors in solutions computed by finite element methods. A stronger norm is introduced and a mixed finite element constructed whose solution is quasi-optimal in this new norm, and a duality argument is used to show that this solution attains a higher order of convergence in the L^2 norm. Error bounds derived from these analyses are presented for the cases d=2,3. For a problem posed on the unit square in R^2, an error bound that is uniform in ε is derived when the new method is implemented on a Shishkin mesh. Numerical results are presented to show the superiority of the new method over current finite element methods for singularly perturbed reaction-diffusion problems.

  • Lina Fruendt : Symbolische Dynamik und transversale homokline Punkte
    26.11.2010, 14:15, V5-148, AG Dynamische Systeme

  • Aneta Wróblewska: Generalized Stokes system in Orlicz spaces
    22.11.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: The talk concerns the generalized Stokes system ∂_t u - div S(t, x,Du) + ∇ p = f in (0, T) × Ω div u = 0 in (0, T) × Ω u(0, x) = u_0 in Ω u(t, x) = 0 on (0, T) × ∂ Ω, with the nonlinear viscous term having growth conditions prescribed by an N-function. We will consider the case of monotone functions. Our main interest is directed to relaxing the assumptions on the N-function. To prove existence of weak solutions to our equations we will show the Korn-Sobolev inequality for anisotropic Orlicz spaces and the fact that closures of smooth compactly supported functions w.r.t. modular and weak star topology of symmetric gradient coincides.

  • Jens Rottmann-Matthes : Laplace-Transformation und Stabilitaet der konvektiven Waermeleitungsgleichung
    19.11.2010, 14:15, V5-148, AG Dynamische Systeme

  • François Murat (Paris) : How to solve second order elliptic equations with right-hand side in L^1
    18.11.2010, 17:15, V3-201, Mathematisches Kolloquium
    Abstract: In this lecture, I will consider the problem: find u such that -div(A(x)Du) = f in Ω, u = 0 on Ω when the matrix A is coercive with measurable bounded coefficients and when f belongs to L^1(Ω). The main difficulty of the problem is to define a convenient notion of solution. Such a definition (the 'solution by transposition') was introduced by G. Stampacchia in 1973. However, this definition is essentially restricted to the linear case. In this lecture, I will present the notion of 'renormalized solution', which can be extended in a natural way to the case of a second order monotone operator in divergence form posed on W^{1,p}_0 (Ω) Definition: u is a renormalized solution of the problem if u : Ω → ℝ is measurable and a.e. finite T_n(u) ∈ H^1_0 (Ω) for every n > 0, 1/n ∫ |DT_n(u)|^2 → 0 as n → + ∞, -div(h(u)A(x)Du)+h'(u)A(x)DuDu = h(u)f in D'(Ω) for every h ∈ C^1_c (ℝ) This definition allows one to prove that the problem has a renormalized solution, that this renormalized solution is unique, and that it depends continuously on f, i.e. that in this framework the problem is well posed in the sense of Hadamard.

  • Thomas Hanning : Numerische Berechnung invarianter Mannigfaltigkeiten
    05.11.2010, 16:00, V5-148, AG Dynamische Systeme

  • Wolf-Juergen Beyn (Bielefeld) : Eine Integralmethode fuer nichtlineare Eigenwertprobleme
    29.10.2010, 14:15, V5-148, AG Dynamische Systeme

  • Petra Wittbold (Essen): On a nonlinear elliptic-parabolic integro-differential equation with L^1-data
    27.10.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: We consider an initial-boundary-value problem for a nonlinear elliptic-parabolic integro-differential equation. Equations of this type have been proposed to model flow through porous media with memory effects and nonlinear heat flow in certain dielectric materials at low temperatures. Following classical results by Gripenberg, existence and uniqueness of a generalized solution to an associated abstract operator integro-differential equation can be shown for abitrary L^1-data. We study the question of regularity of this generalized solution and discuss conditions that ensure that the generalized solution is a strong, weak, entropy or renormalized solution.

  • Thorsten Rohwedder (Berlin): The electronic Schrödinger equation and an analysis for the continuous Coupled Cluster method
    25.10.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: Many properties of atoms, molecules and solid states are described quite accurately by solutions Ψ of the electronic Schrödinger equation H Ψ = E Ψ , an extremely high-dimensional operator eigenvalue equation for the Hamiltonian H of the system under consideration. Of utmost interest is the smallest eigenvalue of H and the corresponding eigenfunction, giving the ground state energy and the electronic wave function describing the ground state, respectively.
    In the first part of this talk, the audience is introduced to the electronic Schrödinger equation and the typical problems that arise when dealing with this equation. We will then introduce the Coupled Cluster method, a method that is standardly used in quantum chemistry for highly accurate calculations. Coupled Cluster (CC) is standardly formulated as an ansatz for the approximation of the Galerkin solution of the Schrödinger equation with in a given discretisation [1].
    We globalise this ansatz to infinite dimensional spaces, thus obtaining an equivalent reformulation of the original, continuous Schrödinger equation in terms of a root equation for a nonlinear operator A, corresponding to the finite dimensional CC function f. We show local strong monontonicity of the CC function, derive some existence and uniqueness results and prove a goal-oriented error estimator [2] for the ground state energy. We conclude with a short discussion of the algorithmic treatment of the CC root equation.
    [1] R. Schneider, Num. Math. 113, 3, 2009.
    [2] R. Becker, R. Rannacher, Acta Numerica 2000 (A. Iserlet, ed.), Cambridge University Press, 2001

  • Etienne Emmrich (Bielefeld): Doubly nonlinear evolution equations of second order: Existence and fully discrete approximation
    19.10.2010, 18:00, V5-148, Seminar Evolutionsgleichungen
    Abstract: The initial-value problem for doubly nonlinear evolution equations of the type u'' + Au' + Bu = f is studied. The time-dependent operator A is assumed to satisfy a certain growth condition and is supposed to be the sum of a monotone, coercive and hemicontinuous principal part and a strongly continuous perturbation. The operator B is supposed to be the sum of an operator that induces an inner product and a non-monotone perturbation fulfilling a certain local Hölder-type continuity condition.
    Examples are viscous regularisations of equations arising in elasticity.
    For a full discretisation combining a modification of the Stürmer-Verlet method with an inner approximation scheme, weak convergence of piecewise polynomial prolongations of the discrete solutions are proven. These results also imply the existence of a weak solution.
    For the time discretisation, also variable time grids are allowed as long as the deviation from equidistance is not too large.
    A crucial step in the convergence proof is the equivalence with an integro-differential equation of parabolic type.
    In the case of non-monotone perturbations, a priori estimates in fractional Sobolev-Slobodetskii spaces are a prerequisite for the necessary compactness argument.
    This is joint work with Mechthild Thalhammer (Innsbruck, Austria).

  • Boris Andreianov (Besançon): A one dimensional hyperbolic particle-fluid interaction model, theory and numerical approximation
    18.10.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: D'Alambert paradox states that, if the fluid viscosity is neglected, the resulting force of the fluid action on an immersed moving solid is zero. In other words, planes could not fly if the air viscosity was totally neglected ...
    In this talk we present a simple ''particle-in-Burgers'' model combining Burgers equation without viscosity and a viscous interaction prenomenon between the fluid and a point particle. The fluid equation becomes u_t + ( (u^2)/2 )_x = -λ (u-h'(t)) δ_0(x-h(t)) where x=h(t) is the particle path, and δ_0 is the Dirac-δ. The equation is coupled to an evolution equation for the particle path h(⋅); the resulting force on the particle is proportional to the jump of the normal fluxes of the fluid across the particle path, and the whole model conserves the quantity of movement.
    We study well-posedness and numerical approximation of the coupled problem by (as simple as possible) finite volume schemes. Analysis tools have much in common with the case of conservation laws with discontinuous flux.
    Joint work with F. Lagoutiere, N. Seguin and T. Takahashi.

  • Rajesh Kumar (Magdeburg): Convergence analysis of a finite volume scheme for solving non-linear aggregation-breakage equations
    20.09.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: In this talk I will discuss the stability and convergence analysis of a finite volume scheme for solving aggregation-breakage equation which is a non-linear integropartial differential equation.
    First we rewrite this equation in conservative form and then we apply the well known finite volume method. By showing Lipschitz continuity of the numerical fluxes we found that the scheme is second order convergent independently of the meshes for pure breakage problem while for pure aggregation, due to non-linearity, it shows second order convergent only on a uniform and non-uniform smooth meshes. Furthermore, it gives first order convergence on a non-uniform random grid. Finally, for the coupled problem as well, a second order of convergence is shown on uniform and non-uniform smooth meshes whereas first order convergence is obtained on random grid.
    The mathematical results of convergence analysis are also validated numerically.

  • Hagen Eichel (Magdeburg): Supercloseness und Superkonvergenz stabilisierter Finite-Elemente-Diskretisierungen niedriger Ordnung des Stokes-Problems
    20.09.2010, 14:15, V5-148, Oberseminar Numerik
    Abstract: Der Vortrag handelt von Supercloseness und Superkonvergenz stabilisierter Finite-Elemente-Methoden angewandt auf das Stokes-Problem. Es werden sowohl konsistente residuenbasierte Stabilisierungsmethoden, als auch inkonsistente Stabilisierungstypen, basierend auf lokaler Projektion, betrachtet. Weiterhin wird die Supercloseness des Linearteils der MINI-Element-Lösung gezeigt. Die Resultate über Supercloseness werden für Dreieckselemente, sowie achsenparallele Rechtecke und Quader hergeleitet, allerdings auch Erweiterungen auf allgemeine Gitter diskutiert. Durch einen geeigneten Post-Prozess können dann Superkonvergenz-Resultate erzielt werden. Anschließend werden numerische Berechnungen zur Unterstützung der theoretischen Betrachtung präsentiert.

  • Eskil Hansen (Lund): Time stepping schemes for nonlinear parabolic problems and a theorem by Brezis and Pazy
    16.08.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: There is a rich theory describing the approximation of nonlinear semigroups. At its core one finds the results by Brezis and Pazy, who generalize the classical linear results of Trotter and Chernoff. Even though the theory was derived in the early seventies, it is virtually unknown within the numerical community. The aim of this talk is therefore to illustrate how this nonlinear theory can be used as a corner stone when deriving convergence for time stepping schemes applied to fully nonlinear parabolic equations. In particular, we will illustrate our framework by deriving the convergence for splitting schemes and DIRK methods under minimal regularity assumptions.

  • Mechthild Thalhammer (Innsbruck): Exponential operator splitting methods for nonlinear evolutionary problems involving critical parameters
    02.08.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: In this talk, the error behaviour of exponential operator splitting methods for nonlinear evolutionary problems is investigated. In particular, an exact local error representation that is suitable in the presence of critical parameters is deduced. Essential tools in the theoretical analysis including time-dependent nonlinear Schrödinger equations in the semi-classical regime as well as parabolic initial-boundary value problems with high spatial gradients are an abstract formulation of differential equations on function spaces and the formal calculus of Lie-derivatives. The general mechanism is exposed on the basis of the least technical example method, the first-order Lie-Trotter splitting. The conclusion that exponential operator splitting methods are favourable for the time-integration of nonlinear Schrödinger equations in the semi-classical regime with Wentzel-Kramers-Brillouin initial condition under the time stepsize restriction h = O(p√{ε}), where 0 < ε < < 1 denotes the critical parameter and p the order of the splitting method, is confirmed by a numerical example for the time-dependent Gross-Pitaevskii equation.

  • Yuri Latushkin (Columbia, Missouri): Birman-Schwinger operators and the Evans function
    19.07.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: This is a review of some recent work related to the spectral theory of the Birman-Schwinger type integral operators familiar from quantum mechanics, and the Evans function, a popular tool in stability analysis of traveling waves. Some formulas are given relating the Evans function and its derivative and the modified Fredholm determinants of the respective Birman-Schwinger operators.

  • Günter M. Ziegler (TU Berlin): Ein scharfer gefärbter Tverberg-Satz
    15.07.2010, 16:15, V3-201, Mathematisches Kolloquium
    Abstract: Im Herbst 1964 saß der junge norwegische Mathe matiker Helge Tverberg in einem Hotelzimmer in Manchester, fror, und bewies ein bemerkenswertes Resultat: Wenn man 3r-2 Punkte in der Ebene hat, so kann man diese in r Gruppen von höchstens drei Punkten aufteilen, so dass die r dadurch bestimmten Dreiecke, Strecken und Punkte einen gemeinsamen Schnittpunkt haben. Ein Punkt weniger reicht nicht. Eine d-dimensionale Version des Satzes, mit (d+1)(r-1)+1 Punkten, hat Tverberg gleich mitbewiesen.
    1992 haben dann Vrecica und Zivaljevic einen "gefärbten Tverberg-Satz" präsentiert. Für den Beweis wurden elegante topologische Methoden und kombinatorische Strukturen verwendet, aber das Resultat war nicht scharf - Vrecica und Zivaljevic brauchten mehr Punkte als erwartet. Jetzt gibt es eine überraschende neue, scharfe "gefärbte" Version des ursprünglichen Satzes von Tverberg, neue Beweismethoden kommen zum Einsatz - es gibt Fortschritt! Darüber will ich berichten.
    (Gemeinsame Arbeit mit Pavle V. M. Blagojevic und Benjamin Matschke)

  • Alexander Ostermann (Innsbruck): Numerical analysis of operator splitting methods
    12.07.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: Splitting methods form a large class of competitive time discretisations of evolution equations. The reason for their frequent use is that the splitting procedure yields time stepping schemes which dramatically reduce the required computational effort, compared to schemes based on the full vector field.
    After a brief introduction to the concept of splitting and the non-stiff convergence theory, we concentrate on problems with unbounded operators. It turns out that the non-stiff order conditions are sufficient to get optimal convergence orders for exponential splitting methods in the stiff case. We discuss analytic frameworks for proving (optimal) convergence results, and we introduce a new setting that is applicable for a wide variety of linear equations and their dimension splittings. In particular, we analyse parabolic problems with homogeneous Dirichlet or Neumann boundary conditions on bounded domains.
    We further discuss a new class of splitting methods of orders up to fourteen based on complex coefficients. These results resolve the open question whether there exist splitting schemes with convergence rates greater than two in the context of analytic semigroups. As a concrete application we consider once more parabolic equations and their dimension splittings. The sharpness of our theoretical error bounds is illustrated by numerical experiments.

  • Caren Tischendorf (Köln): Solution Approaches for Abstract Differential-Algebraic Equations
    05.07.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: The simulation of complex systems describing different physical effects becomes more and more of interest in various applications, for instance, in chip design, in structural mechanics, in biomechanics and in medicine. The modeling of complex processes often lead to coupled systems that are composed of ordinary differential equations (ODEs), differential-algebraic equations (DAEs) and partial differential equations (PDEs).
    Such coupled systems can be regarded in the general framework of abstract differential-algebraic equations of the form
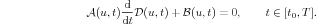
    tischendorf1
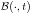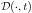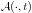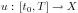    This equation is to be understood as an operator equation with operators tischendorf2, tischendorf3 and tischendorf4 acting in real Hilbert spaces where tischendorf5 is the solution belonging to a problem adapted space.
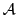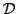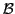    If the Hilbert spaces are chosen to be the finite dimensional space Rm, then we obtain a differential-algebraic equation. Choosing tischendorf6 and tischendorf7 as the natural embedding operators, we obtain an evolution equation. If, additionally, tischendorf8 is a second-degree differential operator in space, it leads to a parabolic differential equation. For elliptic differential equations, the operators tischendorf6 and tischendorf7 are identically zero.
    For most coupled systems, the operators tischendorf6 and tischendorf7 are neither identically zero nor invertible on the time interval [t0,T]. A general theory of abstract differential-algebraic equations (ADAEs) does not exist and can not be expected to be given considering alone the complexity of problems simulating partial differential equations. However, special classes of ADAEs have recently been successfully analyzed and simulated.
    In particular, we discuss solvability and perturbation results via two different approaches. The first one addresses linear ADAEs with constant coefficients using Laplace transformation. The second one handles linear ADAEs with monotone, time dependent coefficients by a Galerkin approach.

  • Christian Kuehn (Cornell):
    14.06.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: We start with an introduction to fast-slow systems. The geometric viewpoint of the theory will be emphasized. Then we discuss the three-dimensional FitzHugh-Nagumo (FHN) equation and its bifurcations. The singular limit bifurcation diagram of the FHN equation will be derived. The computation and interaction of different types of invariant manifolds will be emphasized to explain the dynamics. We shall also briefly look at mixed-mode oscillations (MMOs) in the FHN equation and more general fast-slow system.

  • Dimitri Puhst (TU Berlin): Fractional derivatives and their applications
    11.06.2010, 14:15, V5-148, Oberseminar Numerik

  • Jens Rademacher (CWI Amsterdam): Mechanisms of semi-strong interaction in multiscale reaction diffusion systems
    07.06.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: In spatial multiscale reaction diffusion systems where some diffusion lengths are much shorter than the rest, interfaces can form where only the components with the short scale localise. The interaction between such interfaces is called semi-strong as it is driven by the nonlocalised components. Cases where the interface motion is of the order of the square of the short diffusion lengths ('second order') have been studied over the past decade. By formal expansions and numerical studies we show that the interaction strength can also be of the same order as the short diffusion length ('first order').
    We illustrate these mechanisms in the Schnakenberg model and investigate interaction manifolds and their stability. Taking a model independent point of view, starting only from a dichotomy in diffusion lengths, characteristic equations of motion of interfaces for first and second order semi-strong interaction can be derived. For first order pulse interaction with a single long diffusion length and under certain natural assumptions several explicit Lyapunov-functionals such as the largest interpulse distance are found.
    This is partly joint work with J. Ehrt and M. Wolfrum (WIAS, Berlin).

  • Mario Botsch (Bielefeld): Polyhedral Finite Elements
    31.05.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: Finite element simulations of deformable objects are typically based on spatial discretizations using either tetrahedral or hexahedral elements. This allows for simple and efficient computations, but in turn requires complicated remeshing in case of topological changes or adaptive simulations. In this talk I will show how arbitrary polyhedral elements can be used in FEM simulations, thereby avoiding the need for remeshing (and thus simplifying) adaptive refinement, interactive cutting, and fracturing of the simulation domain.

  • Rolf Dieter Grigorieff (TU Berlin): Qualokation bei periodischen Pseudo-Differentialoperatoren
    03.05.2010, 16:15, V5-148, Oberseminar Numerik
    Abstract: Qualokation bezeichnet ein auf I. Sloan zurückgehendes Diskretisierungsverfahren, das zwischen dem Kollokations- und dem Petrov-Galerkin-Verfahren angesiedelt ist. Der Vortrag handelt von der Konvergenzanalyse des Verfahrens angewandt auf periodische Pseudo-Differentialoperatoren unter Verwendung von Splines mit mehrfachen Knoten als Ansatz- und Testraum. Eine Grundlage dafür sind Approximationseigenschaften der Splineräume, die ebenfalls vorgestellt werden. Besondere Aufmerksamkeit verdient die Bestimmung von Bedingungen an die Parameterwahl des Verfahrens, mit denen eine zusätzliche Konvergenzordnung einhergeht.

  • Jussi Behrndt (TU Berlin): Spektraleigenschaften einer Klasse elliptischer Differentialoperatoren auf beschraenkten und unbeschraenkten Gebieten
    22.04.2010, 17:15, V3-201, Mathematisches Kolloquium
    Abstract: In this lecture we consider a formally symmetric second order elliptic differential expression L on a bounded or unbounded domain Ω with smooth boundary ∂Ω. Our aim is to describe the spectral properties of a family of selfadjoint realizations of L in L2(Ω) with nonlocal boundary conditions on ∂Ω. For this we apply boundary triplet and Dirichlet-to-Neumann techniques, as well as general perturbation methods from abstract operator theory.

  • Mechthild Thalhammer (Innsbruck): High-order time-splitting spectral methods for nonlinear Schrödinger equations
    22.02.2010, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk, I will address the issue of efficient numerical methods for the time integration of nonlinear Schrödinger equations. As model problems, I will consider systems of coupled Gross-Pitaevskii equations that arise in quantum physics for the description of multi-component Bose-Einstein condensates. My intention is to study the quantitative and qualitative behaviour of high-accuracy discretisations that rely on time-splitting Fourier and Hermite spectral methods. In particular, this includes a stability and convergence analysis of high-order exponential operator splitting methods for evolutionary Schrödinger equations. Numerical examples illustrate the theoretical results.

  • Aneta Wróblewska (Warsaw): Unsteady flows of nonhomogeneous non-Newtonian incompressible fluids with growth conditions in Orlicz spaces
    25.01.2010, 14:15, V5-148, Oberseminar Numerik
    Abstract: Our purpose is to show existence of weak solutions to unsteady flow of non-Newtonian incompressible nonhomogeneous fluids with nonstandard growth conditions of the stress tensor. We are motivated by the fluids of strongly inhomogeneous behavior and characterized by rapid shear thickening. Since we are interested in flows with the rheology more general then power-law-type, we describe the growth conditions with help of general x-dependent convex function and formulate our problem in generalized Orlicz spaces.

  • Jos Gesenhues (Bremen): Das Kuramoto-Modell - Modellierung, Analysis und Simulation
    11.01.2010, 14:15, V5-148, Oberseminar Numerik
    Abstract: Das Kuramoto-Modell ist ein Modell für das Verhalten einer großen Anzahl schwach gekoppelter Oszillatoren. Insbesondere können an ihm Synchronisierungsphänomene untersucht werden. In dieser Arbeit werden sowohl das klassische diskrete Kuramoto-Modell als auch ein kontinuierlicher Ansatz, der auf eine partielle, nichtlineare Integro-Differentialgleichung führt, modelliert und analysiert. Das zentrale Ergebnis der Analyse ist ein kritischer Kopplungswert, ab dem Synchronität auftritt. Dieser wird für beide Modelle in Simulationen bestätigt.

  • David Šiška (London): Finite-Difference Approximations for Normalized Bellman Equations
    11.01.2010, 10:15, U5-133, Oberseminar Numerik
    Abstract: A class of stochastic optimal control problems involving optimal stopping is considered. Methods of Krylov (Appl. Math. Optim. 52(3):365-399, 2005) are adapted to investigate the numerical solutions of the corresponding normalized Bellman equations and to estimate the rate of convergence of finite difference approxi- mations for the optimal reward functions.

  • Christopher Hartleb (TU Ilmenau): Beiträge zu unteren Schranken für die Unabhängigkeitszahl eines Graphen in Termen von Knotenzahl und Kantenzahl
    22.12.2009, 10:15, V4-119, Oberseminar Numerik

  • Volker Mehrmann (TU Berlin / MATHEON): Theory and numerical methods for the stability analysis of differential algebraic systems
    14.12.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: Lyapunov and exponential dichotomy spectral theory is extended from ordinary differential equations (ODEs) to nonautonomous differential-algebraic equations (DAEs). By using orthogonal changes of variables, the original DAE system is transformed into appropriate condensed forms, for which concepts such as Lyapunov exponents, Bohl exponents, exponential dichotomy and spectral intervals of various kinds can be analyzed via the resulting underlying ODE. Some essential differences between the spectral theory for ODEs and that for DAEs are pointed out. It is also discussed how numerical methods for computing the spectral intervals associated with Lyapunov and Sacker-Sell (exponential dichotomy) can be extended from those methods proposed for ODEs. Some numerical examples are presented to illustrate the theoretical results.

  • Arjen Doelmann (Leiden): Busse balloons and Hopf dances, or: Bifurcations of Spatially Periodic Patterns
    07.12.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk we propose to study generic aspects of the Busse balloon associated to spatially periodic patterns in reaction-diffusion equations. The Busse balloon -- named after the physicist Friedrich Busse -- is defined as the region in (wave number, parameter space) for which stable periodic patterns exist; the boundary of the Busse balloon is determined by bifurcations/destabilizations. After a general introduction, in which we interpret the Turing bifurcation and the associated side band instability mechanism, as a well-studied and well-understood generic aspect of the Busse balloon, we introduce a novel destabilization mechanism for reversible spatially periodic patterns. This Hopf dance mechanism occurs for long wavelength patterns near the homoclinic tip of a Busse balloon. Here, the boundary of the Busse balloon locally has a fine-structure of two intertwining ?dancing? Hopf destabilization curves (or manifolds) that limit on the Hopf bifurcation value of a homoclinic limit pulse.

  • Thorsten Hüls: On r-periodic orbits of k-periodic maps
    30.11.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk, we analyze r-periodic orbits of k-periodic difference equations, i.e.
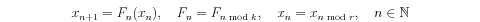
    huels09
    and their stability. We discuss that, depending on the values of r and k, such orbits generically only occur in finite dimensional systems that depend on sufficiently many parameters, i.e. they have a large codimension in the sense of bifurcation theory. As an example, we consider the periodically forced Beverton-Holt model, for which explicit formulas for the globally attracting periodic orbit, having the minimal period k=r, can be derived. When r factors k the Beverton-Holt model with two time-variant parameters is an example that can be studied explicitly and that exhibits globally attracting r-periodic orbits. For arbitrarily chosen periods r and k, we develop an algorithm for the numerical approximation of an r-periodic orbit and of the associated parameter set, for which this orbit exists. We apply the algorithm to the generalized Beverton-Holt and another example that exhibits periodic orbits with r and k relatively prime.

  • Georgy Kitavtsev (WIAS Berlin): Reduced ODE models describing coarsening dynamics of slipping droplets
    23.11.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: In this talk the topic of reduced ODE models corresponding to a family of one-dimensional lubrication equations derived by Münch et al. 06' is addressed. This family describes the dewetting process of nanoscopic thin liquid films on hydrophobized polymer substrates due to the presence of several intermolecular forces and takes account of different ranges of slip-lengths at the polymer substrate interface. Reduced ODE models derived from underlying lubrication equations allow for an efficient analytical and numerical investigation of the latest stage of the dewetting process: coarsening dynamics of the remaining droplets. We first give an asymptotical derivation of these models and use them to investigate the influence of slip-length on the coarsening dynamics. In a so called strong-slip case we find a unique critical slip-length at which the direction for migration of droplets changes. In the second part of the talk we present a new geometric approach which can be used for an alternative derivation and justification of above reduced ODE models and is based on a center-manifold reduction recently applied by Mielke and Zelik 08' to a certain class of semilinear parabolic equations. One of the main problems for a rigorous justification of this approach is investigation of the spectrum of a lubrication equation linearized at the stationary solution, which describes physically a single droplet. The corresponding eigenvalue problem turns out to be a singularly perturbed one with respect to a small parameter ε tending to zero. For this problem we show existence of an ε-dependent spectral gap between a unique exponentially small eigenvalue and the rest of the spectrum.

  • Sergei Pilyugin (St. Petersburg): Lipschitz shadowing property
    09.11.2009, 14:15, V5-148, Oberseminar Numerik

  • Dario Götz (TU Berlin): Existenz von schwachen Lösungen und Zeitdiskretisierung der Bewegungsgleichung verallgemeinerter nicht-Newtonscher Fluide
    19.10.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: Nicht-Newtonsche Fluide verhalten sich, meist aufgrund von zugrundeliegenden Mikrostrukturen, anders, als man es von gewöhnlichen Flüssigkeiten erwartet; so zum Beispiel Blut, Lava, Farbe, Tomatenketchup, Polymere, Emulsionen oder Suspensionen.
    Im Vortrag untersuchen wir die schwache Lösbarkeit der instationären Bewegungsgleichung für inkompressible Fluide mit scherratenabhängiger Viskosität, wobei wir für den Spannungstensor eine p-Struktur voraussetzen. Im Fall 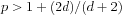goetz1 kann die schwache Lösbarkeit mithilfe der Theorie monotoner Operatoren gezeigt werden. Mathematisch anspruchsvoller ist der Fall p < 2, der hier behandelt werden soll. 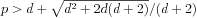Ziel ist es, die schwache Lösbarkeit des Problems für alle goetz2 zu zeigen. Ein Problem, das sich dabei ergibt, ist die fehlende Regularität der zeitlichen Ableitung der Lösung.
    Die Beweisidee beruht auf einer Zeitdiskretisierung durch ein implizites Euler-Verfahren. Mithilfe der sogenannten parabolischen Lipschitz-Truncation-Methode und geeigneten Regularitätsaussagen in gebrochenen Sobolew-Räumen wird das Problem der fehlenden Regularität der zeitlichen Ableitung gelöst. Damit geht eine Repräsentation des in der schwachen Formulierung verschwindenden Druckes einher, die essenziell für diese Beweisidee ist.

  • Arnulf Jentzen (Frankfurt): Taylor expansions for stochastic partial differential equations
    24.07.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: Taylor expansions of stochastic partial differential equations (SPDEs) of evolutionary type and their first applications to numerical analysis are presented. The key instruments for deriving such Taylor expansions are the semigroup approach, i.e. to understand the SPDE as a mild integral equation, and an appropriate recursion technique.

  • David Speer (Bielefeld): Directing Brownian Motion in Periodic Potentials
    03.07.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: We consider a single Brownian particle subjected to periodic and symmetric potentials. Directed particle transport can be achieved only by breaking symmetry, such as applying a constant force. Usually, particle transport is in the direction of that force, in line with the second law of thermodynamics. In non-equilibrium, this behaviour may be drastically different due to a subtle interplay of deterministic chaos, symmetry and stochastic forces. This may be exploited to achieve almost complete control of transport direction, even transport directly against that force (negative absolute mobility) [1]. Recently, the effect was observed experimentally for Josephson junctions [2].
    [1] D. Speer et al., Europhys. Lett. 79, 10005 (2007), D Speer et al., Phys. Rev. Lett. 102, 124101 (2009)
    [2] J. Nagel et al., Phys. Rev. Lett. 100, 217001 (2008)

  • Lutz Angermann (Clausthal): Rosenbrock-Verfahren fü PDAEs
    19.06.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: Die mathematische Modellierung zahlreicher Probleme aus Naturwissenschaft, Technik, Medizin etc. fürt auf (i. Allg. nichtlineare) Gleichungssysteme, die aus gekoppelten Gleichungen unterschiedlichen Typs bestehen, zum Beispiel aus parabolischen, elliptischen, gewöhnlichen Differentialgleichungen und aus algebraischen Gleichungen. Derartige Systeme heißen partielle differentiell-algebraische Gleichungen (PDA-Systeme, engl.: partial differential algebraic equations, PDAEs).
    Die Entwicklung numerischer Approximationsverfahren für die Lösung dieser Systeme mittels der vertikalen Linienmethode (Diskretisierung zuerst im Raum) wirft bei dem Versuch der Übertragung bekannter, für differentiell-algebraische Gleichungen moderater Größe entworfener Methoden auf die entstehenden (gewöhnlichen) differentiell-algebraischen Gleichungen (sog. MOL-DAEs) eine Reihe zusätzlicher oder neuer Fragestellungen auf, die - einschließlich entsprechender Lösungsansätze -- im Vortrag erörtert werden sollen.

  • Mario Ohlberger (Münster): Reduzierte Basis Techniken für parametrisierte nichtlineare Evolutionsgleichungen
    15.05.2009, 14:15, V5-148, Oberseminar Numerik
    Abstract: In diesem Vortrag werden wir die Reduzierte Basis Methode zur effizienten Lösung parametrisierter Evolutionsgleichungen vorstellen. Die Methode erlaubt eine offline/online Zerlegung des Lösungsprozesses. Zunächst wird in einer Offline-Phase mit Hilfe von Finite Elemente oder Finite Volumen Verfahren ein reduzierter Basisraum generiert, der auf die konkrete Problemstellung angepasst ist. In einer Online-Phase können dann - unabhängig von der Komplexität der zugrundeliegenden Finite Elemente oder Finite Volumen Verfahren - sehr schnell Simulationsergebnisse für beliebige Parametervariationen berechnet werden.

  • Hans-Georg Purwins (Münster): Lokalisierte Lösungen der erweiterten FitzHugh-Nagumo-Gleichung
    07.05.2009, 12:30, V3-201, Kolloquium FSPM
    Abstract: Selbstorganisierte dissipative Strukturen sind in Natur und Technik weit verbreitet und nicht wenige Wissenschaftler sind der Ansicht, dass deren Verstîndnis und Anwendung eine der ganz großen Herausforderungen der modernen Naturwissenschaften darstellen. Der vorliegende Vortrag beschäftigt sich mit derartigen Strukturen in der Form von solitären lokalisierten Spots, die auch „Dissipative Solitonen” (DSen) genannt werden. Diese Objekte zeigen in vieler Hinsicht teilchenhaftes Verhalten und werden sowohl experimentell als auch als Lösungen von Reaktions-Diffusions-Systemen vom FitzHugh-Nagumo-Typ beobachtet.
    Im ersten Teil des Vortrags wird an Hand von experimentellen elektrischen Transportsystemen dargelegt, dass DSen z.B. als stationäre und laufende isolierte Pulse, als stationäre, laufende und rotierende „Moleküle” und als „kristalline”, „flüssige” und „gasförmige” Vielteilchensysteme auftreten. Die dabei entdeckten Wechselwirkungsphänomen umfassen sowohl Streuung und Clusterbildung als auch Generation und Annihilation. Numerische Untersuchungen zeigen, dass sich alle experimentellen Beobachtungen qualitativ durch die verallgemeinerte FitzHugh-Nagumo- Gleichung beschreiben lassen. Es erweist sich, dass diese Gleichung als eine Art „Normalform” für eine grüßere Universalitätsklasse DSen tragender Systeme betrachtet werden kann.
    Im zweiten Teil des Vortrags wird besprochen, wie sich unter bestimmten Voraussetzungen aus der verallgemeinerten FitzHugh-Nagumo-Gleichung Teilchengleichungen ableiten lassen, die das dynamische Verhalten schwach wechselwirkender DSen sehr gut beschreiben.

  • Christian Wieners (Karlsruhe): Effiziente numerische Methoden in der Elasto-Plastizität
    11.07.2008, 14:15, V2-210, Oberseminar Numerik
    Abstract: Im Vortrag wird zunächst das klassische Modell der Prandtl-Reuß-Plastizität erläutert, und es werden effiziente numerische Methoden zur Lösung des diskreten Finite-Elemente-Problems vorgestellt. Da diese Probleme in der Regel schlecht konditioniert oder sogar schlecht gestellt sind, werden robuste Verfahren benötigt. Insbesondere werden moderne Methoden diskutiert, die auf Konzepten der Optimierung beruhen (nicht-glatte Newton-Verfahren, SQP-Verfahren).
    Im zweiten Teil des Vortrags werden neuere Anwendungen vorgestellt. Die klassischen Modelle lassen sich unter Zunahme von infinitesimalen Rotationen oder Gradienten der plastischen Verzerrungen regularisieren (Zusammenarbeit mit P. Neff, Darmstadt). Es wird gezeigt, dass sich die numerischen Lösungsverfahren auf die erweiterten Modelle übertragen lassen. Schließlich wird die Effizienz der Methoden an einer parallelen Simulation eines elasto--plastischen bodenmechanischen Modells demonstriert (Zusammenarbeit mit W. Ehlers, Stuttgart).

  • Peter Giesl (Sussex): Determination of the Basin of Attraction of Equilibria and Periodic Orbits
    10.07.2008, 14:15, V2-210, Oberseminar Numerik
    Abstract: The basin of attraction of equilibria or periodic orbits of an autonomous ODE can be determined through sublevel sets of a Lyapunov function. To construct such a Lyapunov function, i.e. a scalar-valued function which is decreasing along solutions of the ODE, a linear PDE is solved approximately using Radial Basis Functions. Error estimates ensure that the approximation itself is a Lyapunov function.
    For the construction of a Lyapunov function it is necessary to know the position of the equilibrium or periodic orbit. A different method to analyse the basin of attraction of a periodic orbit without knowledge of its position is Borg's criterion. The sufficiency and necessity of this criterion in different settings will be discussed.

  • Fritz Colonius (Augsburg): Near Invariance and Local Transience for Perturbed Systems
    27.06.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: Nearly invariant subsets of the state space of a dynamical system are subsets which can only be left after long time. For families of random diffeomorphisms one can characterize these subsets via an associated discrete-time control system and, also using the Perron-Frobenius operator, one can show that the exit times are positive and polynomially unbounded.

  • Günther Grün (Erlangen): Energiemethoden zur Analyse von Benetzungsph"anomenen
    20.06.2008, 14:15, V5-148, Oberseminar Numerik

  • Jens Lorenz (Albuquerque, New Mexico): The Brenner-Klimontovich Modifications of the Navier-Stokes-Fourier System
    16.06.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: The classical Navier-Stokes-Fourier equations for heat conducting compressible flows form a coupled hyperbolic-parabolic system. The system has been criticized, on principle grounds, as being inconsistent with non-equilibrium thermodynamics. In this talk I consider modified systems, suggested by Brenner and Klimontovich, which are essentially parabolic. The modified systems distinguish between a mass velocity and a volume velocity.
    I also show some crude numerical results.

  • Gerhard Starke (Hannover): Eine adaptive gemischte Finite-Elemente-Methode für elastische Kontaktprobleme
    23.05.2008, 14:15, V5-148, Oberseminar Numerik

  • Wolf-Jürgen Beyn: Localization and continuation of nonlinear eigenvalues
    16.05.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: Nonlinear eigenvalue problems are ubiquitous in the stability analysis of nonlinear systems, such as vibrating systems or systems with delay. Numerical discretizations then lead to large and sparse parameterized nonlinear eigenvalue problems
    beyn1
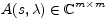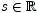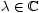    where the matrix family beyn2 depends smoothly on the real parameter beyn3 and analytically on the eigenvalue parameter beyn4. We aim at an algorithm that detects a small swarm of eigenvalues λ within a prescribed complex domain and that continues the swarm with respect to the parameter s.
    A new localization procedure is presented that determines the eigenvalues (and eigenvectors) in the interior of a smooth contour of the complex plane. The method builds on Cauchy's integral formula and on a theorem of Keldysh. Then we discuss a continuation method that pursues the swarm of eigenvalues with the parameter and that deflates and inflates the swarm when collisions with outside eigenvalues occur.

  • Tycho van Noorden (Eindhoven): Crystal dissolution and precipitation in porous media: formal homogenization and numerical experiments
    09.05.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: We investigate a two-dimensional micro-scale model for crystal dissolution and precipitation in a porous medium. The model contains a free boundary and allows for changes in the pore volume. Using a level-set formulation of the free boundary, we apply a formal homogenization procedure to obtain upscaled equations. For general micro--scale geometries, the homogenized model that we obtain falls in the class of distributed microstructure models. For circular initial inclusions the distributed microstructure model reduces to system of partial differential equations coupled with an ordinary differential equation. In order to investigate how well the upscaled equations describe the behavior of the micro-scale model, we perform numerical computations for a test problem.

  • Christof Eck (Bielefeld): Asymptotik und numerische Approximation von Phasenfeldmodellen
    18.04.2008, 14:15, V5-148, Oberseminar Numerik

  • Etienne Emmrich (TU Berlin): Analysis der Zeitdiskretisierung von Evolutionsgleichungen mit monotonem Operator durch die BDF 2
    20.02.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: Zeitabhängige Prozesse in Natur und Technik önnen oft durch das Anfangswertproblem für eine Evolutionsgleichung rster Ordnung mit monotonem Hauptteil modelliert werden. Zur Zeitdiskretisierung stehen eine Vielzahl von Methoden zur Verfügung, wobei sich die zweischrittige Formel der rückwärtigen Differenzen (Backward differentiation formula 2) durch ihre Eigenschaften auszeichnet.
    Der Vortrag gibt zunächst einen Überblick über bekannte Resultate für lineare und semilineare Probleme bei äquidistantem als auch variablem Zeitgitter. Alsdann werden Wohlgestelltheit, A-priori-Abschätzungen, Konvergenz stückweise polynomialer Prolongationen, Stabilität und Fehlerabschätzungen für den Fall konstanter Zeitschrittweite bei Anwendung auf eine Evolutionsgleichung mit monotonem Operator und verstärkt stetiger Störung studiert. Als fundamental stellt sich dabei eine algebraische Identität heraus, die zugleich die G-Stabilität des Verfahrens nach sich zieht. Schließlich wird der Fall variabler Zeitschritte diskutiert.

  • Peter Benner (TU Chemnitz): Control-oriented model reduction for parabolic systems
    25.01.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: We will discuss model reduction techniques for the control of dynamical processes described by parabolic partial differential equations from a system-theoretic point of view.
    The methods considered here are based on spatial semi-discretization of the PDE followed by balanced truncation techniques applied to the resulting large-scale system of ordinary differential equations. Several choices of the system Gramians that are used for balancing will be presented.
    We will discuss open-loop and closed-loop techniques that allow to preserve system properties important for controller design. Furthermore we will discuss an error estimate based on a combination of FEM and model reduction error bounds. We will also discuss how the state of the full-order system can be recovered from the reduced-order model. Several numerical examples will be used to demonstrate the proposed model reduction techniques.

  • Barnabas Garay (TU Budapest): Chaos Detection by Computer
    21.01.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: We report on experiences with an adaptive subdivision method supported by interval arithmetic that enables us to prove subset relations for certain mappings associated with the dynamics and thus to check certain sufficient conditions for chaotic behaviour in a rigorous way.
    Our proof of the underlying abstract theorem avoids of referring to any results of applied algebraic topology and relies only on the Brouwer fixed point theorem.
    The second novelty is that the process of gaining the subset relations to be checked is, to a large extent, also automatized. The promising subset relations come from solving a constrained optimization problem via the penalty function approach.
    Abstract results and computational methods are demonstrated by finding planar subsets with chaotic behaviour for iterates of the classical Henon mapping as well as for the time-T-map of the solution operator to a damped pendulum equation with T-periodic forcing.

  • Alexander Dressel (Stuttgart): Existence, uniqueness and time-asymptotic behaviour of weak solutions for a viscoelastic two-phase model with nonlocal capillarity
    11.01.2008, 14:15, V5-148, Oberseminar Numerik
    Abstract: The aim of this talk is to study the existence, uniqueness and time-asymptotic behaviour of solutions of an initial-boundary value for a viscoelastic two-phase material with capillarity in one space dimension. Therein, the capillarity is modelled via a nonlocal interaction potential. The existence proof relies on uniform energy estimates for a family of difference approximations: with these estimates at hand we show the existence of a global weak solution. By means of a nontrivial variant of existing arguments in the literature (the so-called "Andrews-trick") , uniqueness and further regularity are proven.Then, based on the existence and regularity results, we prove the time-asymptotic convergence of the strain-velocity field.

  • Anton Arnold (TU Wien): Offene Randbedingungen für Wellenausbreitungsprobleme in unbeschränkten Gebieten
    19.12.2007, 15:00, V5-148, Oberseminar Numerik
    Abstract: Partielle Differentialgleichungen auf unbeschränkten Gebieten treten ganz natürlich in akustischen, quantenmechanischen und strömungsmechanischen Problemen auf. Die numerische Simulation muß daher meist auf ein endliches Teilgebiet beschränkt werden - durch die Einführung von (künstlichen) absorbierenden Randbedingungen.
    Im Vortrag werden wir einen Überblick über solche Strategien geben und insbes. Anwendungen auf die zeitabhängige Schrödinger Gleichung in 1D und 2D (Streifen und Kreisgeometrie) diskutieren.

  • Heinrich Voß (TU Hamburg-Harburg): Numerical methods for sparse nonlinear eigenvalue problems
    14.12.2007, 14:15, V5-148, Oberseminar Numerik
    Abstract: We consider the nonlinear eigenvalue problem
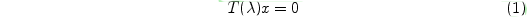
    voss1
    where 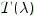voss2 is a family of sparse matrices. Problems of this type arise in damped vibrations of structures, conservative gyroscopic systems, lateral buckling problems, fluid-solid vibrations, and the electronic behaviour of quantum dot heterostructures, to name just a few.
    We discuss iterative projection methods of Jacobi-Davidson and Arnoldi type which are particularly efficient if the eigenvalues of (1) satisfy a minmax property. Moreover, we present a variant of the automated multi-level substructuring for nonlinear problems.

  • Olaf Steinbach (TU Graz): Boundary Integral Equations: Analysis and Applications
    07.12.2007, 14:15, V5-148, Oberseminar Numerik

  • Kathrin Schreiber (TU Berlin): Nonlinear Rayleigh functionals
    23.11.2007, 14:15, V5-148, Oberseminar Numerik
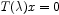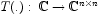    Abstract: After a short introduction on nonlinear eigenvalue problems, defined byschreiber1 where schreiber2 is a matrix-valued mapping, we review Rayleigh quotients for Hermitian and general matrices and introduce appropriate {\em Rayleigh functionals} p(u) and p(u, v) defined by
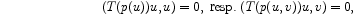
    schreiber3
    for nonlinear eigenvalue problems, where u, v are approximations for right and left eigenvectors. Local existence and uniqueness of p is shown as well as 'stationarity' (technically p is not differentiable). Bounds for the distance of p and the exact eigenvalue are provided, which are of the same order as in the linear case.
    The last part of the presentation includes numerical results, where the emphasis lies on complex symmetric problems, where the application of the symmetric Rayleigh functional gives considerably better results associated with an Jacobi-Davidson type method compared to the standard Jacobi-Davidson method.

  • Helmut Podhaisky (Halle): Zweischritt-Peer-Methoden zur Lösung zeitabhängiger partieller Differentialgleichungen
    19.10.2007, 14:15, V5-148, Oberseminar Numerik
    Abstract: Für die numerische Lösung von Anfangswertaufgaben gibt es zwei populäre Verfahrensklassen: lineare Mehrschrittformeln, z.B. vom BDF-Typ, auf der einen Seite und Runge-Kutta-Verfahren auf der anderen. Vor- und Nachteile sind gut bekannt: Mehrschritt-Verfahren haben einen sehr geringen Aufwand pro Schritt, Runge-Kutta-Verfahren habe exzellente Stabilitätseigenschaften. Kann man die Vorteile kombinieren? Die Antwort ist 'ja' (bzw. 'ja, eventuell'), man muss nur allgemeine lineare Verfahren (engl.: \emph{general linear methods}, GLMs), also mehrstufige Mehrschrittverfahren, betrachten.
    Im Vortrag werden Peer-Methoden vorgestellt, die s Approximationen 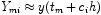podhaisky2, i=1,...,s in einem diagonal impliziten Schema
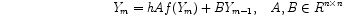
    podhaisky1
    berechnen. Die Ordnungsbedingungen ergeben sich aus Taylorreihenentwicklung. Schwieriger ist, Stabilität, insbesondere A-Stabilität, zu sichern und die verbleibenden freien Parameter so zu optimieren, dass die Methoden robust arbeiten.
    Am Ende des Vortrags werden Peer-Methoden bis zur Ordnung 4 als Zeitintegrationsverfahren im FEM-Code KADOS zur Lösung partieller Differentialgleichungen angewendet.

  • Arnd Scheel (Minnesota): Periodic patterns: perturbation, modulation and bifurcation
    12.10.2007, 14:15, V5-148, Oberseminar Numerik

  • Thorsten Hüls: Numerical approximation of homoclinic trajectories for non-autonomous maps
    09.05.2007, 14:15, V5-148, Oberseminar Numerik
    Abstract: For time-dependent dynamical systems of the form
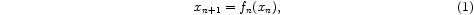
    huels1
    homoclinic trajectories are the non-autonomous analog of homoclinic orbits from the autonomous world.
    More precisely, two trajectories (xn)n ∈ Z, (yn)n ∈ Z of (1) are called homoclinic to each other, if
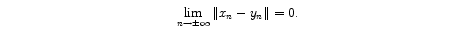
    huels2
    We introduce two boundary value problems, the solution of which yield finite approximations of these trajectories. Under certain dichotomy and transversality assumptions, we prove existence, uniqueness and error estimates. Finally, the method and the error estimates are illustrated by an example.

  • Sergei Pilyugin (St. Petersburg): Dynamics of some mappings determined by piecewise linear functions
    25.04.2007, 14:15, V5-148, Oberseminar Numerik
    Abstract: We study dynamics of multidimensional mappings that are determined by scalar functions. Such mappings arise, for example, when we discretize a semilinear parabolic equation. If the determining scalar function is piecewise-linear (with a finite number of "corner" points), then the dynamics is described by a finite number of parameters, and approaches of "discrete nature" are applicable.

  • Jörg Härterich (FU Berlin): Convergence to Rotating Waves in Spatially Inhomogeneous Balance Laws
    11.04.2007, 14:15, V5-148, Oberseminar Numerik
    Abstract: I will study the long-time behaviour of scalar balance laws where the source term is space-dependent. It turns out that under some assumptions solutions exist which converge to rotating waves. After explaining the proof of this statement I will discuss which role these rotating waves play within the global attractor. In addition, some remarks concerning the effect of small viscosity and the case where the assumptions are violated, will be presented.

  • Daniel Holtz (Bielefeld): Überlappender Schwarz-Algorithmus für nichtlineare Konvektions-Probleme
    20.12.2006, 12:30, V3-201, Oberseminar Numerik
    Abstract: Der Schwarz-Algorithmus wird verwendet, um Randwertprobleme mit Hilfe von Gebietszerlegungen numerisch parallel zu berechnen. Der Vortrag stellt eine Realisierung dieses Algorithmus vor. Im eindimensionalen Fall wird für parabolische nichtlineare Differentialgleichungen Konvergenz des Algorithmus bewiesen und numerisch überprüft. Viele Parameter des Algorithmus sind vom Anwender frei wählbar. Basierend auf der Wahl der Randwerte für die Teilgebiete wird eine Verbesserung des Algorithmus vorgestellt.

  • Marcel Oliver (Bremen): Subgrid closures for passive advection through nonreflecting boundary conditions in Fourier space
    13.12.2006, 14:15, V5-148, Oberseminar Numerik
    Abstract: We consider the evolution of a passive scalar in a shear flow in its representation as a system of lattice differential equations in wave number space. When the velocity field has small support, the interaction in wave number space is local and can be studied in terms of dispersive linear lattice waves. We close the restriction of the system to a finite set of wave numbers by implementing transparent boundary conditions for lattice waves. This closure is studied numerically in terms of energy dissipation rate and energy spectrum, both for a time-independent velocity field and for a time-dependent synthetic velocity field whose Fourier coefficients follow independent Ornstein-Uhlenbeck stochastic processes.

  • Martin Rasmussen (Augsburg): Morse-Zerlegungen nichtautonomer dynamischer Systeme
    06.12.2006, 14:15, V5-148, Oberseminar Numerik
    Abstract: Das globale asymptotische Verhalten dynamischer Systeme auf kompakten metrischen Räumen läßt sich mittels Morse-Zerlegungen beschreiben. Deren Komponenten, die so genannten Morse-Mengen, erhält man als Schnitte von Attraktoren und Repeller. In diesem Vortrag werden spezielle Begriffe von Attraktoren und Repeller für nichtautonome dynamische Systeme eingeführt, die geeignet für eine nichtautonome Verallgemeinerung der Morse-Zerlegungen sind. Die dynamischen Eigenschaften dieser Morse-Zerlegungen werden diskutiert; besonderes Augenmerk wird hierbei auf eindimensionale und lineare Systeme gelegt.

  • Malte Samtenschnieder: Periodische Orbits zeitdiskreter nicht-autonomer dynamischer Systeme und ihre Stabilitätseigenschaften
    08.11.2006, 14:15, U2-205, Oberseminar Numerik
    Abstract: Ausgehend vom autonomen Fall, stehen in diesem Vortrag periodische Orbits nicht-autonomer dynamischer Systeme im Mittelpunkt. Für natürliche Zahlen 2 ≤ r < k betrachten wir - statt für festes F - für eine zeitlich veränderliche k-periodische Funktionenfamilie {Fn}n ∈ Z so genannte r-Zykel cr, für die wir eine Stabilitätsanalyse durchführen. Mit Hilfe eines Satzes, der im nicht-autonomen Fall den Zusammenhang zwischen der Stabilität eines Fixpunkts und der Stabilität eines Zykels herstellt, zeigen wir: Wenn cr für das betrachtete nicht-autonome dynamische System global asymptotisch stabil ist, folgt, dass r ein Teiler von k ist. In dieser speziellen Situation approximieren wir r-periodische Orbits k-periodischer Funktionenfamilien mit Hilfe eines auf einer Fixpunktgleichung basierenden Lösungsverfahrens. Ausgehend vom periodischen Beverton-Holt-Modell und der periodischen Stiletto-Abbildung geben wir numerische Ergebnisse an, deren Stabilität wir ebenfalls untersuchen. Abschließend skizzieren wir, welche Probleme auftreten, wenn wir die Bedingung, dass r ein Teiler von k ist, fallen lassen. Wir begründen, warum wir dann allgemein keine Lösung angeben können.

  • Anke Mayer-Bäse (Florida): Challenges in Computational Intelligence: From Neurodynamics to Medical Imaging
    12.07.2006, 14:15, V5-148, Oberseminar Numerik

  • Clarence Rowley (Princeton): Template-based methods for model reduction and control of systems with symmetry
    05.07.2006, 14:15, V5-148, Oberseminar Numerik

  • Thorsten Hüls: Non-autonomous difference equations and bifurcations
    28.06.2006, 14:15, V5-148, Oberseminar Numerik

  • Janosch Rieger: Numerical grid methods for differential inclusions
    31.05.2006, 14:15, V5-148, Oberseminar Numerik

  • Renate Winkler (HU Berlin): Stochastic DAEs in Circuit Simulation
    24.05.2006, 14:15, V5-148, Oberseminar Numerik

  • Jens Rademacher (WIAS Berlin): Computing absolute and essential spectra using continuation
    17.05.2006, 14:15, V5-148, Oberseminar Numerik

  • Daniel Kressner (TU Berlin): Structured eigenvalue problems
    10.05.2006, 14:15, V5-148, Oberseminar Numerik

  • Vera Thümmler: Wie man wandernde Wellen einfriert,ohne ihre Stabilität zu zerstören
    03.05.2006, 14:15, V5-148, Oberseminar Numerik

  • Alexander Lust: Eine hybride Methode zur Berechnung von Liapunow-Exponenten.
    26.04.2006, 14:15, V5-148, Oberseminar Numerik

  • Sergei Pilyugin (St. Petersburg): Sets of dynamical systems with various limit shadowing properties
    12.04.2006, 14:15, V5-148, Oberseminar Numerik

  • Simon Malham (Edinburgh): Efficient strong integrators for linear stochastic systems
    17.03.2006, 14:15, V5-148, Oberseminar Numerik

  • Sergey Piskarev (Bielefeld, Moskau): Maximal regularity for parabolic and elliptic problems
    25.01.2006, 14:15, V5-148, Oberseminar Numerik

  • Andreas Münch (HU Berlin): Non-classical shock solutions and other issues in thin film problems
    11.01.2006, 14:15, V5-148, Oberseminar Numerik

  • Alexander Dressel (Heidelberg): Existence of smooth shock profiles for hyperbolic balance laws
    14.12.2005, 14:15, V5-148, Oberseminar Numerik

  • Jens Rottmann-Matthes: Spektrale Eigenschaften gemischt hyperbolisch-parabolischer Systeme
    22.07.2005, 14:15, V5-148, Oberseminar Numerik

  • Abigail Wacher (Frankfurt): Lösung partieller Differentialgleichungen mit gewichteten, beweglichen finiten Elementen
    08.06.2005, 14:15, V5-148, Oberseminar Numerik

  • Caren Tischendorf (TU Berlin): Stabilitätserhaltende Integration von DAEs
    02.02.2005, 14:15, V5-148, Oberseminar Numerik

  • Sergey Piskarev (Twente,Moskau): On the approximation of attractors
    26.01.2005, 14:15, V5-148, Oberseminar Numerik
    Abstract: We consider semilinear problems of the form u' = Au + f(u), where A generates an exponentially decaying compact analytic semigroup in a Banach space E and f is globally Lipschitz and bounded map from Eα into E (Eα=D((-A)α) with the graph norm). These assumptions ensure that the problem has a global attractor. Under a very general approximation scheme we prove that the dynamics of such problem behaves upper semicontinuously.
    We also prove that, if all equilibrium solutions of this problem are hyperbolic, then there is an odd number of such equilibrium solutions. Additionally, if we impose that every global solution converges as t → ± ∞, (e.g. gradient semigroups with isolated equilibria), then we prove that under this approximation scheme the attractors also behave lower semicontinuously.
    This general approximation scheme includes finite element method, projection and finite difference methods. The main assumption on the approximation is the compact convergence of resolvents which may be applied to many other problems not related to discretization.

  • Wilhelm Huisinga (FU Berlin): Metastability and Dominant Eigenvalues of Transfer Operators
    25.11.2004, 10:15, W0-135, Seminar GK Strukturbildungsprozesse
    Abstract: There are many problems in physics, chemistry and biology where the length and time scales corresponding to the microscopic descriptions (given in terms of some stochastic or deterministic dynamical system), and the resulting macroscopic effects differ many orders of magnitude. Rather than resolving all microscopic details, often one is interested in characteristic features on a macroscopic level (e.g., phase transitions, conformational changes of bio-molecules, climate changes etc.). In this setting, metastability is important macroscopic characteristic which is related to the long time behavior of the dynamical system. It refers to the property that the dynamics is likely to remain within a certain part of the state space for a long period of time, until it eventually exits and transits to some other part of the state space. In this talk we introduce the concept of metastability in the setting of Markov processes, and prove upper and lower bounds for a decomposition of the state space into metastable subsets in terms of dominant eigenvalues and eigenvectors of a corresponding transfer operator. The bounds are explicitly computable and sharp. The results do not rely on any asymptotic expansions in terms of some smallness parameter, but rather hold for arbitrary transfer operators satisfying a reasonable spectral condition.

  • G. Grammel (TU München): Approximation bei Differentialinklusionen
    24.11.2004, 14:15, V5-148, Oberseminar Numerik

  • Barnabas Garay (TU Budapest): The Miranda approach: a framework for computer-assisted proofs of chaos
    17.11.2004, 14:15, V5-148, Oberseminar Numerik

  • Julia Nolting: Bifurkationen periodischer Orbits und ihre numerische Berechnung
    21.07.2004, 14:15, V5-148, Oberseminar Numerik

  • Stefan Siegmund (Frankfurt/Main): Zeitvariante lineare Systeme
    15.07.2004, 14:15, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse
    Abstract: Will man nichtlineare Phänomene lokal verstehen, so kann dies bestenfalls nur so gut gelingen wie man die lineare Theorie verstanden hat. Das Verhalten einer linearen Differentialgleichung xt = Ax wird vollständig durch die Eigenwerte und Eigenräume der n x n-Matrix A beschrieben. Welche mathematischen Konzepte übernehmen die Rolle der Eigenwerte und Eigenräume, falls A sich durch zufällige, kontrollierte oder allgemeine deterministische Einflüsse zeitlich ändert? Im Vortrag werden die historische Entwicklung über Floquet, Lyapunov, Bohl, Osedelets, Sacker und Sell nachgezeichnet, Beispiele gegeben und Zusammenhänge und aktuelle Resultate beschrieben.

  • Jerrold E. Marsden (CalTech, Pasadena): The Euler-Poincare Equations
    01.07.2004, 17:15, V3-201, Mathematisches Kolloquium
    Abstract: The Euler-Poincare equations were born in 1901 when Poincare made a sweeping generalization of the classical Euler equations for the rigid body and ideal fluids. He did this by formulating the equations on a general Lie algebra, the rigid body being associated with the rotation Lie algebra and fluids with the Lie algebra of divergence free vector fields. Since then, this setting has been used for many other situations, such as the KdV equation, shallow water waves, averaged fluid equations, and the template matching equations of computer vision to name just a few. This talk will give an overview of Euler-Poincare and Lie-Poisson reduction theory (from the tangent and cotangent bundles of a Lie Group to its Lie algebra or dual) and then will focus on the specifics for the case of the algebra of all vector fields. Special singular solutions will be described which generalize the peakon (soliton) solutions of the (Camassa-Holm-Fokas-Fuchsteiner) shallow water equations from one to higher dimensions; the manner in which momentum maps (in the sense of Noether's theorem from mechanics) play an important role in these special singular solutions will be presented. (Joint work with Darryl Holm)

  • Giovanni Samaey (Leuven): Connecting orbits in delay differential equations: computation and application to traveling waves in delay PDEs
    02.06.2004, 14:15, V5-148, Oberseminar Numerik
    Abstract: Connecting orbits in delay differential equations (DDEs) are approximated using projection boundary conditions, which involve the stable and unstable manifolds of a steady state. However, in contrast with ODEs, the stable manifold of a steady state of a DDE is infinite-dimensional. We circumvent this problem by reformulating the end conditions using a special bilinear form. The resulting boundary value problem is solved in the Matlab package DDE-BIFTOOL using a collocation method. We show numerical convergence results in terms of discretization and truncation errors, and compare these to the ODE case.
    Besides their importance for the bifurcation analysis of DDEs, homoclinic and heteroclinic orbits arise naturally when looking for traveling waves ofdelay partial differential equations (delay PDEs). We show that, using DDE-BIFTOOL, we can compute these traveling waves, as well as the rightmost part of their spectrum. The numerical results suggest that the spectral properties of traveling waves in delay PDEs are comparable to properties that were proved by Sandstede for the PDE case.

  • Imre Bozi (Budapest): Multiplicity results for the one-dimensional p-Laplacian
    26.05.2004, 14:15, V5-148, Oberseminar Numerik

  • Bernd Krauskopf (Bristol): The saddle-node Hopf bifurcation with global reinjection
    05.02.2004, 12:30, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse

  • Christian Poetzsche (Augsburg): Nonautonomous Dynamics, Time Scales and Discretization
    10.12.2003, 14:15, V5-148, Oberseminar Numerik

  • Tobias Gayer (Augsburg): Fast-Invarianz bei Diffusionsprozessen und parameterabhängige Kontrollsysteme - Resultate und numerische Methoden
    05.11.2003, 14:15, V5-148, Oberseminar Numerik

  • Nils Wagner (Stuttgart): Über mehrfache Eigenwerte bei parameterabhängigen Polynommatrizen
    29.10.2003, 14:15, V5-148, Oberseminar Numerik

  • Lars Grüne (Bayreuth): Numerics and applications of stochastic optimal control
    28.05.2003, 14:15, V5-148, Oberseminar Numerik

  • Zou Yong-Kui (Changchun): Generalized Hopf bifurcation for non-smooth planar dynamical systems
    21.05.2003, 14:15, V5-148, Oberseminar Numerik

  • Jens Kemper: Attraktoren und invariante Maße in Reaktions-Diffusions-Gleichungen
    29.01.2003, 14:15, V5-148, Oberseminar Numerik

  • Andrei Afendikov (Keldysh Institut): Numerical exterior algebra in spectral problems of stability
    24.10.2002, 12:30, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse
    Abstract: Spectral problems of stability on a finite or infinite interval often lead to stiff problems that are difficult to handle numerically. Using as an example the problem of stability for the pulse solution to the complex Ginzburg-Landau equation it is supposed to demonstrate how classical shooting methods can be transformed to a modern exterior algebra approach which leads to the investigation of the so-called Evans function.
    The numerical algorithm for evaluating the Evans function uses explicitly the matrix representation of the Hodge star operator and the numerical integrator that respects the Plücker imbedding of the Grassman manifold into the space of exterior forms.

  • Eusebius J. Doedel (Concordia Univ., Montreal): Continuation of Periodic Solutions in Conservative Systems with Application to the N-Body Problem
    02.10.2002, 14:15, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse
    Abstract: I will show how boundary value continuation software can be used to compute families of stable and unstable periodic solutions of conservative systems. A simple example will be used to illustrate the main idea. I will show how the computational approach can be used to follow the recently discovered figure-8 orbit of Montgomery, Chenciner, and Simo, as the mass of one of the bodies is varied. The numerical results show, among other things, that there exists a continuous path from the figure-8 orbit to periodic solutions of the restricted three body problem.
    Various aspects of this work are done in cooperation with Andre Vanderbauwhede (Gent), Don Dichmann (Aerospace Corporation), Jorge Galan (Sevilla), and Herb Keller and Randy Paffenroth (Caltech).

  • Björn Sandstede (Ohio State Univ., Columbus): Spectral properties of spiral waves
    11.07.2002, 12:30, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse

  • Andreas Keese (Braunschweig): Numerische Lösung von Systemen mit stochastischem Operator
    20.06.2002, 12:30, V2-216, Seminar der Forschergruppe Spektrale Analysis, asymptotische Verteilungen und stochastische Prozesse

  • Werner Vogt (TU Ilmenau): Zur numerischen Approximation invarianter Tori und quasi-periodischer Lösungen dynamischer Systeme
    07.06.2002, 14:15, V5-148, Oberseminar Numerik

  • Kurt Lust (Leuven): Accurate computation of Floquet multipliers in multiple shooting and Gauss-Legendre codes
    13.02.2002, 14:15, V5-148, Oberseminar Numerik

  • Arno F. Münster (Würzburg): Strukturbildung in chemischen Reaktionen mit Ionen
    22.11.2001, 10:15, W9-109, Seminar GK Strukturbildungsprozesse

  • Qin Mengzhao (Peking): Multisymplectic methods for infinite-dimensional Hamiltonian systems
    16.11.2001, 14:15, U5-133, Oberseminar Numerik

  • Alexander Lust: Numerische Berechnung von Liapunow-Exponenten
    07.11.2001, 14:15, V5-148, Oberseminar Numerik

  • Thorsten Hüls: Heterokline Orbits zwischen nichthyperbolischen Fixpunkten
    24.10.2001, 14:15, V5-148, Oberseminar Numerik

  • Sergey Pilyugin (St. Petersburg): New results on shadowing
    05.07.2001, 12:30, V2-205, Oberseminar Numerik