Numerische Spektralanalyse
unendlich-dimensionaler Transferoperatoren
07-025 Wolf-Jürgen Beyn, Thorsten Hüls, Malte Samtenschnieder.
On r-periodic orbits of k-periodic maps
In this paper, we analyze r-periodic orbits of k-periodic difference
equations, i.e.
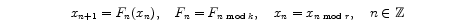
and their stability. This notion was introduced in [7]. We discuss
that, depending on the values of r and k, such orbits generically only
occur in finite dimensional systems that depend on sufficiently many
parameters, i.e. they have a large codimension in the sense of
bifurcation theory. As an example, we consider the periodically forced
Beverton-Holt model, for which explicit formulas for the globally
attracting periodic orbit, having the minimal period k = r, can be
derived. When r factors k the Beverton-Holt model with two
time-variant parameters is an example that can be studied explicitly
and that exhibits globally attracting r-periodic orbits. For
arbitrarily chosen periods r and k, we develop an algorithm for the
numerical approximation of an r-periodic orbit and of the associated
parameter set, for which this orbit exists. The algorithm is applied
to the generalized Beverton-Holt and the two-dimensional stiletto model.