Numerische Analyse äquivarianter
Evolutionsgleichungen
08-043 Jens Rottmann-Matthes.
Spectral Analysis of Coupled Hyperbolic-Parabolic Systems on Finite and
Infinite Intervals
In many applied problems in biology,
physics or chemistry traveling waves arise as solutions of systems of
partial differential equations of the form
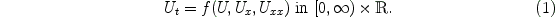
A traveling wave has the special property that it is constant if one
looks at it in a comoving frame. More precisely this means if U is a
traveling wave solution of (1) with speed c, the function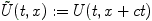 
is a steady state of the transformed PDE
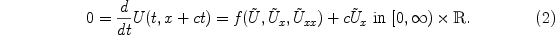
For the stability analysis of traveling waves it is important to know
where the point spectrum of the linearized right hand side of (2)
lies. We will show how this can be approximated by computing the
spectrum of boundary value problems.
