
 |
 |

|
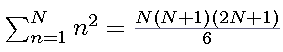
Für N = 24 erhalten wir:
Frage: Ist es möglich, die Quadrate mit Seitenlängen 1,2,3,...,24
ohne Überlappungen in ein Quadrat mit Seitenlänge 70 zu legen?
Nein.
Immerhin schafft man folgendes: Man kann 23 dieser Quadrate ohne Überlappungen in ein Quadrat mit Seitenlänge 70 legen! Und zwar zum Beispiel alle bis auf das Quadrat mit Seitenlänge n = 7.
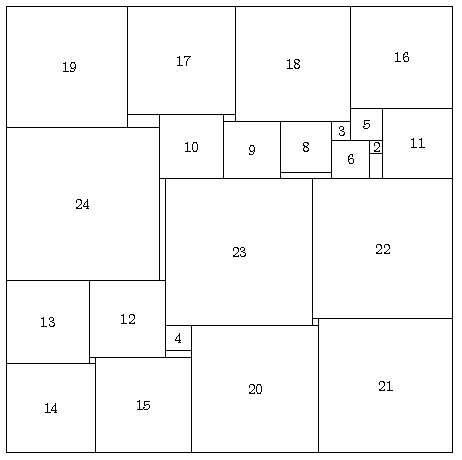
(Nicht beschriftet ist das 1x1-Quadrat). Es bleiben hier also Lücken; insgesamt ein Flächeninhalt von 72 = 49 Einheiten.
Ob n=7 die kleinste derartige Zahl ist, scheint unbekannt zu sein!
Allgemeinere Frage: Gegeben seien m paarweise verschiedene Quadrate. Wann
lassen sie sich zu einem Quadrat (oder zumindest einem Rechteck) zusammenfügen?
Antwort: Um ein Rechteck zu erhalten, muss m ≥ 9 gelten, um ein
Quadrat zu erhalten sogar m ≥ 21.
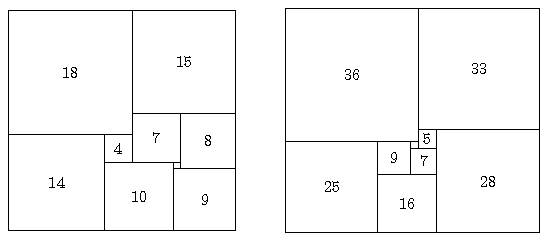
Nicht bezeichnet ist jeweils das kleinste Quadrat: links ein 1x1-Quadrat, rechts ein 2x2-Quadrat. Und zwar erhält man links ein Rechteck mit Seitenlängen 32 und 33, rechts eines mit Seitenlängen 61 und 69.
Ein derartiges Packproblem wird zum Beispiel im neuen Mathematik-Museum Mathematik zum Anfassen in Giessen gezeigt.
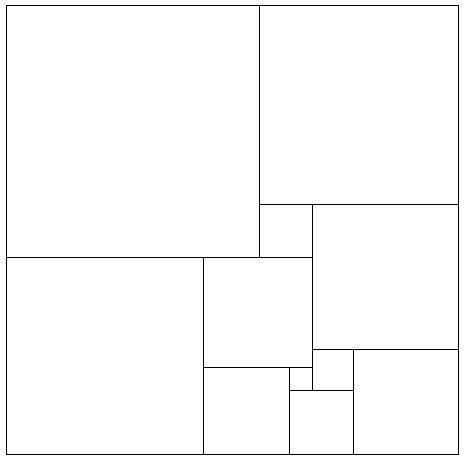
Kennt man nur die Zerlegung, also etwa die des linken Beispiels:
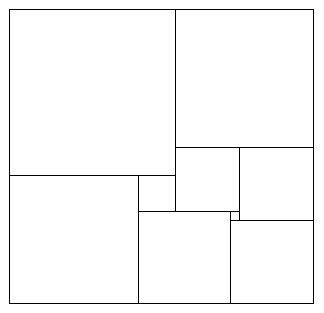
so lassen sich die möglichen Quadratgrößen einfach berechnen.
Zum Beispiel als Lösungen eines homogenen Gleichungssystems:
| Gleichungssystem: | |||||||||||||
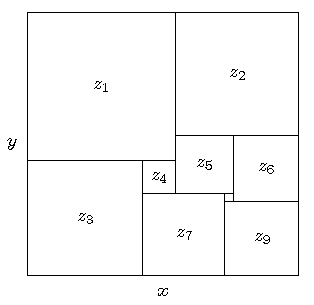
| +z1 | +z2 | - x | = 0 | |||||||||
| +z1 | +z5 | +z6 | - x | = 0 | |||||||||
| +z3 | +z4 | +z5 | +z6 | - x | = 0 | ||||||||
| +z3 | +z6 | +z7 | +z8 | - x | = 0 | ||||||||
| +z3 | +z7 | +z9 | - x | = 0 | |||||||||
| +z1 | +z3 | - y | = 0 | ||||||||||
| +z1 | +z4 | +z7 | - y | = 0 | |||||||||
| +z2 | +z5 | +z7 | - y | = 0 | |||||||||
| +z2 | +z5 | +z8 | +z9 | - y | = 0 | ||||||||
| +z2 | +z6 | +z9 | - y | = 0 | |||||||||
| Lösungen:
Alle Vielfachen von
(18,15,14,4,7,8,10,1,9,33,32) | |||||||||||||
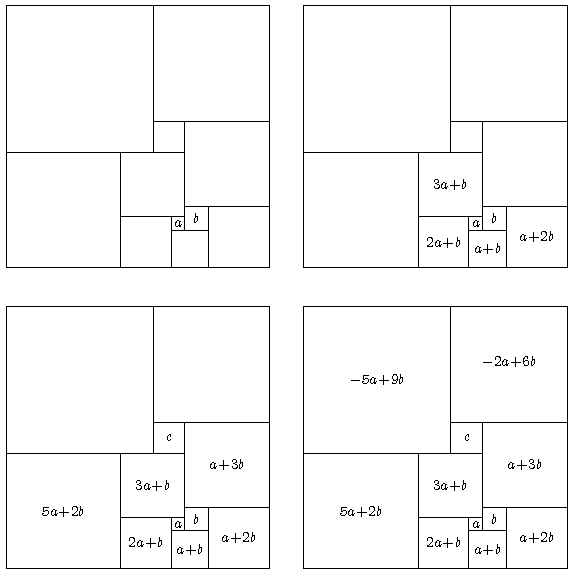
Dabei berechnet sich c als Differenz c = (2a+5b)-(5a+2b) = -3a+3b.
Die Breite des Rechtecks ist oben -7a+15b, unten 9a+6b. Daraus folgt: 9b = 16a.
Wählen wir a=9, b=16, so erhalten wir eine Lösung (und zwar die kleinstmögliche ganzzahlige Lösung):
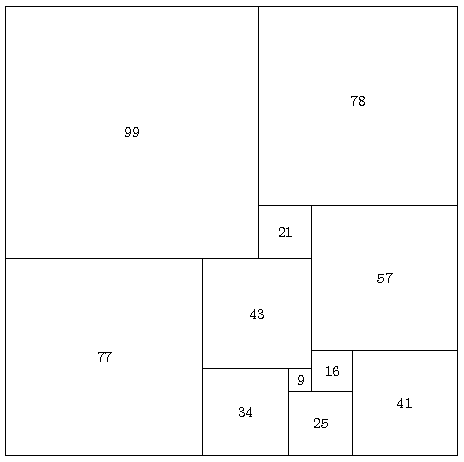
Es handelt sich also um ein Rechteck der Größe 176 x 177.
Bisher erhielten wir Rechtecke, keine Quadrate. Wie gesagt, wir brauchen mindestens 21 Quadrate, um ein Quadrat zu legen:
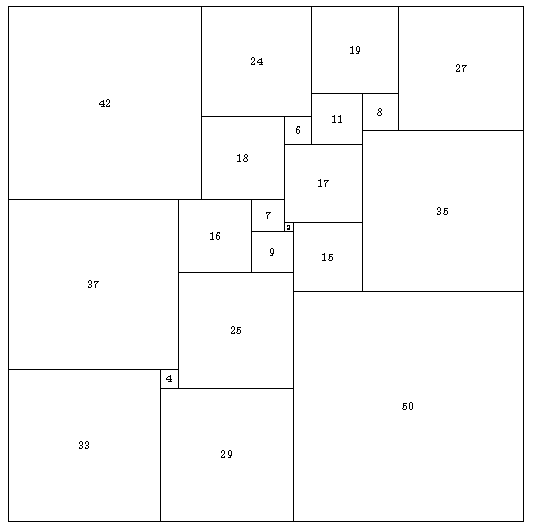
Nicht nur der ICM in Beijing, sondern auch der vorangehende ICM in Berlin im Jahr 1998 hat die Bedeutung von Quadraten für die Mathematik betont. Hier ist die Sondermarke, die anlässlich des ICM herausgegeben wurde:
Es handelt sich gerade um die Übderdeckung des Rechtecks 176x177 durch 11 Quadrate!