Algebras of odd degree with involution, trace forms and dihedral extensions

by D. E. Haile, M.-A. Knus, M. Rost, and J.-P. Tignol (47 pages)

Israel J. Math. 96 B, 299-340 (1996) - Amitsur Volume

MR 1433693, Zbl 871.16017.

A 3-fold Pfister form is associated to every involution of the second kind on a central simple algebra of degree 3. This quadratic form is associated to the restriction of the reduced trace quadratic form to the space of symmetric elements; it is shown to classify involutions up to conjugation. Subfields with dihedral Galois group in central simple algebras of arbitrary odd degree with involution of the second kind are investigated. A complete set of cohomological invariants for algebras of degree 3 with involution of the second kind is given.

The beautiful identity

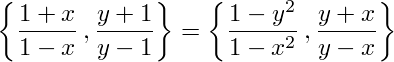
{(1+x)/(1-x),(y+1)/(y-1)}={(1-y^2)/(1-x^2),(y+x)/(y-x)}

in K2 of a field is used for computations with symbols in Galois cohomology.

Full text (may differ slightly from the original article): [tex] [dvi] [dvi.gz] [ps] [ps.gz] [pdf] [pdf.gz]

Go to: Publications and Preprints · Markus Rost's Web Page