Go to: Associahedron and associator identities · Publications and Preprints · Markus Rost's Web Page
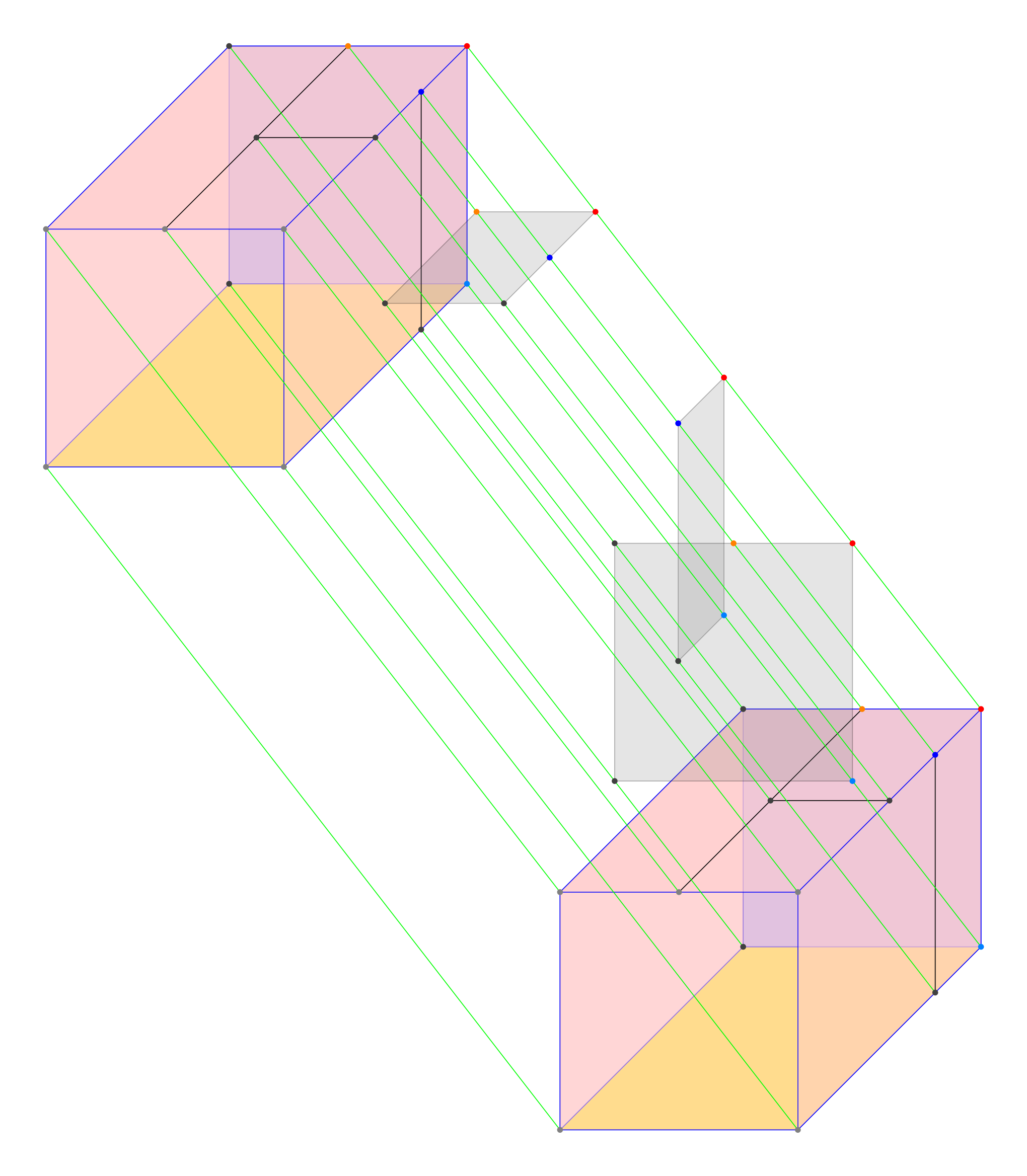
The diagrams show the 1-skeleton with all 42 vertices and 84 edges.
The 28 edges parallel to the 4th basis vector are drawn in green. The others form two opposite embeddings •(...), (...)• of the 3-dimensional associahedron (each with 21 edges) and three 2-cells (two pentagons and one quadrilateral). These are all the cells parallel to the 3-dimensional associahedra.
The arrows represent a process •(••) → (••)•. The terminal vertex is ((((01)2)3)4)5 (the red point on the bottom cuboid).
In the second and third diagram the black (as opposed to blue) arrow heads depict for each vertex the "canonical directed path" (Mac Lane 1963 MR 170925 p. 34) to the terminal vertex.
The labels in the fourth diagram are the Tamari indices as in the diagrams up to dimension 3 in Tamari's diagram.
The images have a high resolution (2188x2085). Go full screen to marvel at them. To access them directly click on the images or the links above.
Go to: Associahedron and associator identities · Publications and Preprints · Markus Rost's Web Page