Prelude

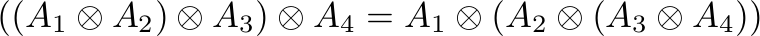
Notes on the associator

by Markus Rost (Notes, April 2024/August 2025, 38 pages)

• April 2024: We discuss the 5-term relation for associators, its relation with the associahedron and ask questions.

  

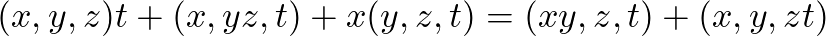
• May 2024: Added references to alternative algebras.
• December 2024: Section 6 has an essentially complete discussion of the associahedral chain complex and its acyclicity. Section 7 has beautiful diagrams!
• August 2025: There are no essential changes since December 2024. Only some corrections, a few further comments and an addition of diagrams.

Full text (August 21, 2025): [pdf]

The associahedral chain complex and the cubical associahedron

by Markus Rost (Notes, August/October 2025, 45 pages)

• The first part is a detailed introduction to multi-magmas (partially parenthesized words).
• The associahedral chain complex is constructed algebraically and its acyclicity is proven. All details are given.
  (It seems that this part is new. Please tell me if you think otherwise.)
• The cubical associahedron is constructed, also with all details.
  (This part is perhaps new as well.)
• The sign game relating the definition of A(∞)-algebras is detailed.
• Related material on coderivations is developed.
• The associahedral automorphism group is discussed.
• Possible expansions are indicated.

Full text (October 25, 2025): [pdf]

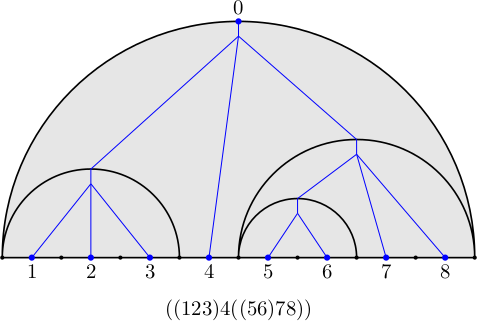
The picture illustrates the well known 3-fold dictionary:

• Partially parenthesized words.
• Rooted plane trees.
• Partial triangulations of polygons with selected edge. Here the edges of the "polygon" are put on a line except for the selected edge which is drawn as the outer half circle. The inner half circles are non-crossing "diagonals" (the diameter of each half circle is at least 2).

This way of presentation makes it easy to describe products: juxtapose several diagrams on the base line, draw a new outer half circle, add its tree.

Associahedron drawings

• Tamari's diagram
• Associahedra and polygon triangulations
• Cubical drawings from other sources

Cubical associahedron drawings

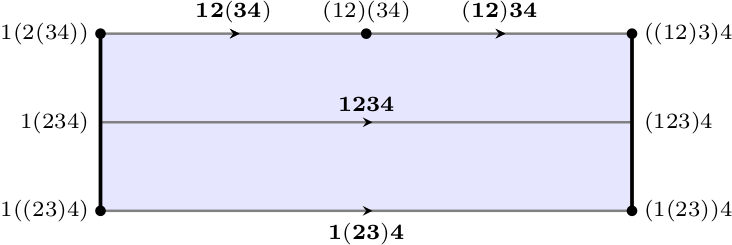
The 2-dimensional associahedron

The pentagon as rectangle with an edge subdivided:

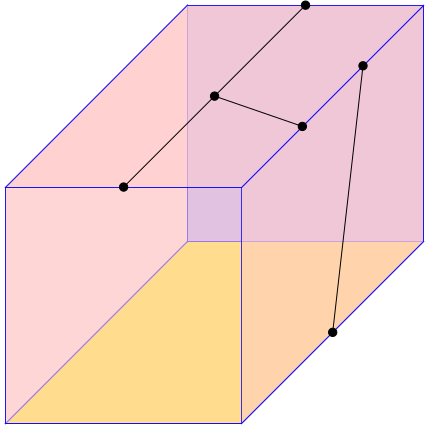
The 3-dimensional associahedron

Main page: The 3-dimensional associahedron unfolded

As cuboid with two faces subdivided:

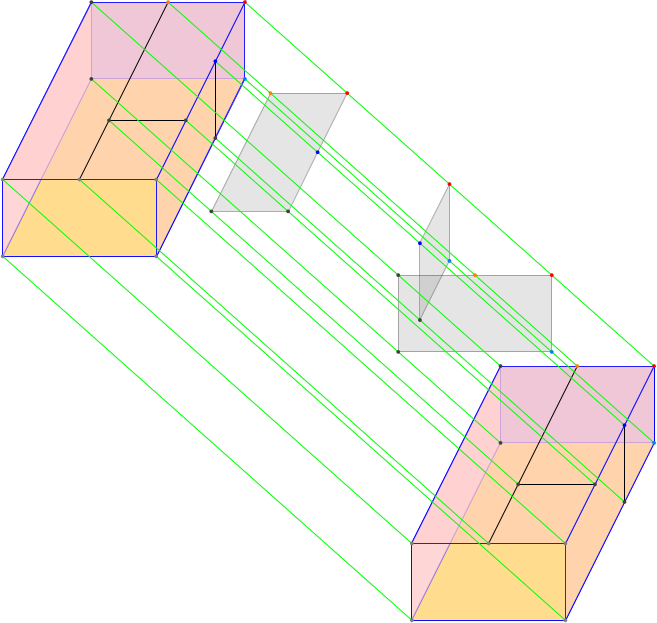
The 4-dimensional associahedron

Main page: The 4-dimensional cubical associahedron

The first image shows the 1-skeleton with all 42 points and 84 edges. Further the two basic 3-dimensional subassociahedra •(...), (...)• (the shoebox cuboids) and the cells parallel to them.

[high resolution image]

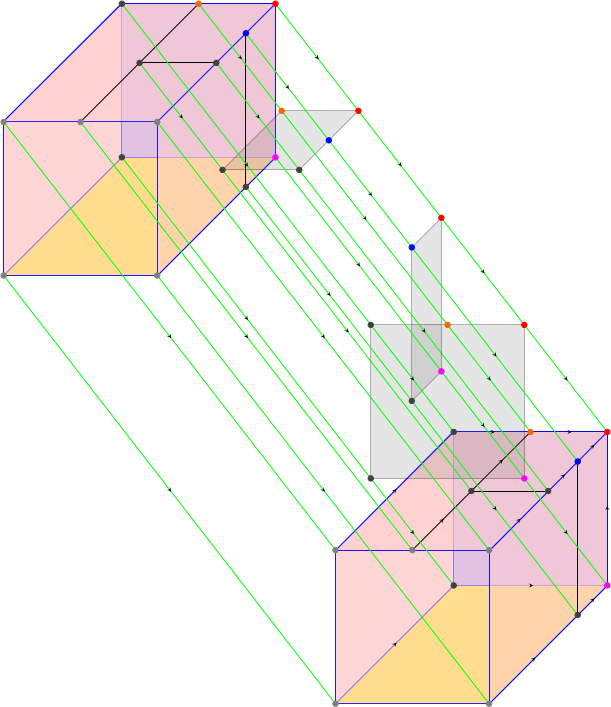
The next image includes orientations of the edges. The black (as opposed to blue) arrows depict for each point the "canonical directed path" (Mac Lane 1963 MR 170925 p. 34) to the base point (the red one on the bottom cuboid).

[high resolution image]

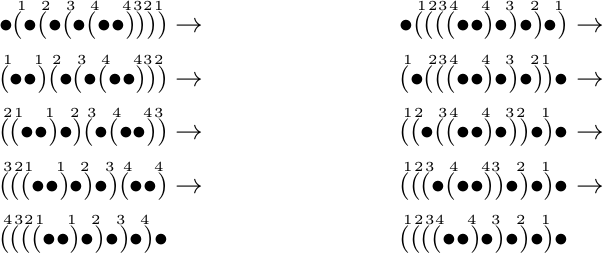
Here are labels for

• the path with 4 directions (starting in the gray left bottom corner of the upper cuboid)
• the maximal path with no direction change (the rightmost green line with the 5 red points)

The parenthesis pairs are enumerated for identification along the path. See also cube-4-84-parens-large.png.

[high resolution image]

[black and white]

Notes on associator identities

by Markus Rost (Notes, May 2024, 10 pages)

The text contains notes on some (well-known) identities in non-associative algebras.

Among other things, we establish the 5-term relation for associators and this identity in alternative algebras:

Full text (June 18, 2024): [pdf]

Notes on free alternative algebras

by Markus Rost (Notes, June 2024, 12 pages)

We compute the free alternative algebra up to degree 4.

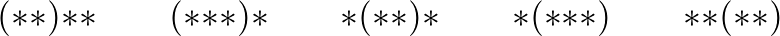
Full text (June 22, 2024): [pdf]

TeX sources for the displayed formulas: A1A2A3A4.tex · assoc1.tex · assoc4.tex · assoc5.tex

TeX sources for the drawings and the parens: halfcircles.tex · diagram2.tex · cube-3.tex · cube-4-84.tex · cube-4-labels.tex

Go to: Publications and Preprints · Markus Rost's Web Page