Semiorthogonal decompositions for representations of algebraic groups
Monday 01 September to Wednesday 03 September 2025
Semiorthogonal decompositions are a well-established tool for the study of derived categories in algebraic geometry and in the representation theory of Artin algebras. The goal of this meeting is to discuss semiorthogonal decompositions that arise in the representation theory of algebraic groups, going over the main proofs of the recent work arXiv:2407.13653 of Samokhin and van der Kallen, and exploring emerging connections to geometric representation theory.
After the end of the workshop, participants will have the possibility for informal discussions as well as presentations of research talks on Thursday, September 4.
Location: Bielefeld University
Organisers: Wassilij Gnedin, Henning Krause, Eike Lau, Charles Vial
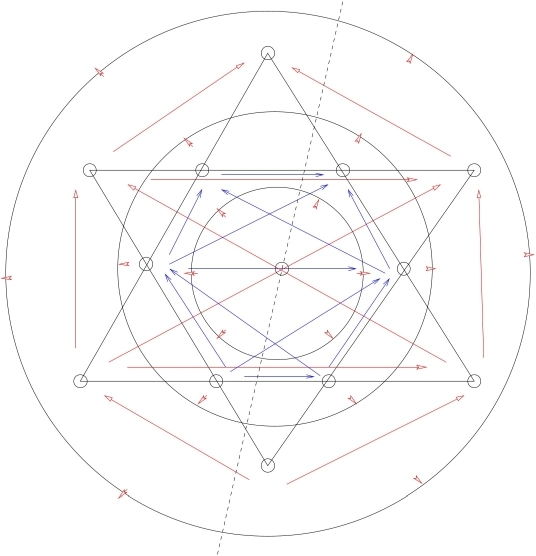
of the adjoint representation of type G2
Image credit: Wilberd van der Kallen, 2025
Invited Speakers
- Alexey Ananyevskiy (Munich)
- Stefan Dawydiak (Bonn)
- Juan Omar Gomez (Bielefeld)
- Andreas Krug (Hannover)
- Dmitry Kubrak (Paris)
- Marco Rampazzo (Antwerp)
- Kostiantyn Tolmachov (Hamburg)
- Antoine Touzé (Lille)
- Wilberd van der Kallen (Utrecht)
A detailed programme can be found below.
If you would like to attend the conference, please register using the webform.
In the week before the workshop, the conference "The Legacy of Peter Gabriel" will be held at Bielefeld University.
Funding
This workshop is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) via the TRR 358 "Integral Structures in Geometry and Representation Theory".
Picture
Contact
If you have any questions about the conference, please contact the organisers at birep.
