List of Publications

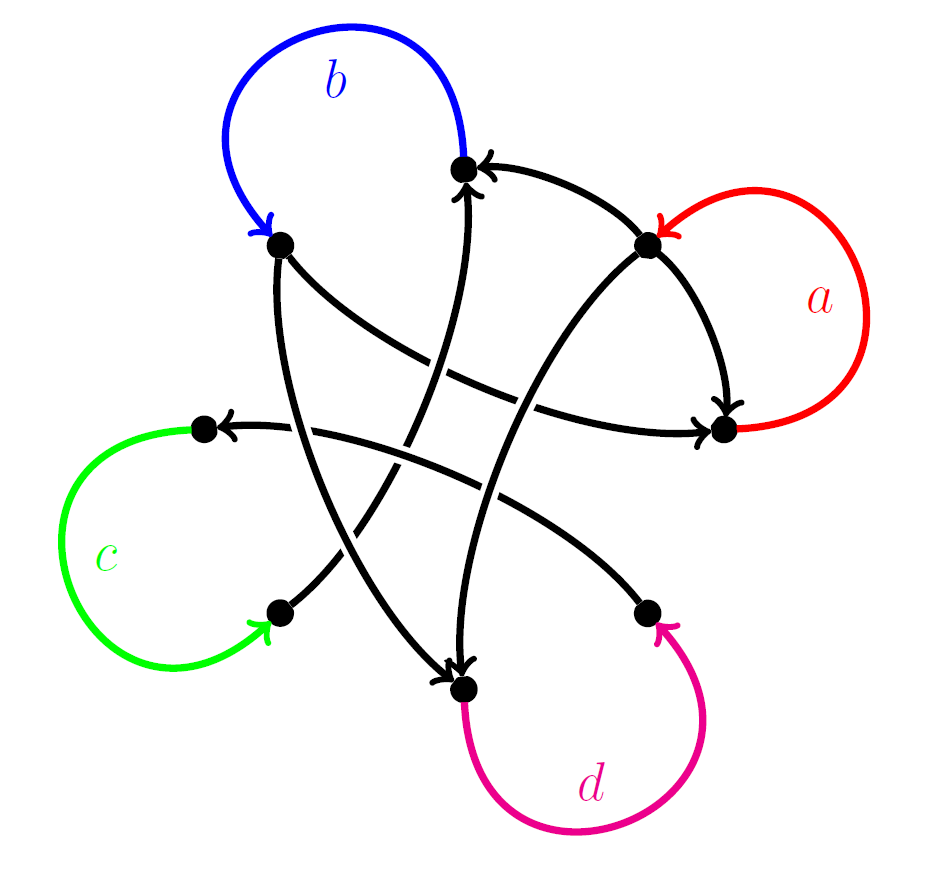
Zeckendorf representations and mixing properties of sequences
by N. Manibo, E. D. P. Miro, D. Rust, G. S. Tadeo
Tsukuba Journal of Mathematics (2020) in print
arXiv, PDF (226k)

A modification of Wythoff's Nim
by R. Fokkink, D. Rust
Preprint (2019)
arXiv, PDF (513k)

Periodic points in random substitution subshifts
by D. Rust
Preprint (2018)
arXiv, PDF (376k)

Shifts of finite type and random substitutions
by P. Gohlke, D. Rust, T. Spindeler
Discrete and Continuous Dynamical Systems 39(9), 5085 - 5103 (2019)
arXiv, DOI

Dynamical systems arising from random substitutions
by D. Rust, T. Spindeler
Indagationes Mathematicae 29(4), 1131 - 1155 (2018)
arXiv, DOI

Beyond primitivity for one-dimensional substitution subshifts and tiling spaces
by G. R. Maloney, D. Rust
Ergodic Theory and Dynamical Systems 38(3), 1086 - 1117 (2018)
arXiv, DOI

Computations for Symbolic Substitutions
by S. Balchin, D. Rust
Journal of Integer Sequences 20, Article 17.4.1 (2017)
arXiv, DOI (open access online)

An uncountable set of tiling spaces with distinct cohomology
by D. Rust
Topology and its Applications 205, 58 - 81 (2016)
arXiv, DOI

PhD Thesis

Cohomology of Tiling Spaces: Beyond Primitive Substitutions
by D. Rust
PhD Thesis, University of Leicester, Leicester, 2016.
Leicester Research Archive, PDF (828k)

Slides

Random Substitutions, Mixing and Rauzy Fractals (expert audience) (9.9M)

Random Substitutions, Mixing and Rauzy Fractals (general audience) (11.7M)

Random Substitutions (183k)

Ordered cohomology and co-dimension one cut-and-project sets (1.4M)

Dynamics of stochastic substitution subshifts (173k)

The strange topology of aperiodic tilings and their cohomology: Grout (1.8M)

Programs

Grout

Authors: S. Balchin, D. Rust
Grout is a free user-friendly program for Windows and Mac which can calculate various topological and combinatorial properties of primitive symbolic substitutions.
For an explanation of the computations that Grout performs, we have provided documentation on the arXiv.
You can download Grout from the homepage of Scott Balchin on the University of Leicester website or from Github.

Research Interests

My research is focused on the topology and dynamics of spaces associated to aperiodic tilings and quasicrystals. Specific topics include:

The representation of tiling spaces as inverse limits of branched manifolds and their Čech cohomology
The translational (and other) dynamical systems of tilings and bi-infinite sequences - especially those arising from substitutions and more general mixed and random families of substitutions, and also those arising from cut and project methods
Applications of tiling theory to other areas of mathematics - specifically the study of dimension groups and Diophantine approximation

I also have interests in topological dynamics, as well as algebraic topology as a whole. I have a particular fondness for the applications of algebraic topology to the study of braid groups on manifolds, TQFTs and knot theory.

The Barge-Diamond complex of a substitution on four letters