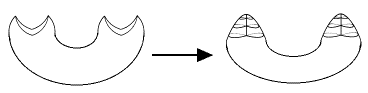4. Konstruktion kompakter Flächen
Polygon-Modelle
Beispiele.
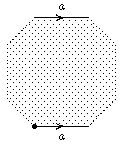
Wir beginnen mit dem Quadrat Q = {(x,y)| 0 ≤ x ≤ 1 und 0 ≤ y ≤ 1}
und identifizieren die linke Kante mit der
rechten Kante: es gibt zwei wesentlich verschiedene Möglichkeiten:
- (0,t) ~ (1,t) für alle t mit 0 ≤ t ≤ 1.
Wir erhalten einen Schlauch (Zylinder, Henkel).
- (0,t) ~ (1,1-t) 0 für alle t mit ≤ x ≤ 1.
Wir erhalten ein Möbiusband (Man nennt dies
auch eine "Kreuzhaube", wir werden später noch genauer darauf
eingehen!)
Allgemeiner Fall.
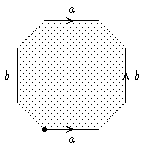
Sei nun M ein regelmäßiges n-Eck -
oder der Einheitskreis, auf dem die n-ten Einheitswurzeln
markiert sind. Wenn wir von Kanten des n-Ecks sprechen, so
sind diese bei Betrachtung des Einheitskreises durch die
Kreisbögen zwischen zwei benachbarten Einheitswurzeln zu
ersetzen!
Das Kreismodell hat den Vorteil, dass wir hier auch den Fall
n=2 betrachten können, der uns auch interessiert!
Greifen wir ein Kantenpaar heraus, so können wir eine der beiden
Identifizierungen vornehmen. Ist n gerade und verwenden wir hierbei
jede Kante genau zweimal, so erhalten wir eine kompakte geschlossene
Fläche F. Dies soll bedeuten:
- F ist Hausdorffsch.
- Jeder Punkt hat eine Umgebung, die zu R2
homöomorph ist.
- F besitzt eine abzählbare Umgebungsbasis.
- F ist kompakt.
Unter einem Polygon-Modell einer geschlossenen Fläche
verstehen wie ein regelmäßiges 2m-Eck mit einer
Identifikationsvorschrift
für Kantenpaare: die Menge der Kanten ist in m Kantenpaare eingeteilt;
für jedes derartige Kantenpaar ist angegeben, in welcher der beiden
möglichen Weise diese Kanten zu identifizieren sind.
|
Lemma.
Zu jeder endlich-triangulierbaren zusammenhängenden
geschlossenen Fläche gibt es ein Polygonmodell.
|
Beweis: Betrachte endliche Zerlegungen der Fläche,
so dass die Komponenten Polygone sind
(oder wenigstens topologisch äquivalent zu Polygonen). Zum Beispiel
wird ja vorausgesetzt, dass es eine Zerlegung in endlich viele 2-Simplizes
gibt. Nimm eine Zerlegung mit kleinstmöglicher
Zahl von Komponenten. Ist diese Zahl größer als 1,
so kann man zwei Komponenten zusammenkleben und erhält einen Widerspruch.
Notation für Polygon-Modelle
Um die Identifikationsvorschrift zu beschreiben, verwenden wir "Wörter"
wie folgt: Ausgehend von einer festen Ecke durchlaufen wir die Kanten des
Rands entgegen dem Uhrzeigersinn. Wir bezeichnen die ersten
Kanten nacheinander mit
a1, a2,... und notieren eine Art Produkt
a1a2...at (eben ein "Wort" mit Buchstaben
a1,...).
Kommen wir allerdings zu einer Kante, die mit einer schon betrachteten Kante
zu verheften ist, etwa mit ai,
so schreiben wir als nächsten Buchstaben ai, falls die
Identifizierung den Durchlaufsinn nicht ändert, oder
ai-1, falls sie ihn ändert.
Frage: Welche Wörter liefern homöomorphe Flächen?
Welche nicht?
Satz 4 (Klassifikationssatz, Aussage 1).
Jede endlich-triangulierbare zusammenhängende geschlossene Fläche
ist topologisch äquivalent zu einer der folgenden Flächen:
- F0 - dies ist die Flächen-Realisierung des Worts aa-1.
- Fg - dies ist die Flächen-Realisierung des Worts
a1b1a1-1b1-1
...
agbgag-1bg-1
mit g > 0.
- Ng - dies ist die Flächen-Realisierung des Worts
a1a1a2a2....agag mit g > 0.
|
Die zweite Aussage von Satz 4 wird besagen, dass Flächen mit verschiedener Normalform nicht topologisch
äquivalent sind. Dies wird erst später bewiesen.
Reduktionen
- Reduktion I: Elimination von aa-1 (falls die Länge
des Gesamtworts echt größer als 2 ist)
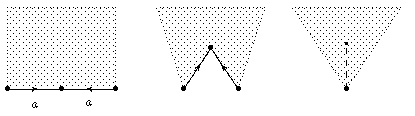
- Reduktion II: Eckpunkt-Reduktion. Da Kanten unter der Quotientenabbildung π identifiziert werden,
werden auch Eckpunkte identifiziert.
Die Eckpunkt-Reduktion wird so lange durchgeführt, bis
es nur eine Äquivalenzklasse von Eckpunkten gibt.
(Gegebenenfalls müssen zwischendurch Reduktionen der Form I
durchgeführt werden.)
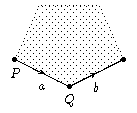
Bezeichne mit m(P)
die Kardinalität von π-1π(P). Wähle P mit
m(P) maximal, und zwar so, dass einer der Nachbarpunkte von P unter π
nicht mit P identifiziert wird. Sei dies Q, und die Kante zwischen ihnen sei
a.
Die nachfolgende Kante kann nicht a sein, denn a beginnt in P, die folgende
Kante beginnt in Q. Sie kann auch nicht a-1 sein, denn Paare
der Form aa-1 sind schon eliminiert. Also nennen wir sie b,
ihr Endpunkt sei R.
Durch einen Schnitt von P nach R und Zusammenkleben
entlang b erhalten wir ein neues Modell:
(Bilderklärung, von links nach rechts:
Links das Ausgangsmodell, der Rand ist
punktiert, soweit nicht die für die Betrachtung wichtigen Kanten
hervorgehoben sind.
In der Mitte ist der Schnitt eingezeichnet (grob gestrichelt).
Rechts ist die neue Konfiguration angegeben, die dadurch entsteht,
dass nach dem Schneiden neu verklebt wird.
Die übereinander stehenden Skizzen thematisieren
die beiden möglichen Fälle für die zweite b-Kante.)
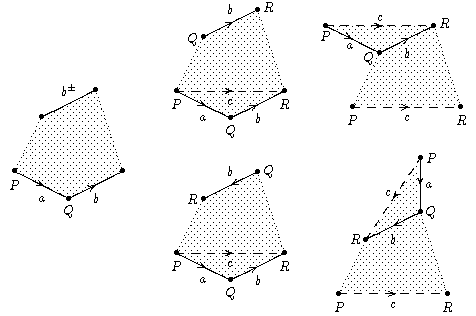
Und im neuen Modell hat sich m(P) um 1 erhöht!
Im oberen Fall wird also abCb-1D durch cCc-1aD ersetzt.
Im unteren Fall wird abCbD durch cCa-1cD ersetzt.
- Reduktion III: Kreuzhauben-Normierung
Ersetze a...a... durch aa...
Genauer: Ersetze aCaD durch
bbC-1D (C und D stehen für Wörter).
- Reduktion IV: Henkel-Normierung
Wir betrachten nun ein Wort w der Form ...a...a-1...
Wir können annehmen, dass w mit a anfängt, etwa w =
aBa-1C, wobei B und C Wörter sind.
Behauptung: Es gibt mindestens eine Kante, die sowohl in B als
auch in C vorkommt. Denn sonst würde ein Eckpunkt rechts (also im
B-Teil)
auf keinen Fall mit einem Eckpunkt links (im C-Teil)
identifiziert: es gäbe also mindestens zwei
Äquivalenzklassen von Eckpunkten im Gegensatz zur zweiten Reduktion!
Also sieht unser Polygon-Modell so aus:
 ,
,
wobei wir uns noch überlegen müssen, wie die zweite b-Kante
orientiert ist. Sie muss aber die Form b-1 haben, denn
wir haben ja alle Kreuzhauben normiert: kommt b zweimal in gleicher
Orientierung vor, so direkt nacheinander.
Zwei Schritte sind notwendig. Im ersten Schritt
ersetze das Wort a...b...a-1...b-1... durch
ein Wort der Form aba-1...b-1....
(Genauer: aAbBa-1Cb-1D kann ersetzt werden durch
aca-1CBc-1AD):
Für den zweiten Schritt können wir annehmen,
dass wir ein Wort der Form
aba-1...b-1... vor uns haben. Im zweiten Schritt
ersetze aba-1...b-1... durch ein Wort der
Form aba-1b-1...
(Genauer: Ersetze aba-1Ab-1B durch
cbc-1b-1BA):
- Reduktion V: Henkel-Elimination (falls es Kreuzhauben gibt)
Wir betrachten ein Wort w, das sowohl Kreuzhauben als auch Henkel besitzt.
Wir können demnach annehmen, dass es mit
aba-1b-1cc... beginnt. Wir ersetzen es
durch abdbad...
Anschließend müssen diese Kreuzhauben wieder
normiert werden:
- Reduktion II ersetzt abdbadE durch
a'a'b-1d-1b-1dE, also nach Rotation
b-1d-1b-1dEa'a'.
- Eine zweite Anwendung der
Reduktion II ersetzt b'd-1b'dEa'a'
durch b'b'ddEa'a', also nach Rotation haben wir a'a'b'b'ddE.
Merkregel:
Die Flächen zu
aba-1b-1ccE und aabbccE sind topologisch
äquivalent. (Dabei ist E ein beliebiges Wort.)
Mehr zu den Normalformen
Dass Flächen mit verschiedener Normalform nicht topologisch
äquivalent sind, kann hier noch nicht bewiesen werden - dazu
müssen wir geeignete Invarianten entwickeln ("Homotopiegruppen" oder
"Homologiegruppen", also algebraische Objekte; oder zumindest Zahlen:
"Betti-Zahlen", "Euler-Charakteristik", ...).
| g | Name | | | Euler-Charakteristik
|
|---|
| Fg | 0 | 2-Sphäre | orientierbar | | 2
|
| 1 | Torus | | 0
|
| 2 | Brezel | | -2
|
| .... | ... | | ...
|
| g | ... | | 2-2g
|
| .... | ... | | ...
|
| Ng | 1 | Projektive Ebene | nicht orientierbar | | 1
|
| 2 | Klein'sche Flasche | | 0
|
| ... | ... | | ...
|
| g | ... | | 2-g
|
| .... | ... | | ...
|
Das Anheften von Henkeln und Kreuzhauben
Hier soll nun noch ein wenig die Anschauung geschult werden: Wie stellt man sich
die Normalformen vor? Im R3 sind nicht alle Normalformen
realisierbar, höchstens mit Trick, nämlich mit
"Selbstdurchdringungen", die man sich wegdenken muss.
Wir betrachten ein Wort der Form
s1s1-1w1...stst-1wt,
wobei wi entweder die Form aibiai
-1bi-1 oder die Form cici hat.
Die zugehörige Fläche entsteht aus der 2-Sphäre auf folgende Weise:
- Schneide t Löcher in die 2-Sphäre
(mit disjunkten Rändern - deswegen haben wir die
eigentlich überflüssigen Buchstaben
s1s1-1 eingefügt)!
- Hefte Henkel an!
Ist wi von der Form aibiai
-1bi-1, so identifiziere den Rand des i-ten
Lochs mit dem Rand eines gelochten Torus.
- Hefte Kreuzhauben an!
Ist wi von der Form cici, so identifiziere den Rand des i-ten Lochs mit dem Rand eines Möbiusbands.
Und es gilt:
- Der Klassifikationssatz besagt: Jede kompakte geschlossene Fläche ensteht aus der 2-Sphäre
durch Anheftung von Henkeln und Kreuzhauben.
- (Reduktion V) Das Anheften einer Kreuzhaube und eines Henkels liefert
das Gleiche wie das Anheften dreier Kreuzhauben.
Also:
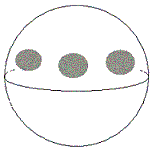
1. Löcher in die 2-Sphäre schneiden:
Hier eine 2-Sphäre mit drei Löchern:
2. Das Anheften eines Henkels:
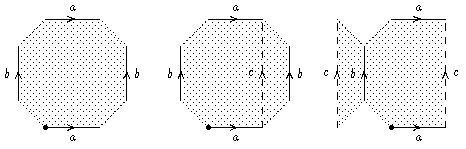
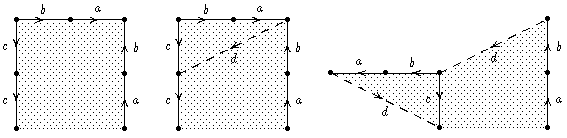
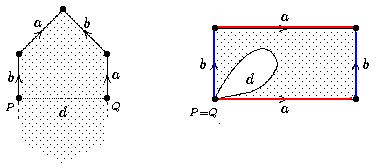
Wir betrachten also den Fall eines Teilworts der Form w =
aba-1b-1.
Wir schneiden vom Polygon das entsprechende Fünfeck ab
(linkes Bild, dabei ist d die Schnittkante); wichtig ist, dass man
sich merkt, dass die Punkte P und Q zu identifizieren sind.
Rechts das abgeschnittene Fünfeck, wobei die Identifizierung der
Punkte P und Q durchgeführt ist (die der a-Kanten und die der b-Kanten
jedoch nicht) - man sieht, dass
es sich nach Identifizierung der a-Kanten wie der b-Kanten
wirklich um einen Torus mit Loch handelt.
Hier der Torus mit Loch (das nach unten gezogen wurde):
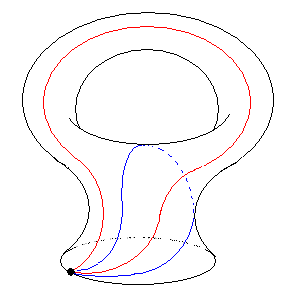
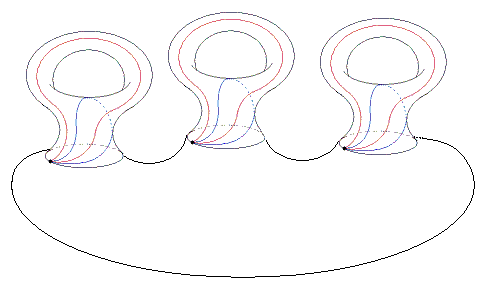
Als Beispiel eine 2-Sphäre mit drei angehefteten Henkeln:
Meist wird man das Anheften eines Henkels ein wenig anders beschreiben:
statt ein Loch auszuschneiden:

werden zwei Löcher
ausgeschnitten und durch einen Schlauch verbunden:

Es ist offensichtlich, dass die Ergebnisse (jeweils rechts)
topologisch äquivalent
sind!
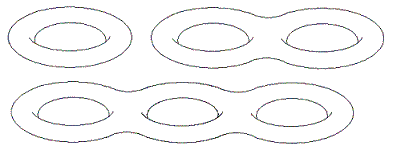
Für g=1,2,3 erhält man folgende Flächen Fg:
3. Das Anheften einer Kreuzhaube:
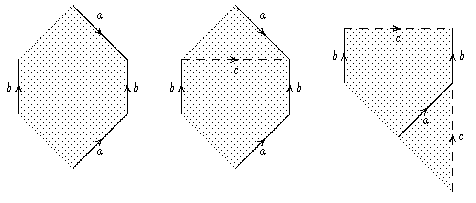
Wir betrachten also den Fall eines Teilworts der Form w = cc.
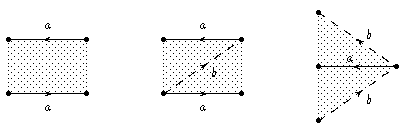
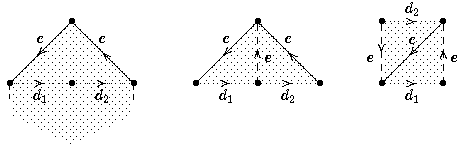
Wir schneiden vom Polygon das entsprechende Dreieck ab (linkes Bild) und unterteilen dabei die Basis in zwei Strecken d1 und d2.
Zerschneiden wir dieses Dreieck in der Mitte (mittleres Bild) durch eine
Kante e und verkleben wir die beiden c-Kanten (rechtes Bild), so
sehen wir ein Möbiusband mit Rand d1d2.
Merkregel. Jedes Teilwort der Form cc bedeutet gerade das Ersetzen
einer Kreisscheibe durch ein Möbiusband.
Zur Veranschaulichung empfiehlt es sich, an die bei jeder Einbettung in den
R3 auftretende Selbstdurchdringung zu denken. Zum Beispiel kann man diese berücksichtigen, indem man
c unterteilt, etwa c = ab schreibt, dann ist also cc = abab.
Schauen wir uns zum Beispiel ein Teilwort der Form eababe-1 an:
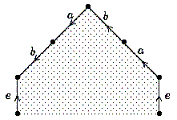
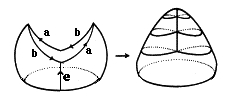
Wir sehen also: Das Ersetzen von ee-1
durch eababe-1 entspricht gerade dem Einsetzen eines M&oum;biusbands!
Möbiusbänder werden deshalb auch Kreuzhauben genannt!
Siehe: Kreuzhaube
Als Nächstes zeigen wir eine Veranschaulichung,
wie N2 ensteht:
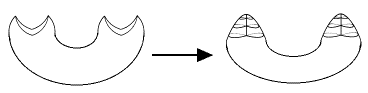
Für g=1,2,3 erhalten wir folgende Flächen Ng:
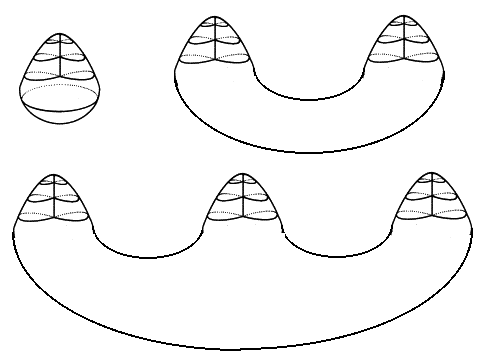





 ,
,