by Markus Rost (Notes, December 1996, 5 pages)
We associate to a pair of separable degree 3 extensions a 9-dimensional Jordan algebra of degree 3 and consider related del Pezzo surfaces.
Full text (version of July 29, 2003): [dvi] [dvi.gz] [pdf] [pdf.gz] [ps] [ps.gz]
by Markus Rost (Notes, March 2002, 3 pages)
In this note we describe a construction of the discriminant algebra of a flat cubic algebra over any commutative ring.
Full text (version of March 4, 2002): [dvi] [dvi.gz] [pdf] [pdf.gz] [ps] [ps.gz]
The construction is contained in the article "Discriminant Algebras of finite rank algebras and quadratic trace modules" by Ottmar Loos.
by Markus Rost (Notes, August 2003, 4 pages)
For a cubic element (or a triangle) we define its "basic line". It leads to the following normalization of cubic equations:
The method works in all characteristics for generic cubic elements. We describe for this 1-parameter family the discriminant extension and the corresponding variant of Cardano's formula:
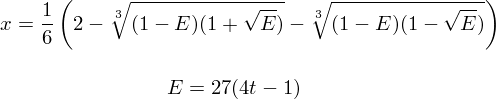
Full text (version of Mar 20, 2008): [dvi] [dvi.gz] [pdf] [ps] [ps.gz]
by Fabian Sander (diploma thesis, Universität Bielefeld, 2011, 45 pages)
The equation (due to Tate)
y2 + xy = x3 - (36x+1)/(j-1728)
yields over any ring (or scheme) an elliptic curve with J-invariant j (different from 1728). The general theory shows that every elliptic curve E (with j≠1728) is a form of the curve given by Tate's equation, twisted by an etale quadratic extension. If the latter is given by t2 - t + a = 0, the curve E is given by
(y2 - xy + ax2)/(1-4a) = x3 + (36x-1)/(j-1728)
This way one gets a normal from for any elliptic curve with J-invariant different from 1728 over any local ring. It depends only on the equation t2 - t + a = 0 for the associated Z/2Z-torsor.
The paper also contains a characterization of the origin x=y=0 of these normal forms. One can attach to an elliptic curve E (= a curve of genus 1 with point) a point C(E) in the ambient projective plane (this works over any scheme). This point is called the center of E (think of the center of circle). For the normal forms above, C(E) is just the origin x=y=0.
A toy model is here the normal form of a cubic extension, see Notes on cubic equations.
Full text: [pdf]
by Markus Rost (Notes, August 2018, 7 pages)
The text discusses briefly a certain presentation of the discriminant of cubic binary forms.
![[A presentation of the discriminant of cubic forms]](images/cubic-disc-det2.png)
Along the way I added remarks about Z/nZ-torsors for n = 2, 3.
Full text (version of Aug 17, 2018): [pdf]
See also
Further pages with related texts:
by Markus Rost (Notes, August 2003, 10 pages)
These notes evolved from a study of the fairly recent proof of Morley's theorem by Connes.
We briefly discuss the relation of Connes' point of view of affine transformations with triangles and quadrangles. Then we give a proof of Morley's theorem à la Connes. Finally we consider a purely group theoretic lemma which implies Connes' lemma on affine transformations.
Full text (version of August 26, 2003): [dvi] [dvi.gz] [pdf] [pdf.gz] [ps] [ps.gz]
Some sources for Morley's theorem:
by Markus Rost (Notes, February/April/May/August 2004, 21 pages)
Examples of triangle functions are given by the orthocenter, the circumcenter, the incenter, the excenters, the pedal points, the nine-point center, etc. Each of these functions has a "holomorphic extension" which is a complex function in four variables: the triangle points and the orthocenter.
For instance, for a triangle xyz with orthocenter t, the intersection of the lines xy and zt (a "pedal point" of xyz) is given by:
Full text (version of August 6, 2004): [dvi] [dvi.gz] [pdf] [pdf.gz] [ps] [ps.gz]
by Markus Rost (Notes, March 2004, 6 pages)
This text grew out of an attempt to understand the derived triangle construction. We consider the variety of (algebraic) angles of an Euclidean quadrangle and an action of S6 on it. (More details can be found below in the diploma thesis by S. Glied.) This action is induced from an action on a 5-dimensional torus.
Full text (version of January 18, 2007): [dvi] [dvi.gz] [pdf] [ps] [ps.gz]
by Svenja Glied (diploma thesis, Universität Bielefeld, 2007, 28 pages)
The major result of the thesis is the presentation of an S_6-symmetry of the set of similarity classes of (nondegenerate) Euclidean quadrangles. It is generated by the obvious S_4-symmetry (permutation of the points) and the so-called pedal triangle construction.
Furthermore, Lemma 1.18 describes the relations between the angles of a quadrangle. These are given by the obvious relations stemming from subtriangles (sum of angles = pi) but there is also a non-linear relation.
by Markus Rost (Notes, August 2004, 12 pages)
For n+2 points in affine n-space in general position there is a canonical metric (unique up to a similarity factor) such that complementary faces of the (n+2)-gon are orthogonal.
Full text (version of August 25, 2004): [dvi] [dvi.gz] [pdf] [pdf.gz] [ps] [ps.gz]