1. Definitionen, Beispiele

Grunddefinition

• Topologischer Raum: 
  Ein Paar (X,T), dabei ist X eine Menge, T eine Menge von Teilmengen von X mit folgenden Eigenschaften: 
  • Die leere Menge {} und X selbst gehören zu T.
  • T ist abgeschlossen unter endlichen Durchschnitten.
  • T ist abgeschlossen unter beliebigen Vereinigungen.
  Man nennt T eine Topologie auf X, die Mengen in T nennt man offene Mengen; statt (X,T) schreibt man meist einfach X.
• Stetige Abbildung: 
  Sind (X,T) und (X',T') topologische Räume und f: X → X' eine Abbildung, so nennt man f stetig, falls Urbilder offener Mengen offen sind.

  ---

  Homöomorphismus:  Eine stetige Abbildung f, die bijektiv ist und deren Umkehrabbildung ebenfalls stetig ist.
  Topologische Äquivalenz:  Zwei topologische Räume (X,T), (X',T') heißen topologisch äquivalent, falls es einen Homöomorphismus (X,T) → (X',T') gibt.

Warnung 1:  Eine bijektive, stetige Abbildung ist nicht immer ein Homöomorphismus. Ganz allgemein muss man aufpassen:  Ist f eine stetige Abbildung, so ist das Bild einer offenen Menge nur selten wieder offen! Es gibt viele Beispiele:  Sei (X,T) ein topologischer Raum und T' eine Teilmenge von T, so dass auch (X,T') wieder ein topologischer Raum ist. Dann ist die identische Abbildung id: (X,T) → (X,T') stetig. Ist aber T' eine echte Teilmenge von T, so ist die Umkehrabbildung nicht stetig! e2πix: [0,1[ → S1. (Andere Beschreibung:  Sei I = [0,1], und betrachte die Quotienten-Abbildung p:I → I/~, die die Endpunkte von I identifiziert. Die Einschränkung von p auf [0,1[ ist bijektiv und stetig, ihre Umkehrabbildung ist aber nicht stetig.)

Warnung 2:  Die Existenz surjektiver stetiger Abbildungen X → Y, Y → X impliziert nicht, dass X und Y topologisch äquivalent sind. Beispiel:  Eine Peano-Kurve ist eine surjektive stetige Abbildung I → I×I. Und natürlich gibt es surjektive stetige Abbildungen I×I → I. Aber I und I×I sind nicht topologisch äquivalent. (Entfernt man einen beliebigen Punkt aus I×I, so bleibt der Raum zusammenhängend; entfernt man dagegen aus I den Punkt 1/2, so erhält man zwei Zusammenhangskomponenten.)

Abgeleitete Begriffe: 

• Eine Teilmenge A von X heißt abgeschlossen, falls A das Komplement einer offenen Menge ist.
• Umgebung: 
  Sei x in X. Eine Teilmenge U von X heißt Umgebung von x, wenn es eine offene Menge O gibt mit x in O und O enthalten in U.

• Sei Y eine Teilmenge von X, sei x ein Element von X. Man nennt
  • x einen inneren Punkt von Y, falls Y eine Umgebung von x ist.
  • x einen äußeren Punkt von Y, falls das Komplement von Y eine Umgebung von x ist.
  • einen Randpunkt von Y, falls weder Y noch das Komplement von Y Umgebung von x ist.
    Genau dann ist y Randpunkt von Y, wenn jede offene Menge, die y enthält, sowohl Y als auch das Komplement von Y schneidet.

• Sei Y eine Teilmenge von X.
  • Der Abschluss einer Teilmenge Y ist die Menge aller Punkte x von X, die innere Punkte oder Randpunkte von Y sind.
  • Der offene Kern von Y ist die Menge aller inneren Punkte von Y.
  • Der Rand von Y ist die Menge aller Randpunkte von Y.
  Notation: 
  

Warnung:  Wenn vom Abschluss, vom offenen Kern und vom Rand einer Menge Y gesprochen wird, so muss man immer wissen, in welchem topologischen Raum X man sich befindet! Auch die Notationen verzichten darauf, X zu erwähnen - doch die Kenntnis von X ist unabdingbar! Beispiel:  Betrachte das Intervall I = [0,1] als Y. Ist X = Y, so ist der offene Kern von Y ganz Y. Ist X = R, so ist der offene Kern von Y das offene Intervall ]0,1[. Ist X = R2 (und Y die Menge der Paare der Form (x,0) mit x in I - auch diese Menge wird man manchmal einfach mit I identifizieren), so ist der offene Kern von Y die leere Menge!

---

Weitere Begriffsbildungen werden später diskutiert: 

	siehe
Trennungseigenschaften	Abschnitt 2
Abzählbarkeitseigenschaften	SPÄTER
Kompaktheit	Abschnitt 2

Axiomatik

• Offene Mengen
  Axiome:  siehe oben
• Abgeschlossene Mengen.
  Axiome:  Gegeben ist (X,A), dabei ist X eine Menge und A eine Menge von Teilmengen von X mit: 
  • Die leere Menge {} und die Menge X selbst gehören zu A.
  • A ist abgeschlossen unter beliebigen Durchschnitten.
  • A ist abgeschlossen unter endlichen Vereinigungen.
• Umgebungssystem (X,U(x))
  Axiome:  U ordnet jedem x in X eine nicht-leere Menge U(x) von Teilmengen von X zu mit: 
  • Ist V in U(x), so ist x Element von V.
  • Ist V in U(x) und ist V in W enthalten, so ist auch W in U(x).
  • U(x) ist abgeschlossen unter endlichen Durchschnitten.
  • Zu V in U(x) gibt es eine Untermenge V' von V, die zu U(x) gehört, so dass V' für jedes y in V' zu U(y) gehört.
• Abschluss-Operator (X,c)
  Axiome:  X ist eine Menge, c eine Abbildung der Potenzmenge von X in sich mit
  • c({}) = {}
  • Für jede Teilmenge Y von X ist Y in c(Y) enthalten.
  • Für jede Teilmenge Y von X gilt c(c(Y)) = Y.
  • Ist Y die Vereinigung von Y₁ und Y₂, so ist c(Y) die Vereinigung von c(Y₁) und c(Y₂).

  ---

  Beweise, dass es sich um äquivalente Axiomensysteme handelt; zum Beispiel: 
  1. Sei (X,T) topologischer Raum. Sei u(T)(x) die Menge der Umgebungen von x. Dann erfüllt (X;u(T)) die Axiome eines Umgebungssystems.
       (Zu zeigen ist, dass die Axiome erfüllt sind).
  2. Sei (X,U) ein Umgebungssystem. Sei t(U) die Menge aller Teilmengen von X mit ... . Dann ist (X,t(U)) ein topologischer Raum.
       (Zu zeigen ist, dass die Axiome erfüllt sind).
  3. T = t(u(T)).   (Zu zeigen sind zwei Inklusionen.)
  4. U = u(t(U)).   (Zu zeigen sind zwei Inklusionen.)

  ---

  Beachte:  Arbeitet man mit dem Axiomensystem für offene Mengen (wie wir es tun), so hat der jeweils erste Beweisschritt den Charakter von Sätzen, Lemmata, Merkregeln, die man wissen muss - die weiteren Beweisschritte dagegen erscheinen überflüssig. Sie dienen nur dazu zu betonen, dass man die ganze Theorie auch in eine andere Sprache übersetzen kann...

  Beispiel für derartige Merkregeln:  Der Abschluss-Operator ist idempotent: 
  
  (Also:  Der Abschluss einer beliebigen Teilmenge ist abgeschlossen.)

  Beweis:  Zu zeigen ist, dass der Rand des Abschlusses von Y im Rand von Y enthalten ist ....

  ---

Beispiele

Trivialste (und ganz untypische) Beispiele:  Sei X eine Menge.
• Es ist {{},X} eine Topologie, man nennt sie die "grobe" Topologie. (Die einzigen offenen Mengen sind also die leere Menge und X selbst.)
• Die Potenzmenge von X ist ebenfalls eine Topologie, man nennt sie die "diskrete" Topologie. (In diesem Fall ist also jede Untermenge von X offen.)

1. Standard-Beispiele.

   Wir notieren jeweils nur die Grundmenge, und zwar Teilmengen eines Rⁿ. Dabei werde Rⁿ wie üblich als metrischer Raum aufgefasst, wobei die Metrik durch die euklid'sche Norm definiert ist (siehe auch Beispiel D.). Als metrischer Raum ist Rⁿ (und jede Untermenge) ein topologischer Raum, siehe C. Dies ist die Topologie, die gemeint ist! Verwiesen sei auch auf den Abschnitt "Konstruktionen, um neue Räume zu gewinnen", und dort auf die erste Konstruktion:  "Unterraum".

   Die "Topologie" des Rⁿ ist also die aus der Vorlesung "Analysis" bekannte "Topologie" (wie oben notiert, versteht man unter der "Topologie" eines Raums X die Menge der offenen Teilmengen...)

   • Die reellen Zahlen R, allgemeiner:  Rⁿ.
   • Das Einheitsintervall I = [0,1]

     ---

   • n-Ball, n-Würfel, n-Simplex: 
     

     ---

   • Ganz wichtig:  die n-Sphäre: 
     
     die n-Sphäre ist der Rand des n-Balls; entsprechend kann man den Rand des n-Würfels und den des n-Simplexes betrachten.

     ---

     Beispiel für topologische Äquivalenzen: 
     Satz. Für jedes n sind n-Ball, n-Würfel und n-Simplex topologisch äquivalent

     Hier einer der Beweisschritte für n=2: 
     

     Später werden wir sehen:  Sind n und n' verschieden, so ist der n-Würfel nicht zum n'-Würfel topologisch äquivalent. Zumindest für n'=1 und n>1 ist der Beweis einfach. (Der 1-Würfel besitzt Punkte x, so dass das Komplement nicht zusammenhängend ist. Ist n mindestens 2, so ist das Komplement eines jeden Punkts des n-Würfels zusammenhängend.)

     ---

2. Endliche Räume
   Beispiel:  Auf einer zwei-elementigen Menge X gibt es genau 4 Topologien. Sei X = {a,b}; es gibt 4 Teilmengen, nämlich {}, {a},{b},{a,b}, also 2⁴ = 16 Mengen von Teilmengen, von denen vier eine Topologie liefern; mit x markieren wir die Teilmengen, die zur Topologie gehören: 

   Topologie	{}	{a}	{b}	{a,b}
   grob	x			x
   T'	x	x		x
   T"	x		x	x
   diskret	x	x	x	x

   Die Topologien T' und T'' liefern topologisch äquivalente Räume:  vertausche a und b. Also gilt:  Bis auf topologische Äquivalenz gibt es genau drei topologische Räume mit zweielementiger Grundmenge.

3. Metrische Räume
   Eine Metrik auf einer Menge X ist eine Abbildung
   
   mit
   • Genau dann ist d(x,y) = 0, wenn x = y gilt.
   • d(x,y) = d(y,x)
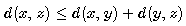   • ("Dreiecksungleichung")
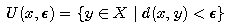   Ist d eine Metrik auf X, so nennt man (X,d) einen metrischen Raum.
   In einem metrischen Raum betrachtet man für jedes x in X und jede Zahl ε > 0 die offene Kugel
   .
   Man nennt eine Teilmenge O von X offen, falls sie mit jedem x eine offene Kugel U(x,ε) enthält.

   Satz. Ist (X,d) ein metrischer Raum, so bilden die offenen Mengen eine Topologie.

   Die meisten Räume, die wir betrachten werden, besitzen zwar eine Metrik (sind also metrische Räume), wir werden dies aber nur selten ausnutzen. Allerdings gibt es zwei Argumentationsweisen, bei denen wir die Existenz einer Metrik verwenden werden: Die Existenz einer Lebesgue-Zahl einer offenen Überdeckung eines kompakten (metrischen) Raums. Das Arbeiten mit gleichmäßig konvergenten Folgen stetiger Funktionen. (Hier weiß man, dass der Limes existiert und wieder stetig ist.)

4. Normierte Vektorräume
   Eine Norm auf einem reellen Vektorraum V ist eine Abbildung
   || - ||: V → {r ∈ R| r ≥ 0}
   mit
   • Genau dann ist ||v||=0, wenn v=0.
   • ||λ v|| = |λ| ||v|| für alle λ ∈ R und alle v ∈ V.
   • ||v+w|| ≤ ||v|| + ||w|| für alle v,w ∈ V.
   Eine Norm || - || auf einem reellen Vektorraum liefert durch d(x,y):= ||x-y|| eine Metrik d, also eine Topologie.
   Die euklid'sche Norm des Rⁿ wird in diesem Leitfaden meist mit | - | bezeichnet (Es ist also |(x₁,...,x_n)| = Wurzel aus (∑_i x_i²).)
5. Funktionenräume
   Viele Funktionenräume sind normierte Vektorräume, besitzen also eine Metrik und demnach eine Topologie.
   Oft arbeitet man mit einer Menge von Halbnormen; auch dies liefert eine Topologie.

Konstruktionen, um neue Räume zu gewinnen: 

• Unterraum: 
  Jede Untermenge Y eines topologischen Raums X = (X,T) ist selbst ein topologischer Raum mit der "induzierten Topologie"; die offenen Mengen von Y sind die Durchschnitte der offenen Mengen in T mit Y.

  Beispiel:  Sei X = R und Y = I = [0,1], das Einheitsintervall. Betrachte Y als Raum mit der "induzierten Topologie". Wie sehen die offenen Mengen von Y aus? Zum Beispiel ist [0,1/2[ eine offene Menge!

  Weiteres zu den Unterräumen.

• Quotientenraum

• Summe (disjunkte Vereinigung) zweier topologischer Räume: 
  Seien (X₁,T₁) und (X₂,T₂) topologische Räume. Die disjunkte Vereinigung von X₁ und X₂ wird ein topologischer Raum, wenn man als offene Mengen die disjunkten Vereinigungen von Mengen in T₁ und in T₂ nimmt, man nennt diesen Raum die Summe der beiden Räume und schreibt manchmal (X₁,T₁)+(X₂,T₂).

  Eine Charakterisierung der topologischen Summen erfolgt im Rahmen der Diskussion des Begriffs des Zusammenhangs.

  Es gilt (trivialerweise):
  Lemma. Seien X und Y topologische Räume und X+Y ihre Summe.

  • Die kanonischen Inklusionen u_X: X → X+Y und u_Y: Y → X+Y sind stetig.
  • Ist Z ein topologischer Raum und sind f : X → Z und g : X → Z stetige Abbildungen, so ist die Abbildung h:X+Y → Z mit h(x) = f(x) für x in X und h(y) = g(y) für y in Y stetig.

• Produkt zweier topologischer Räume:
  Seien X und Y topologische Räume. Das mengentheoretische Produkt X × Y (also die Menge aller Paare (x,y) mit x in X und y in Y) wird auf folgende Weise zu einem topologischen Raum: Eine Teilmenge W in X × Y heißt offen, wenn es zu jedem Punkt (x,y) in W eine offene Menge U in X mit x in U und eine offene Menge V in Y mit y in V gibt, so dass U × V in W enthalten ist. Man nennt die so definierte Topologie die Produkt-Topologie. Schreibt man X × Y, so geht man immer davon aus, dass die Produkt-Topologie gemeint ist; sie ist durch folgende "universelle Eigenschaft" eindeutig bestimmt:

  Lemma. Seien X und Y topologische Räume und X×Y das Produkt.

  • Die kanonischen Projektionen p_X: X×Y → X und p_Y: X×Y → Y sind stetig.
  • Ist Z ein topologischer Raum und sind f : Z → X und g : Z → Y stetige Abbildungen, so ist die Abbildung Z → X×Y, die z auf (f(z),g(z)) abbildet, stetig.