Information on the Picture

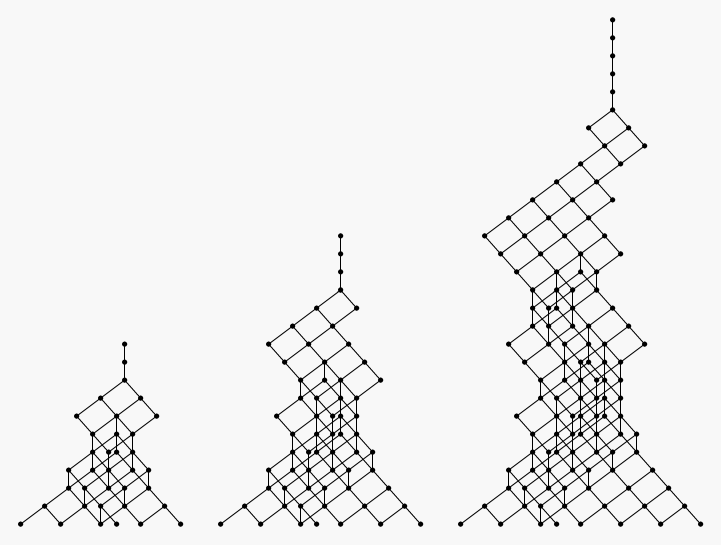
The picture epitomises the categories of representations of Dynkin quivers of type E₆, E₇ and E₈. More precisely, the vertices correspond to the indecomposable representations whereas the edges indicate the product order on the set of dimension vectors.

Gabriel's theorem asserts that a connected quiver admits (up to isomorphism) only finitely many indecomposable representations if and only if it is an orientation of a Dynkin diagram of type A, D or E. Furthermore, the dimension vectors of the indecomposable representations are in bijection with the positive roots of the corresponding simple Lie algebra. In other words, the picture shows the Hasse diagrams of the positive parts of the root systems of type E₆, E₇ and E₈.

In each case, the simple representations form an antichain of length n, where n is the number of vertices in the quiver. Ringel [R] has studied antichains of length n-1. Especially, there is a unique maximal antichain of length n-1. For the quiver E₇ the indecomposable representations of dimension 5 form an antichain of length 6.

[R] Claus Michael Ringel: The (n-1)-antichains in a root poset of width n. Preprint: arXiv:1306.1593.

Please see here for another characteristic picture.