Freezing Method -- Decompose and Freeze Method -- Comsol Multiphysics
| Fakultät für Mathematik |
|
|
NavigationAktuellKonferenzen |
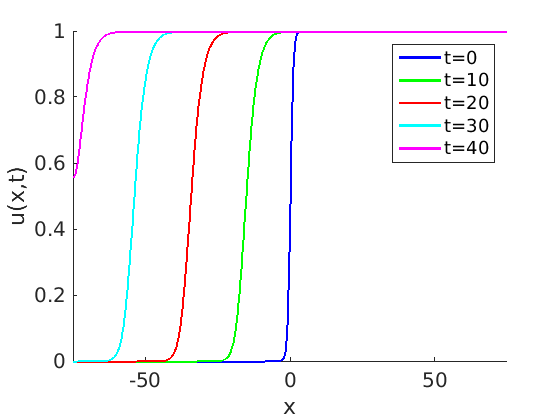
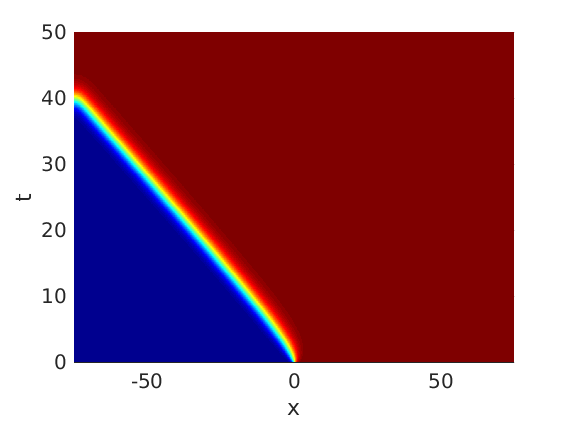
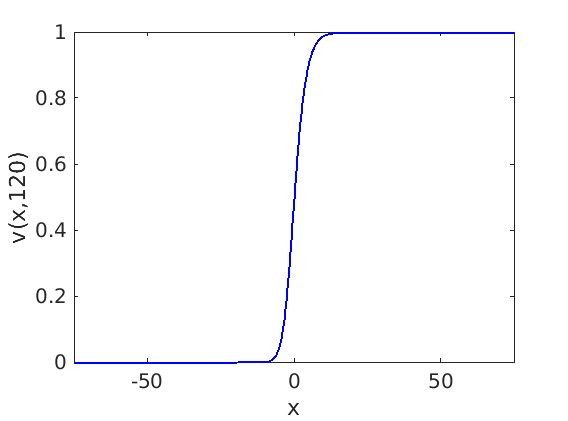
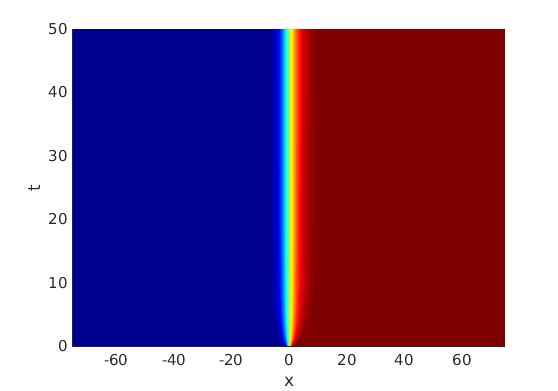
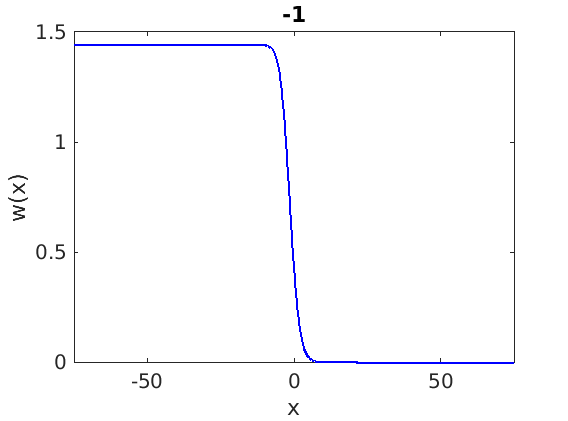
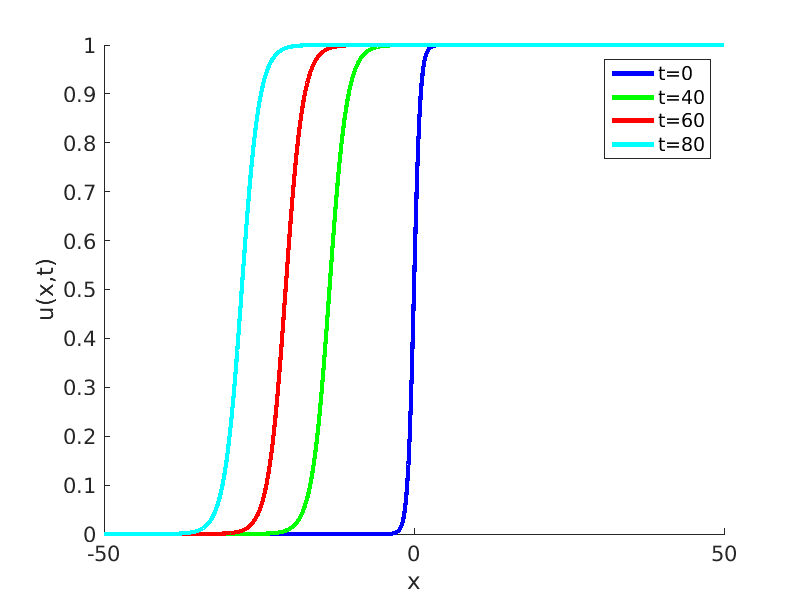
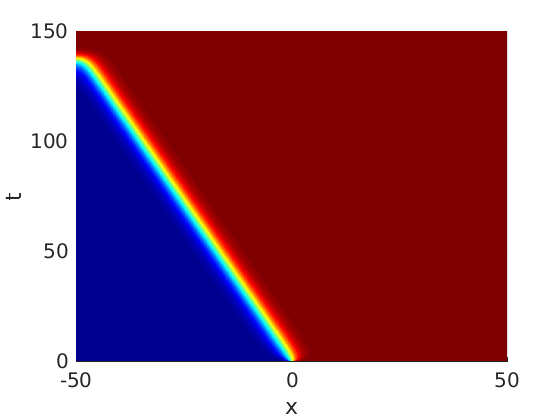
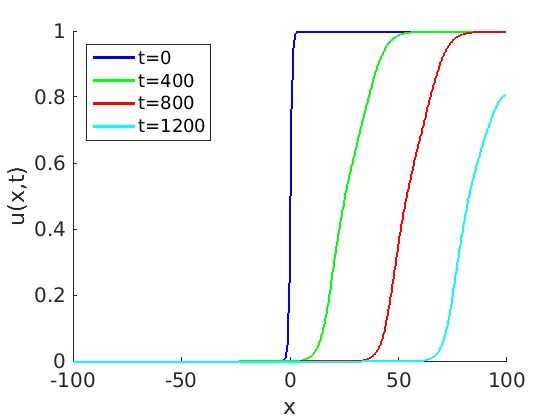
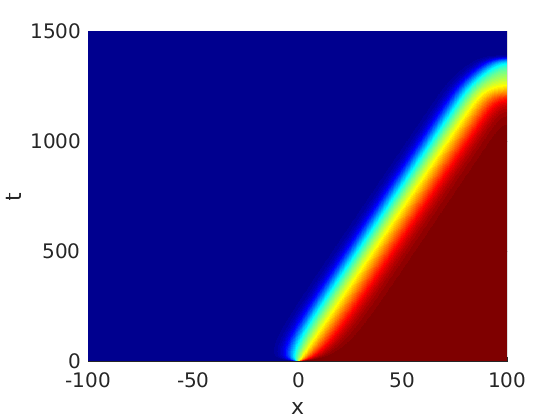
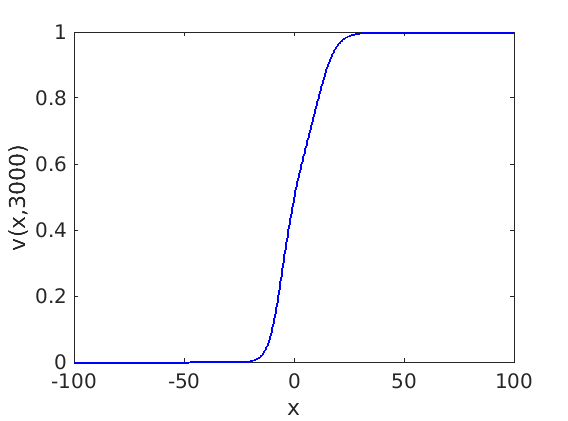
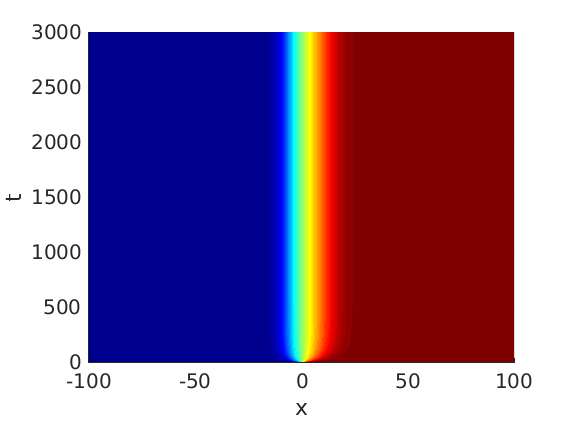
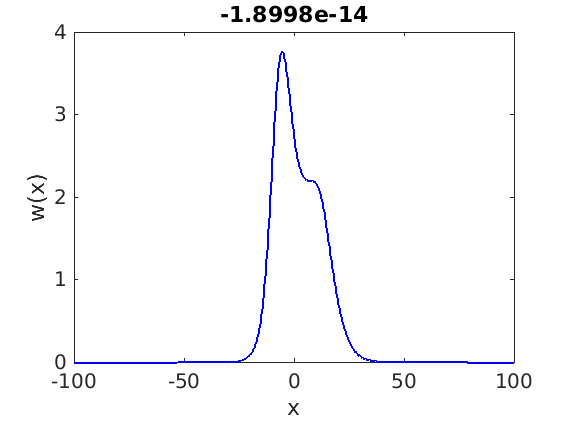
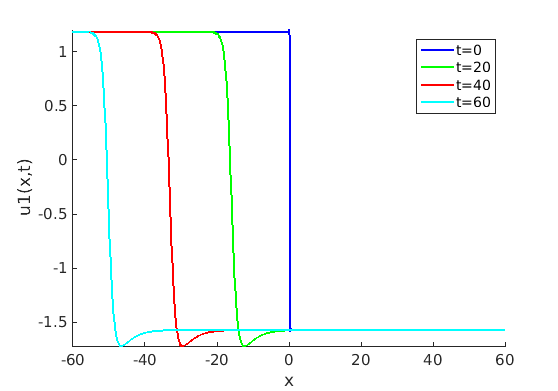
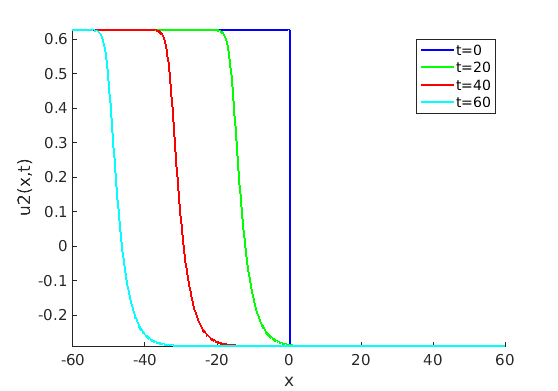
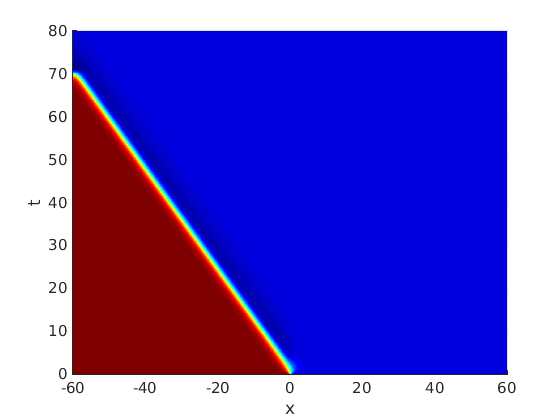
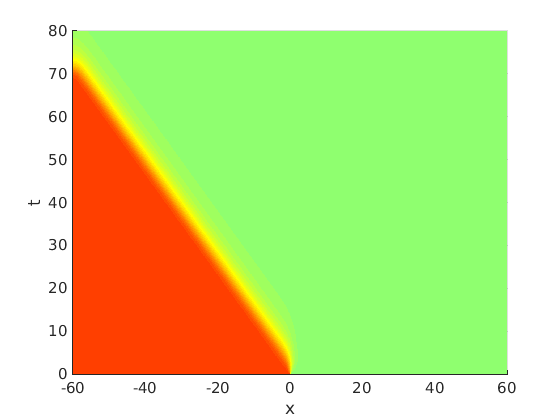
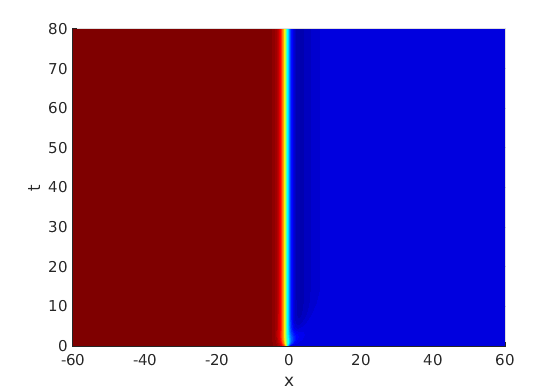
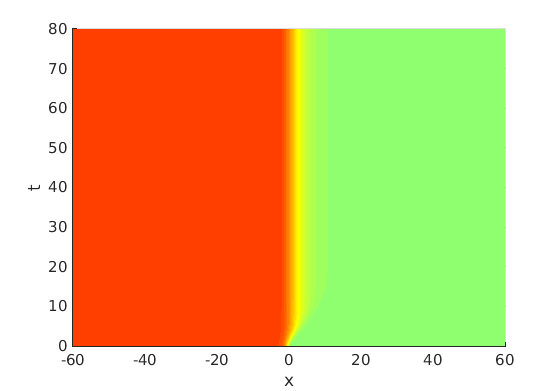
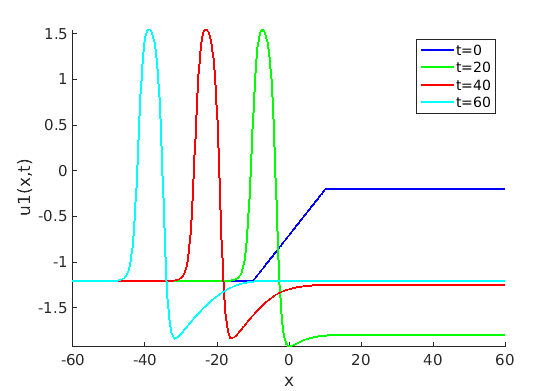
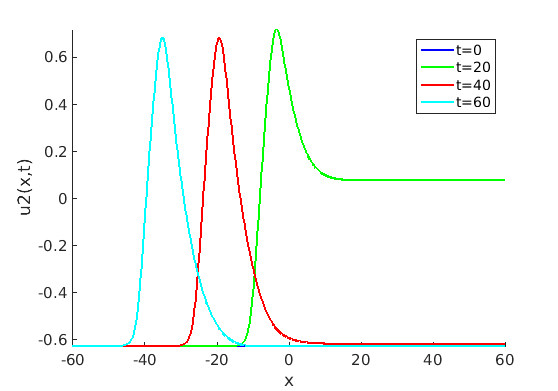
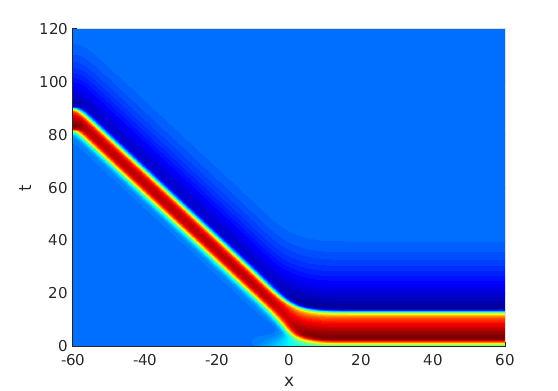
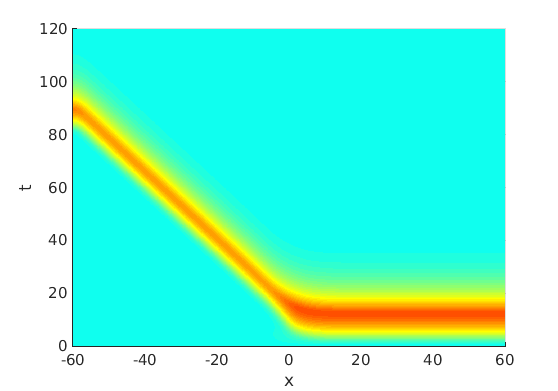
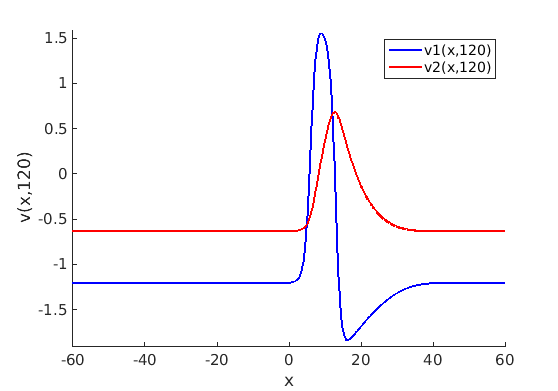
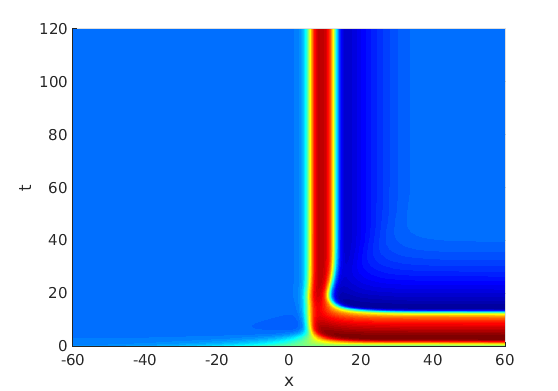
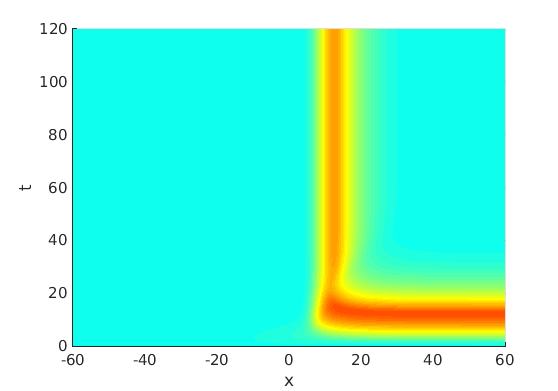
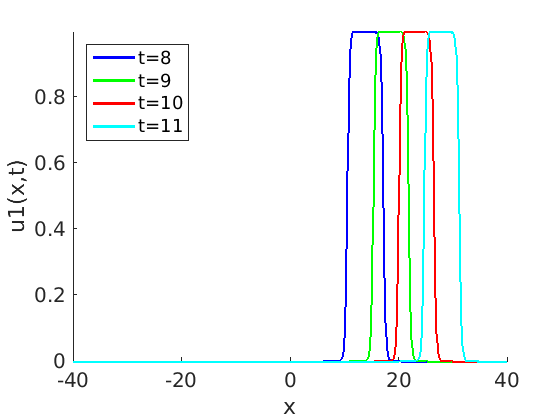
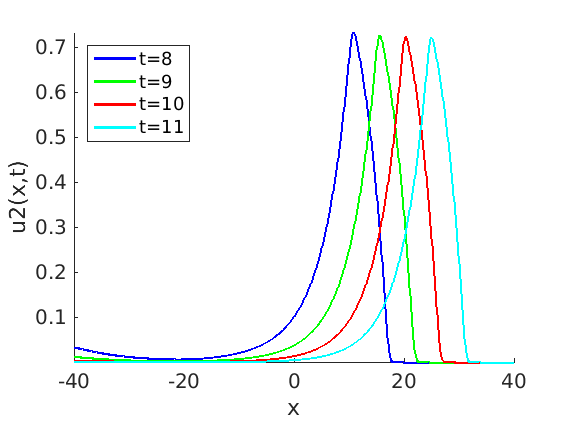
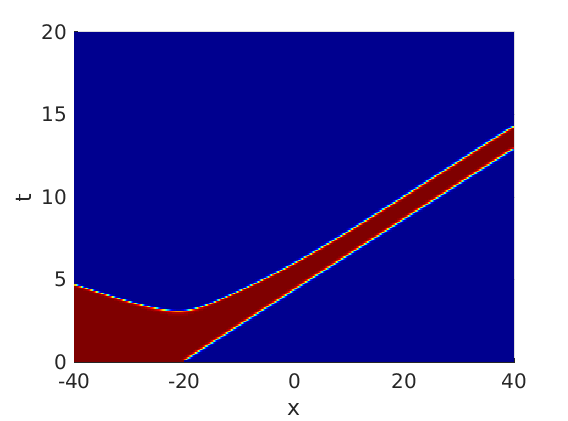
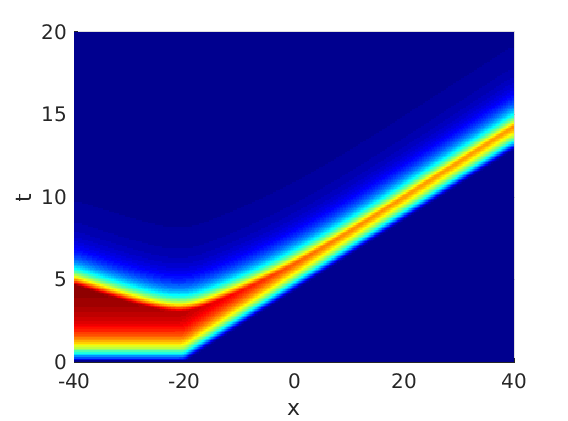
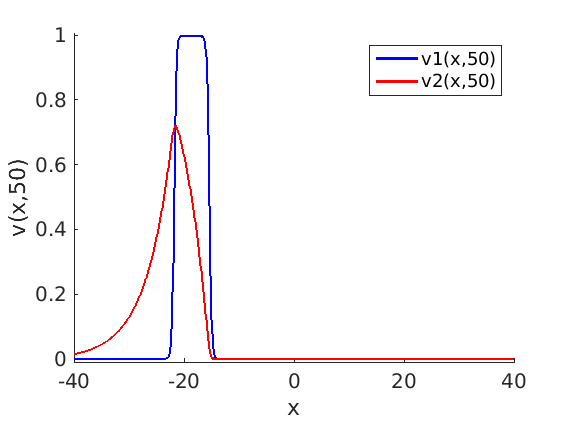
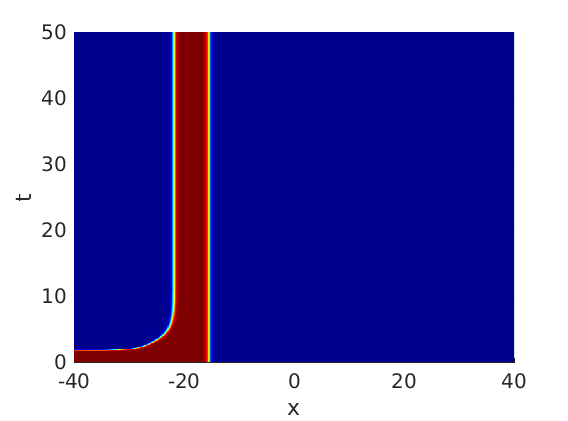
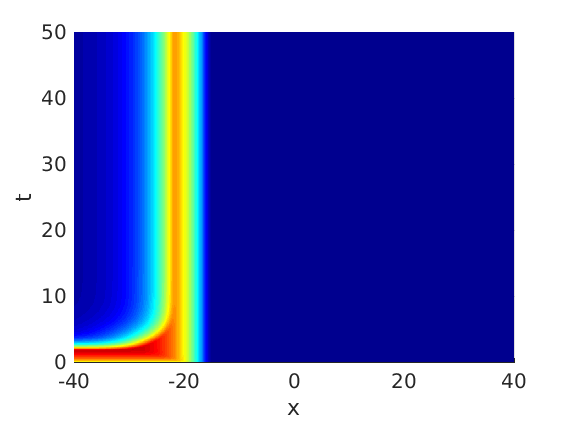
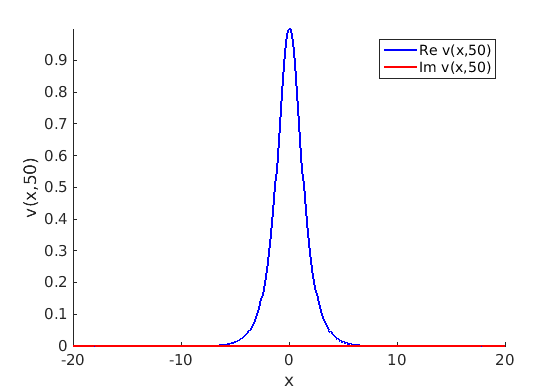
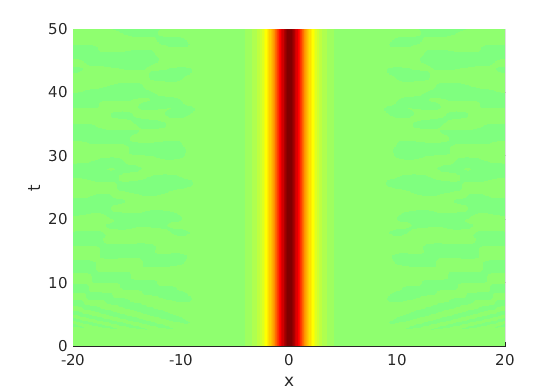
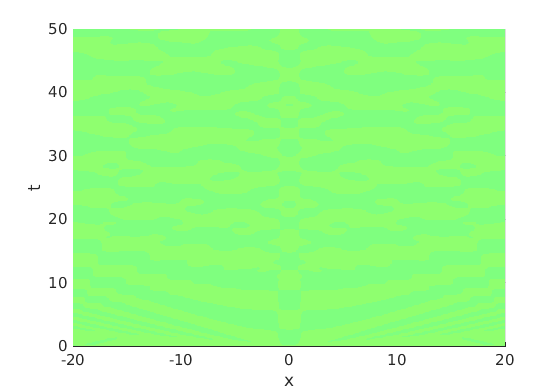
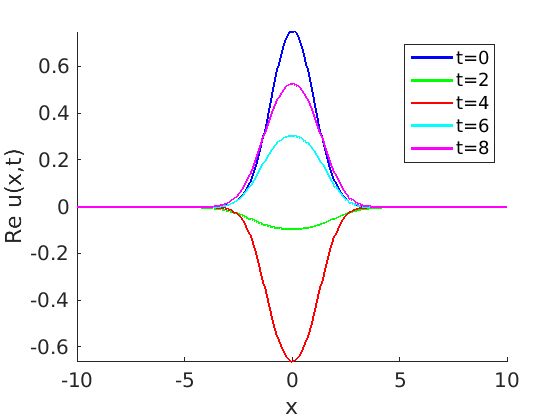
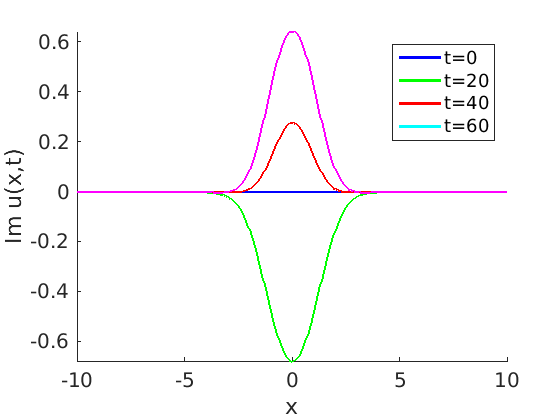
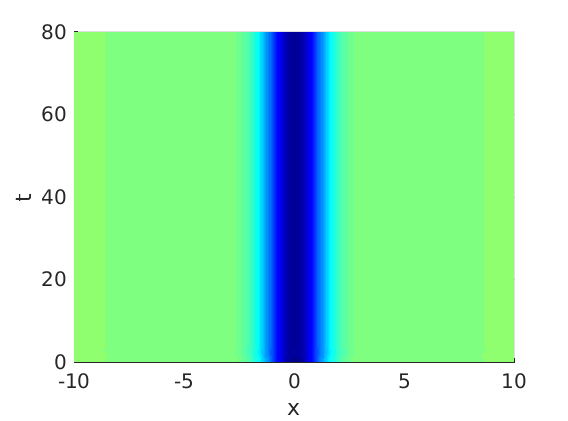
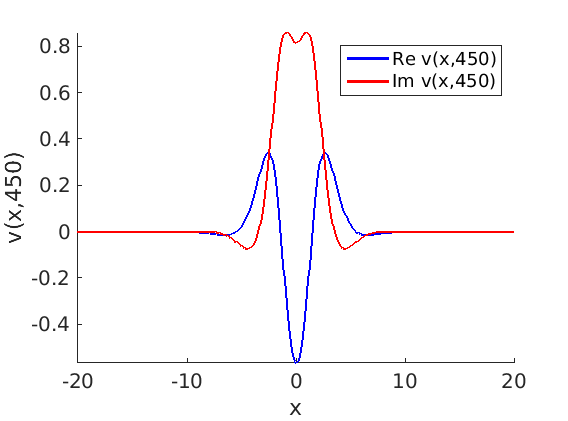
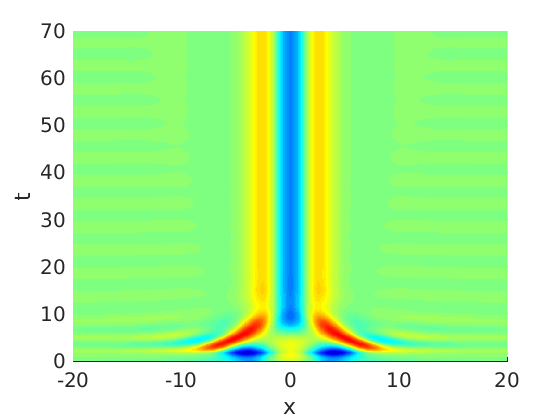
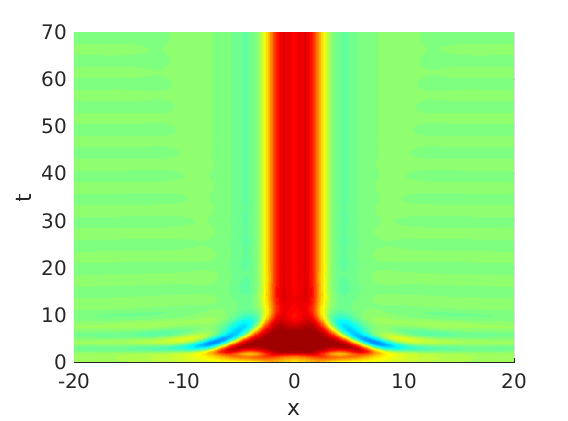
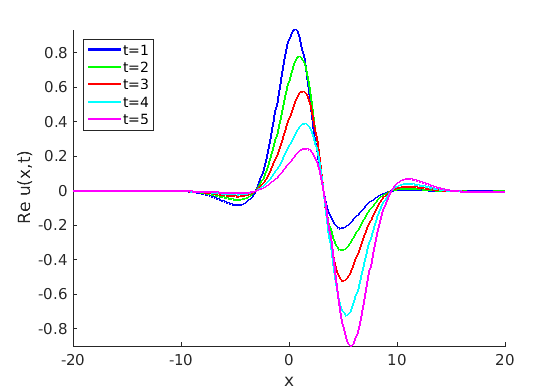
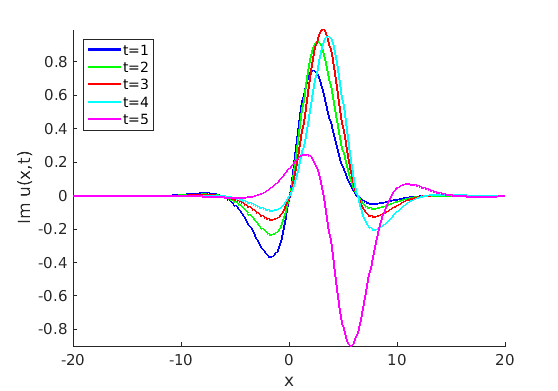
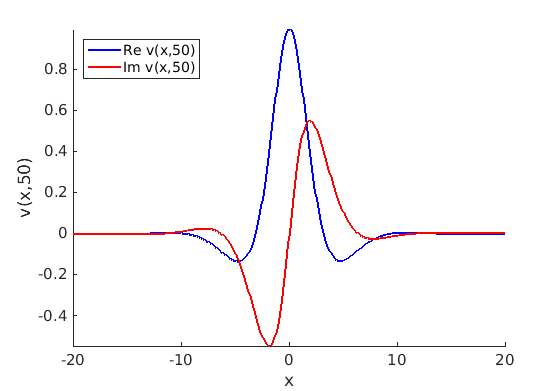
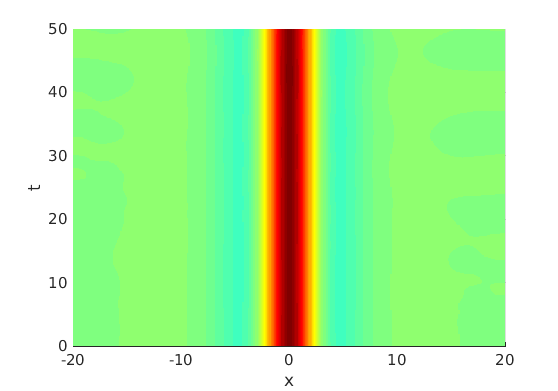
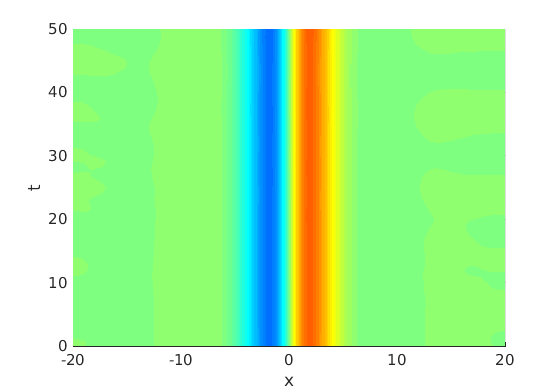
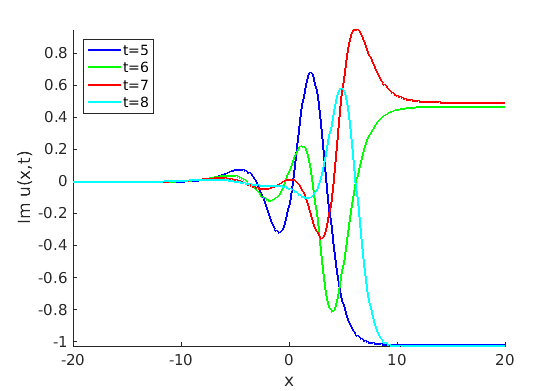
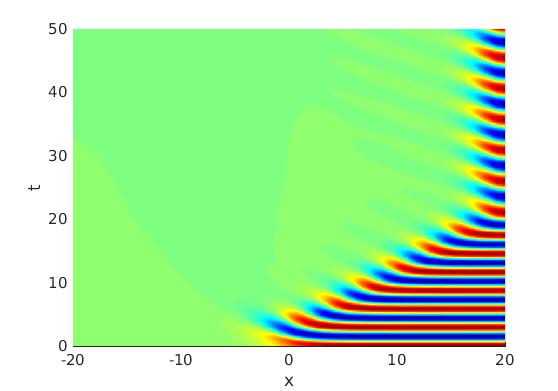
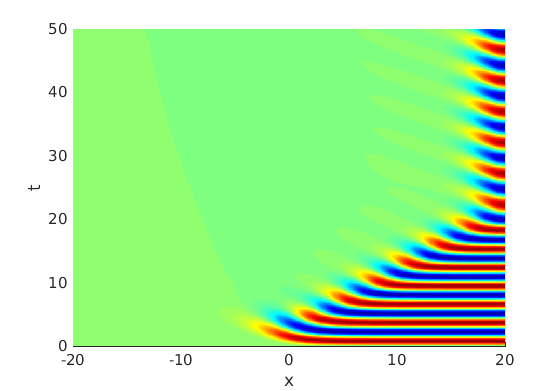
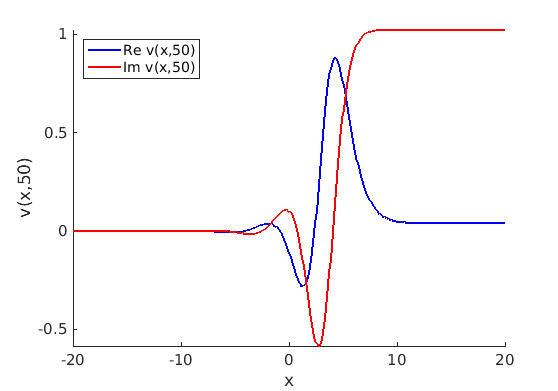
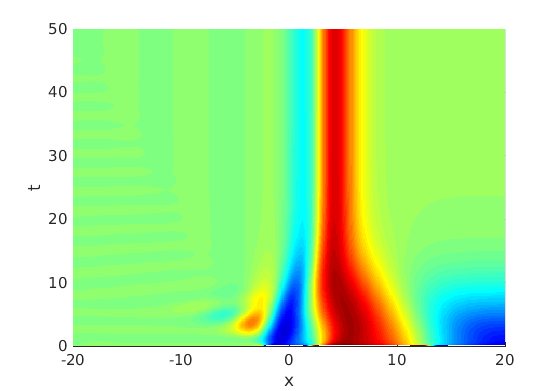
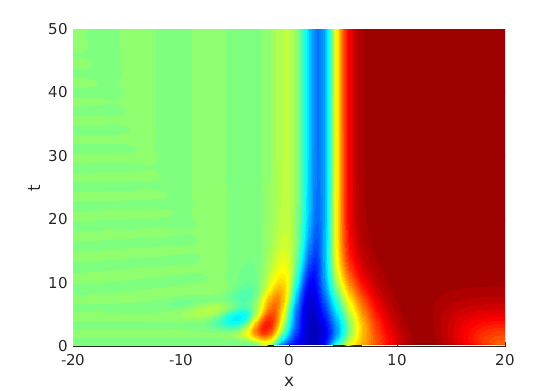
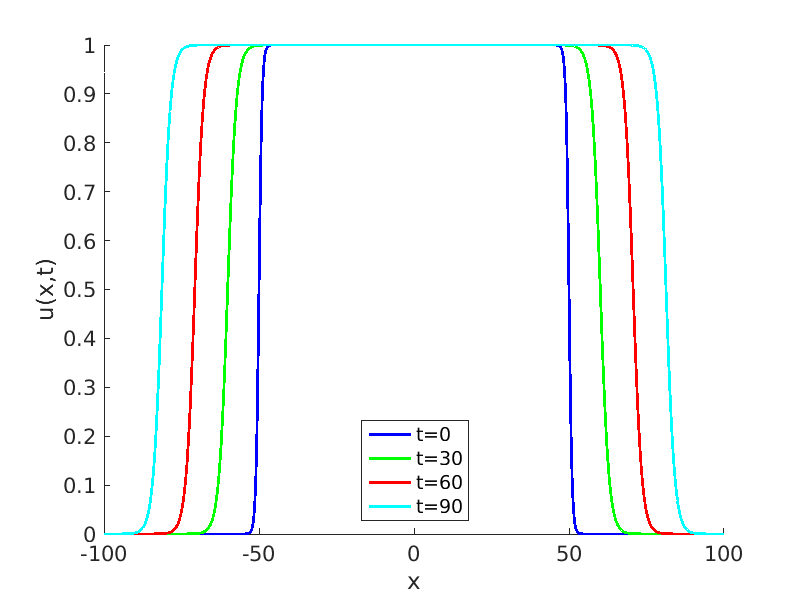
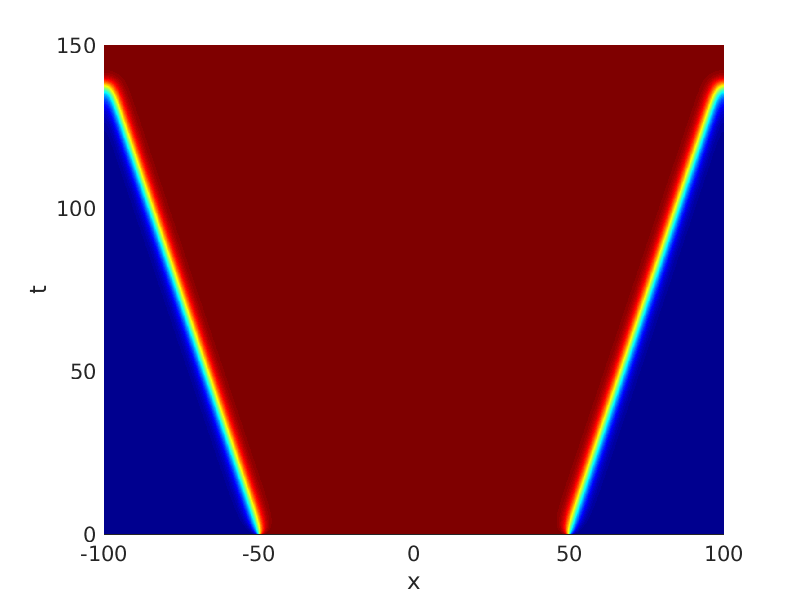
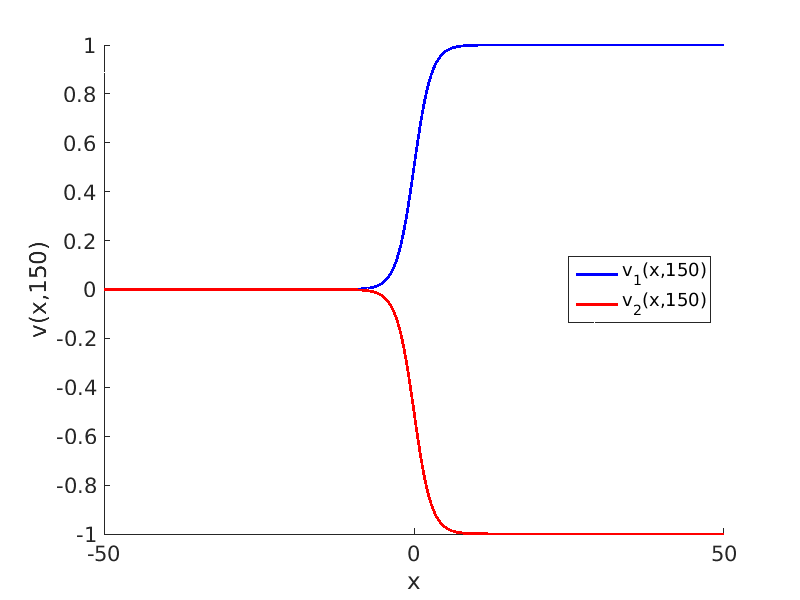
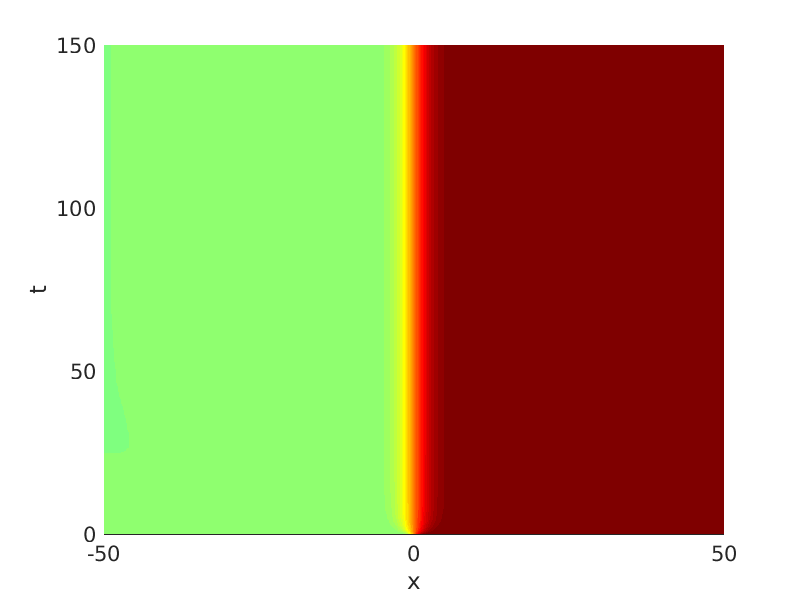
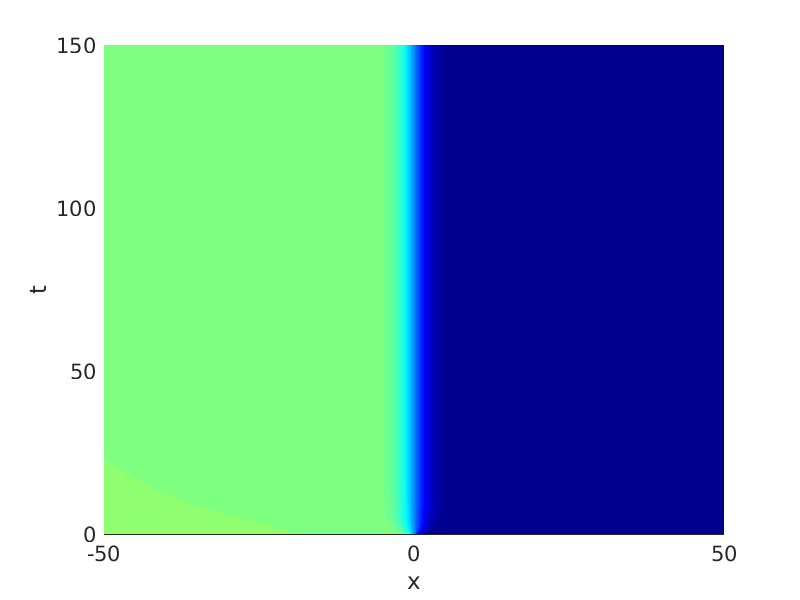
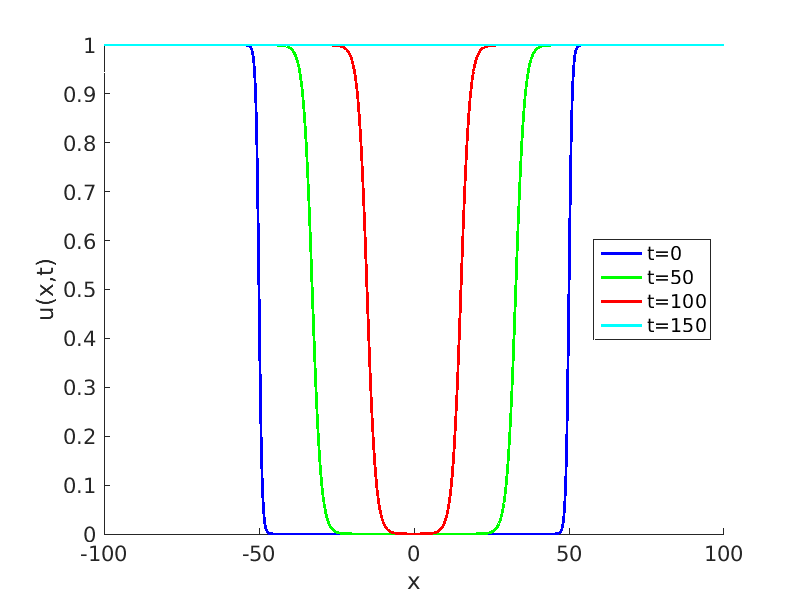
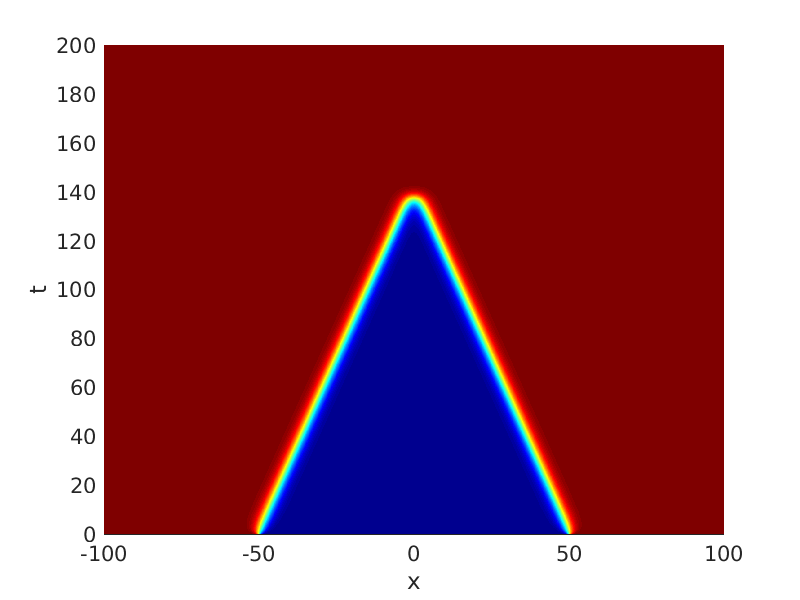
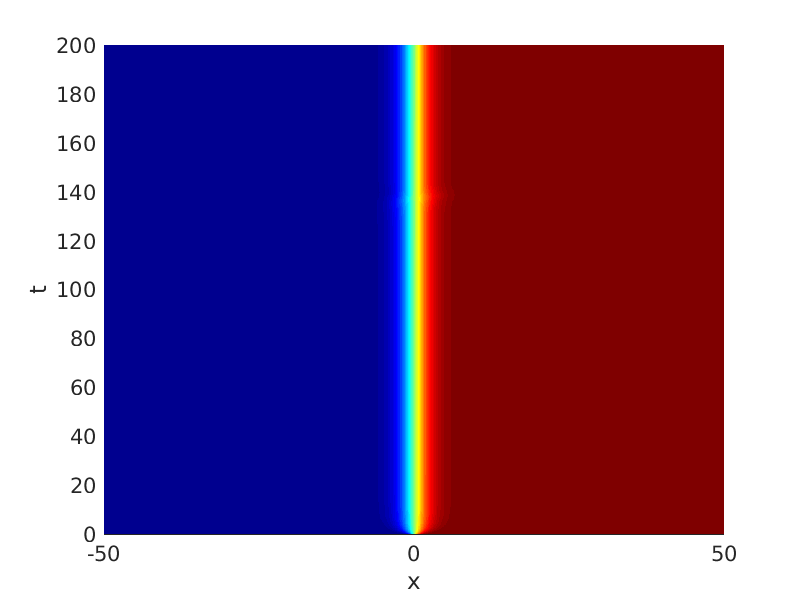
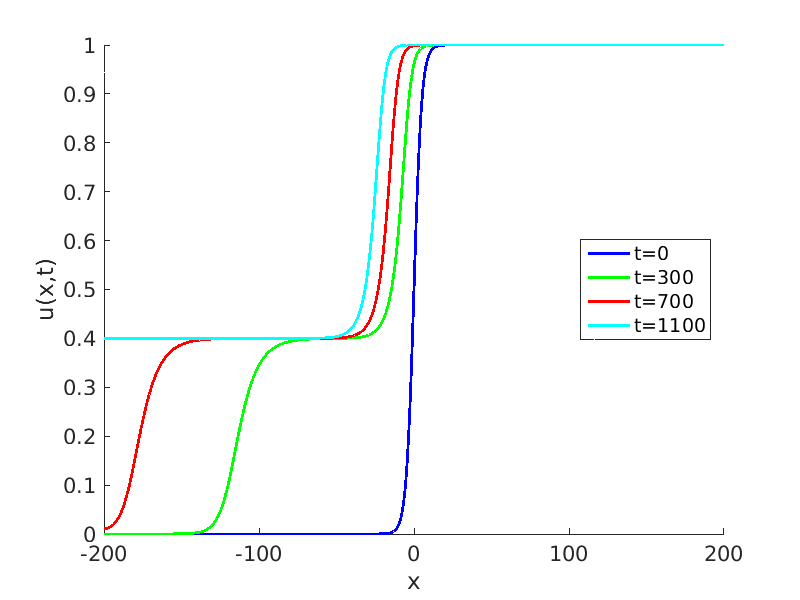
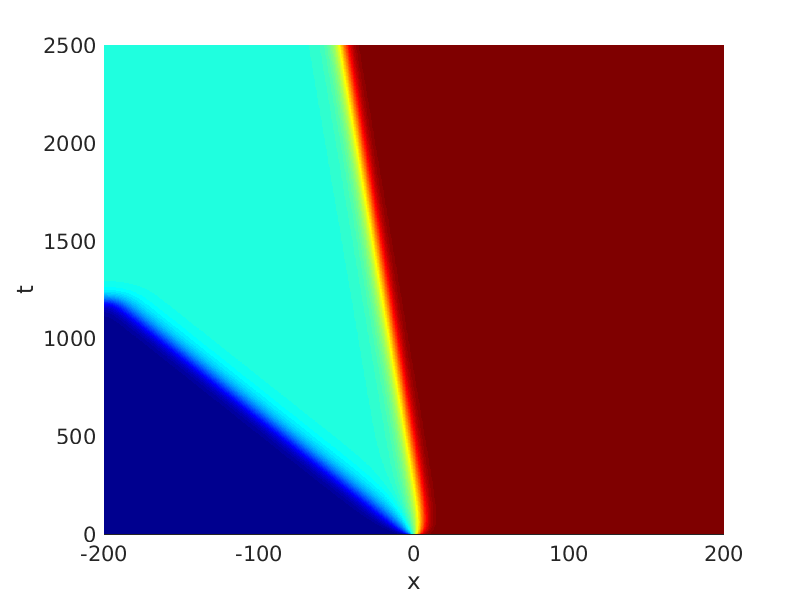
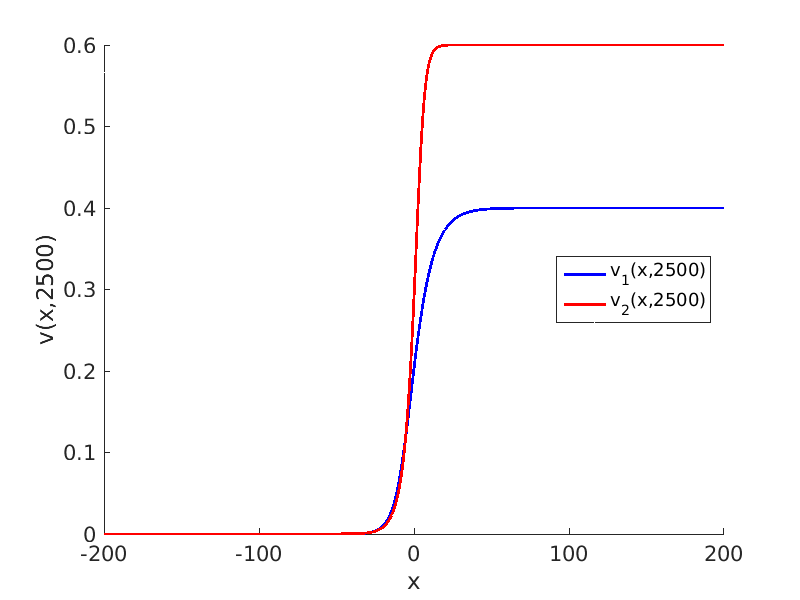
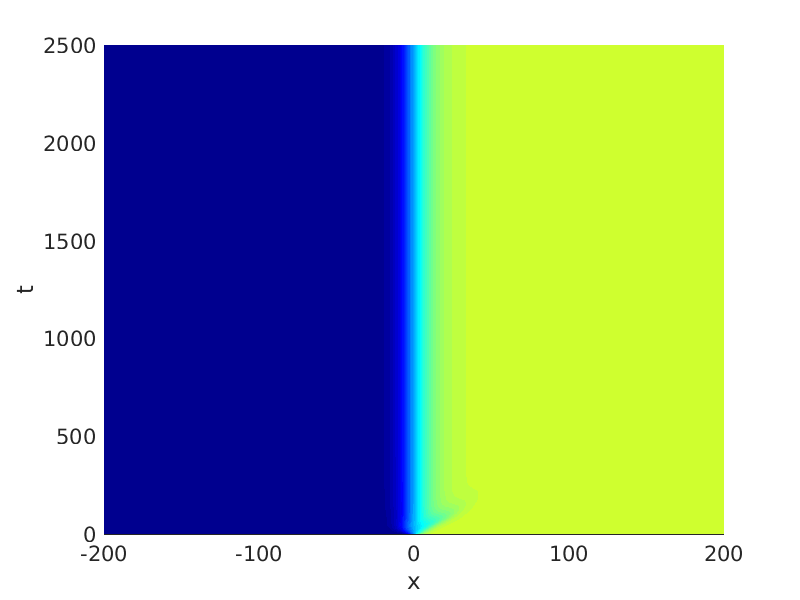
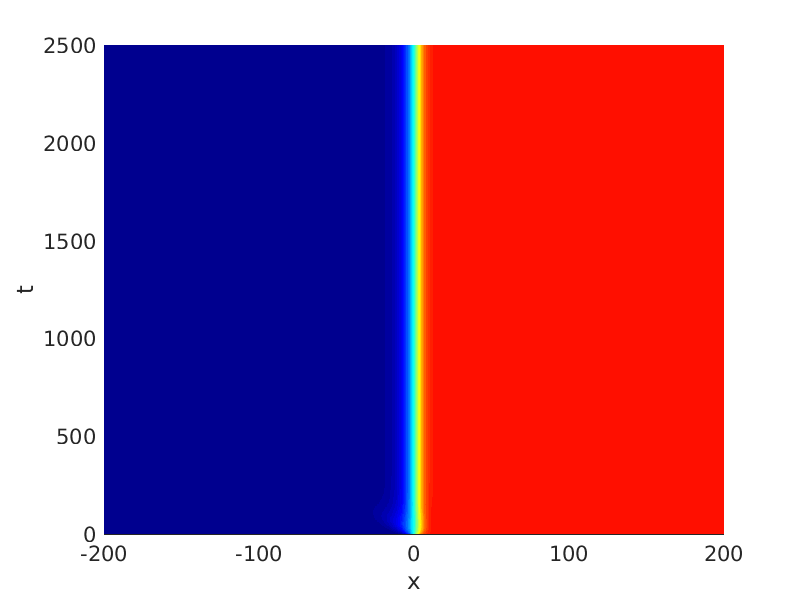
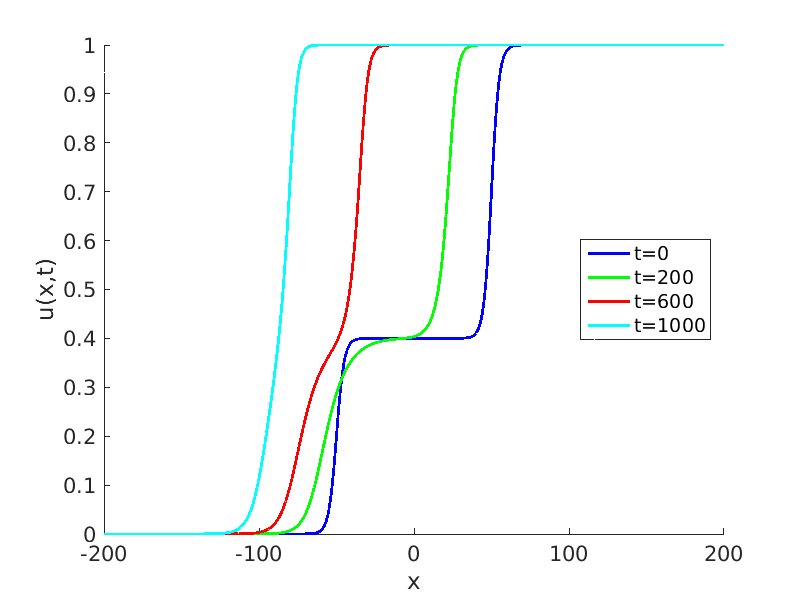
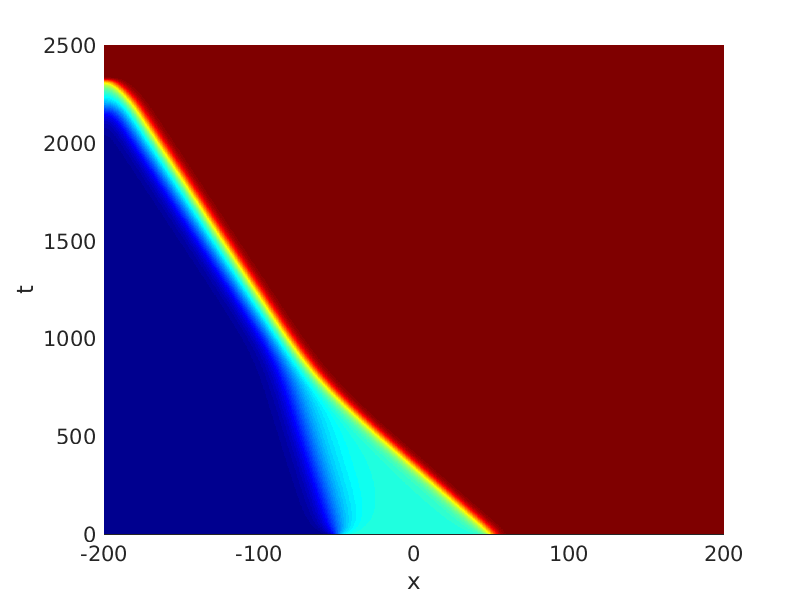
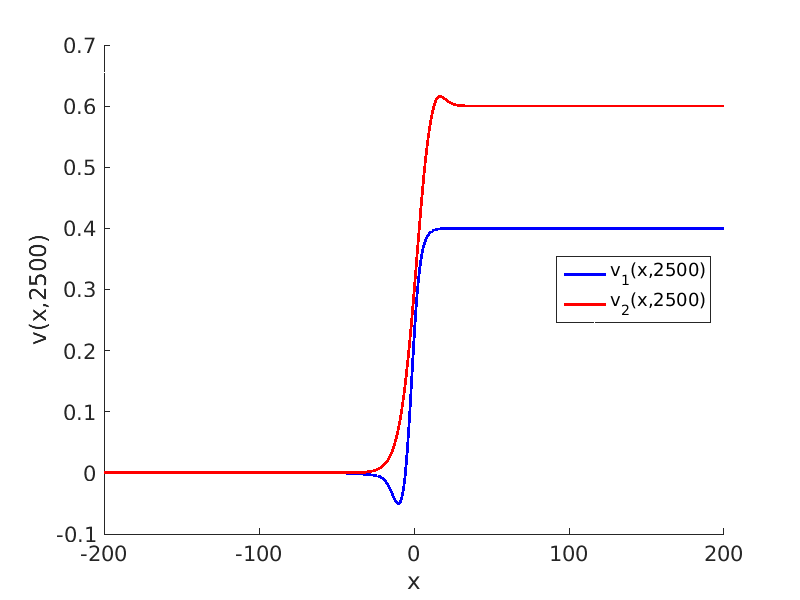
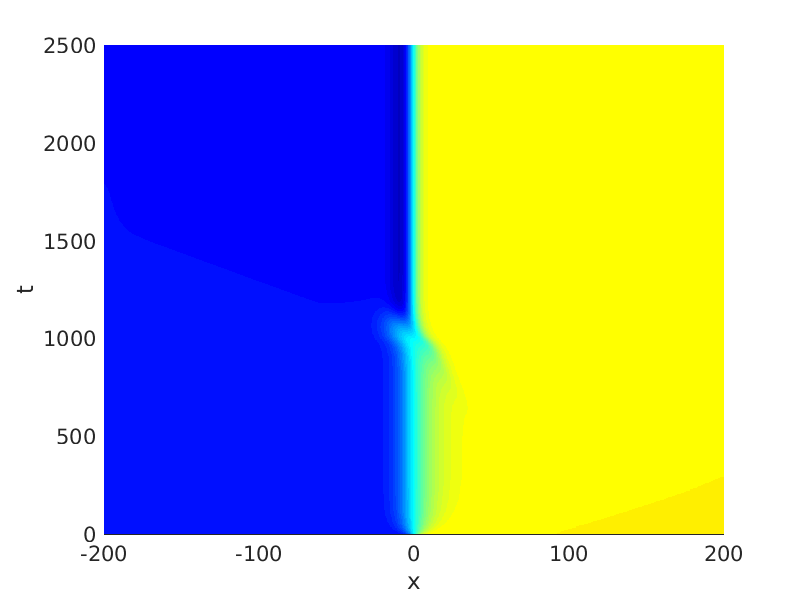
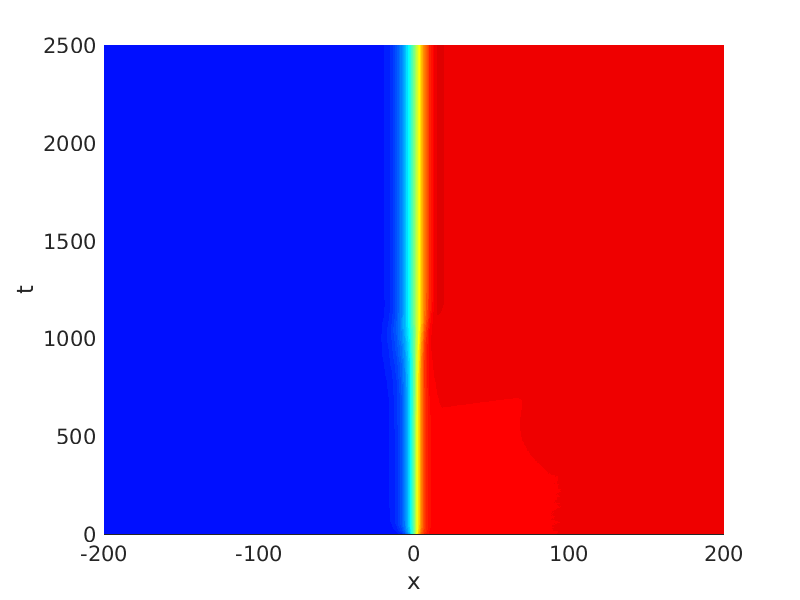
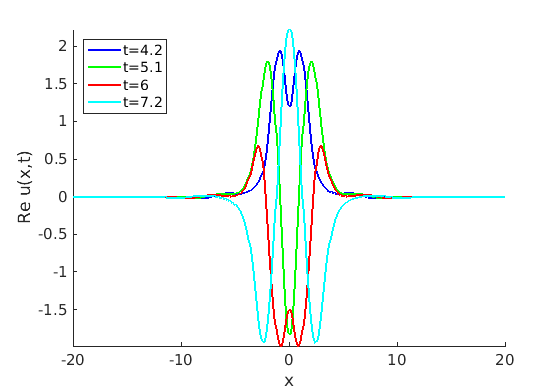
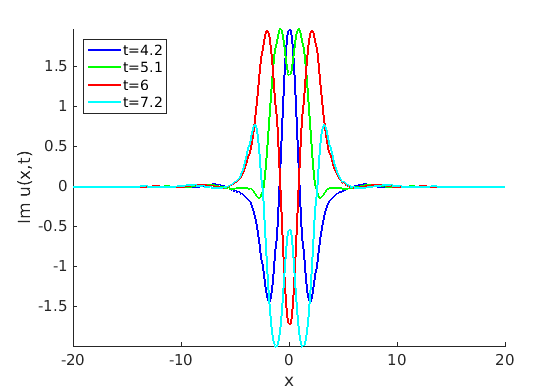
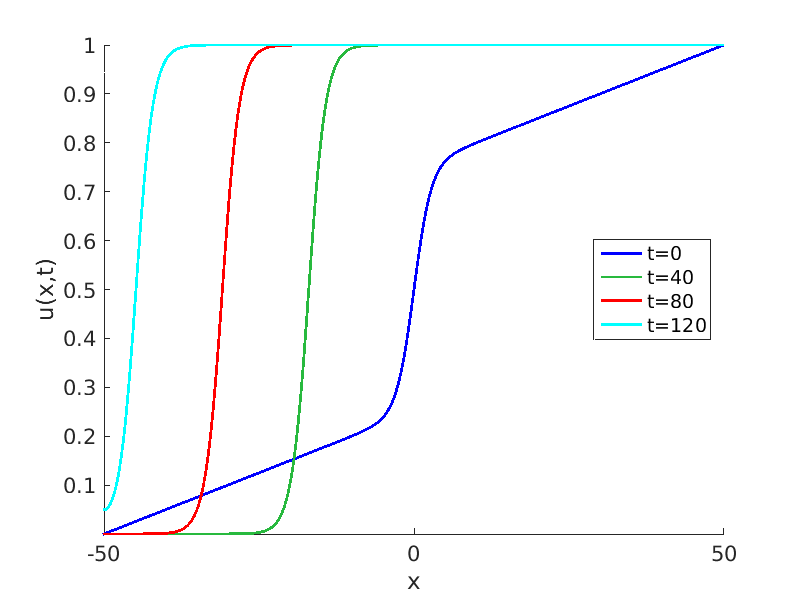
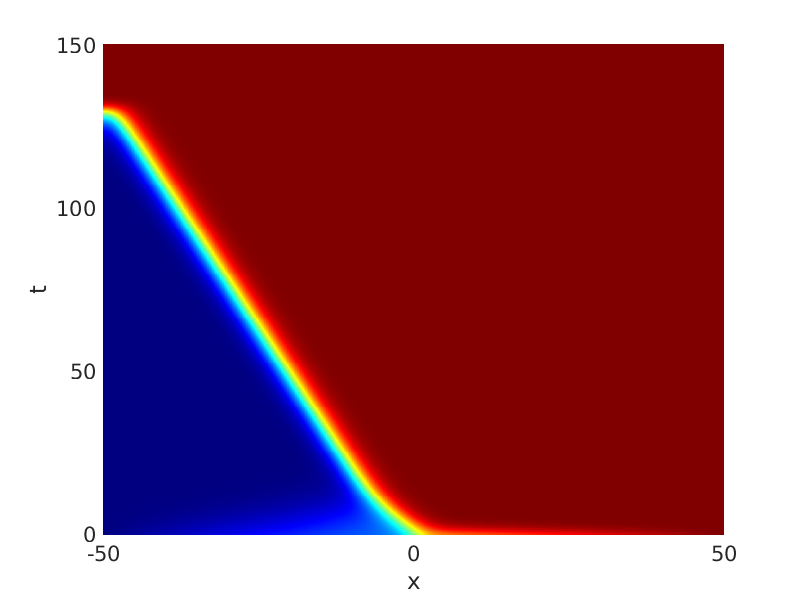
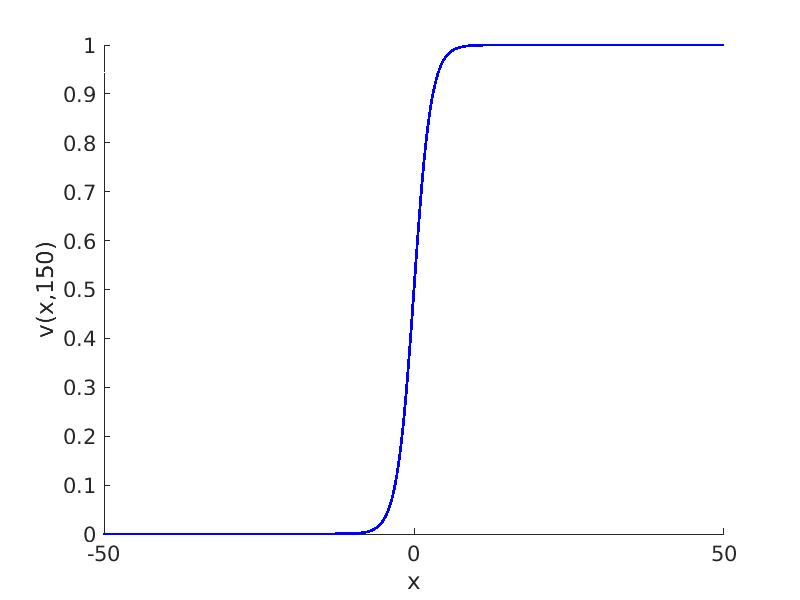
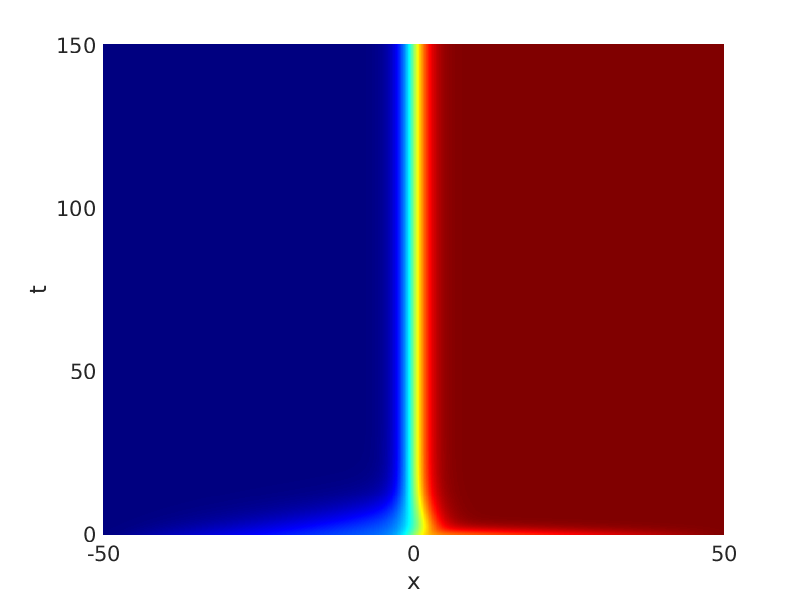
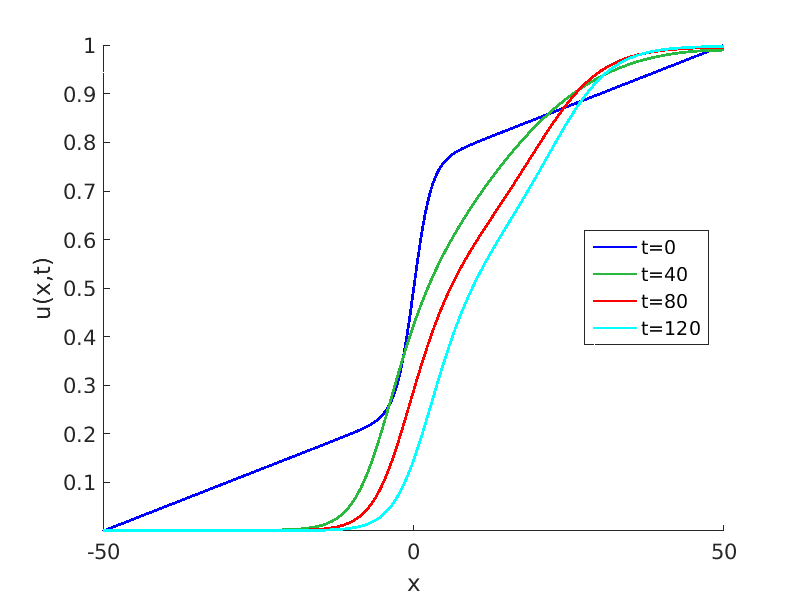
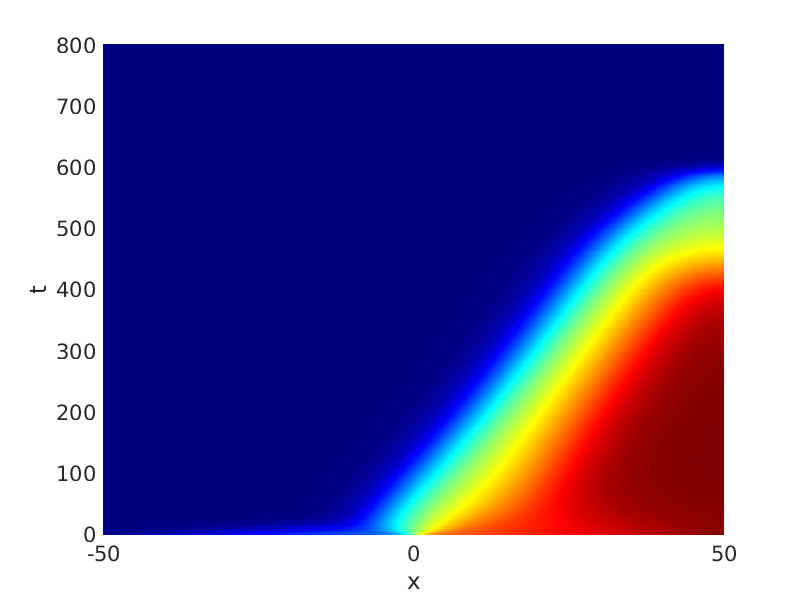
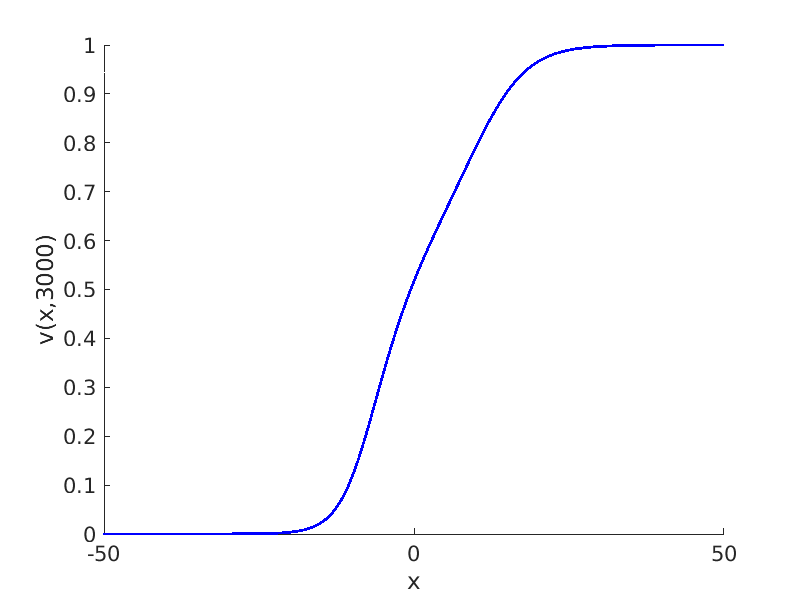
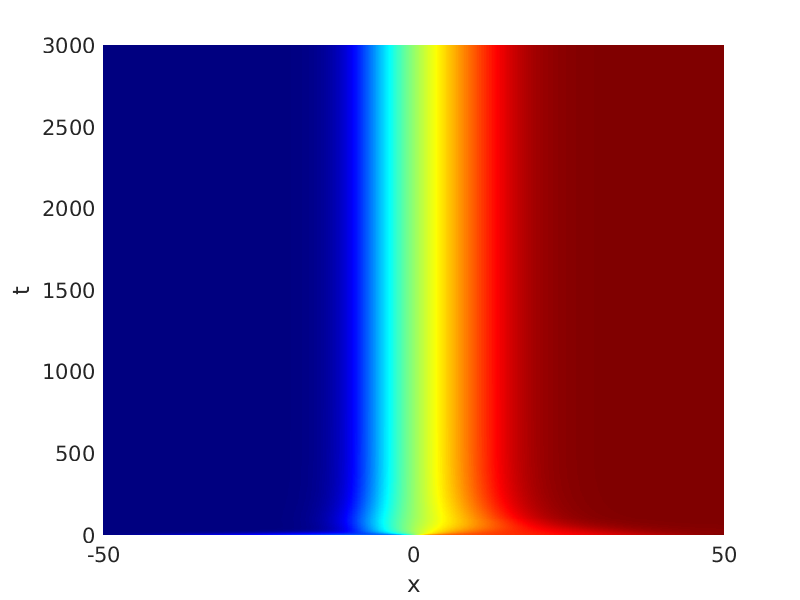
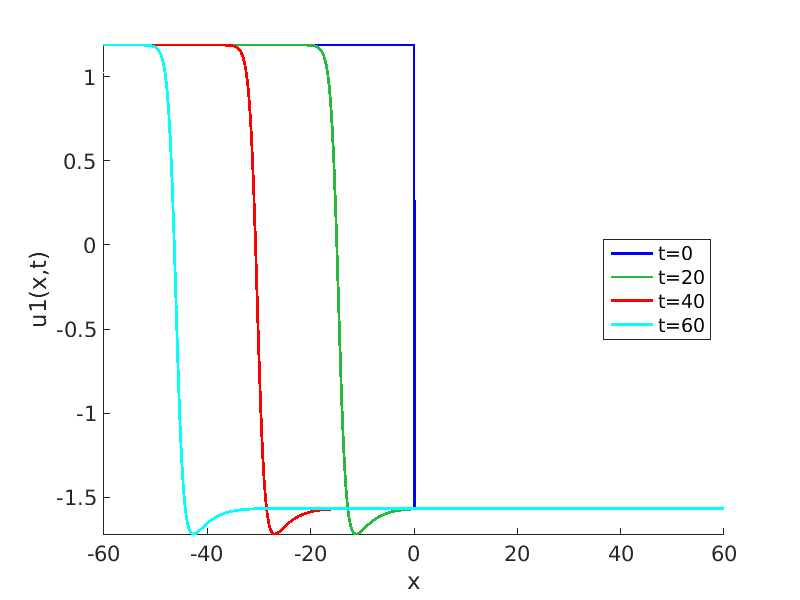
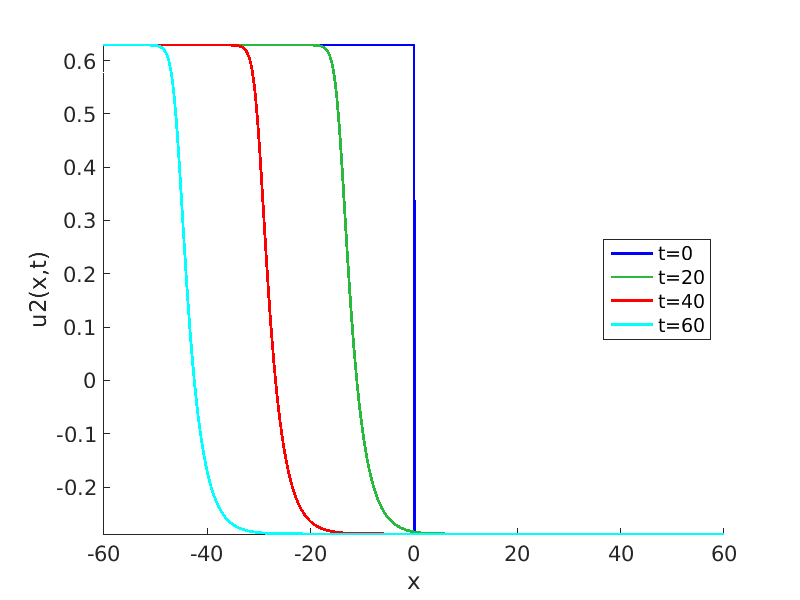
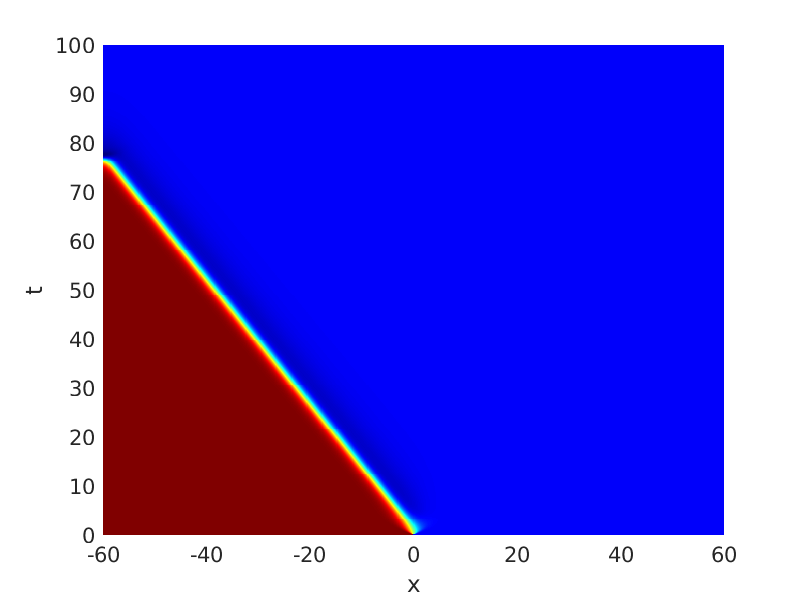
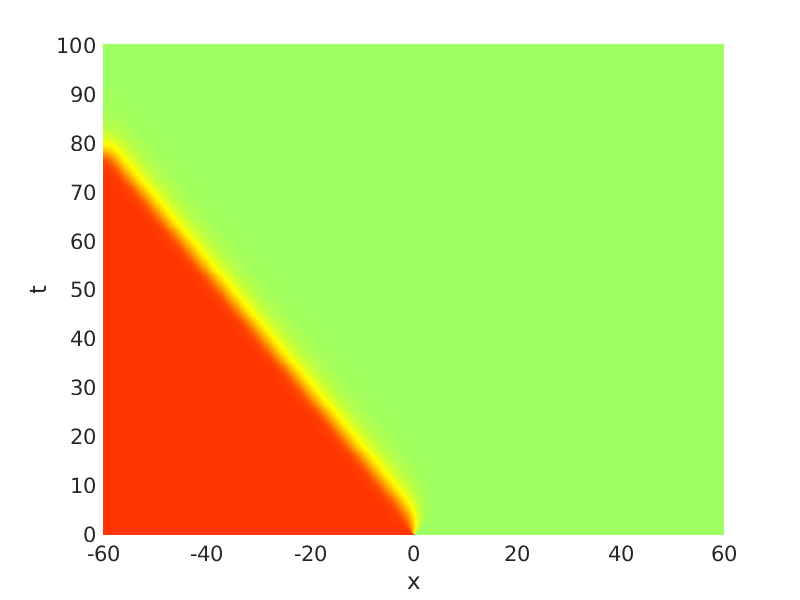
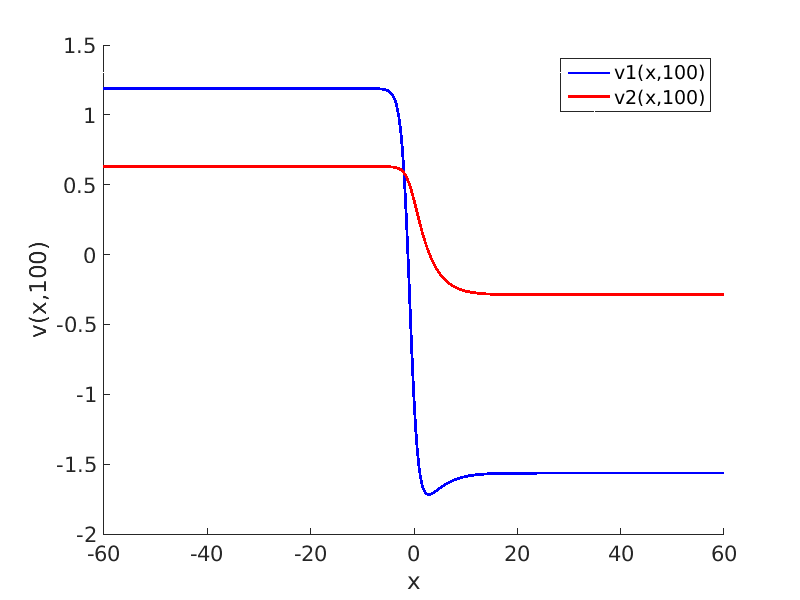
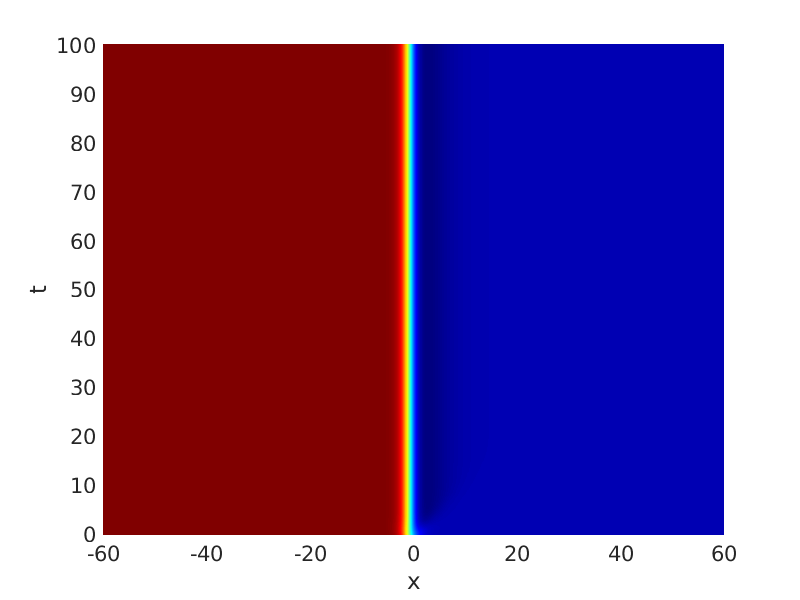
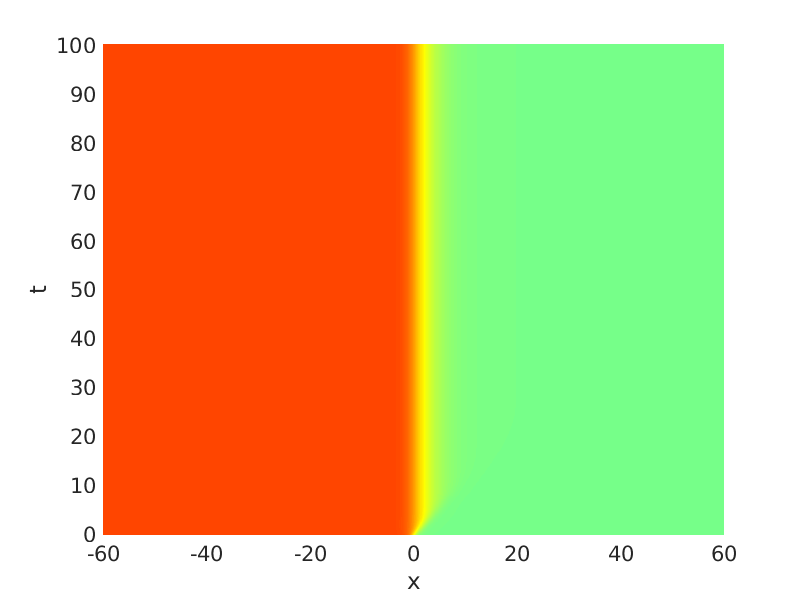
Freezing Relative Equilibria in Equivariant First-Order Evolution Equations (with Comsol Multiphysics 5.2)1.1 Traveling waves in reaction diffusion systems
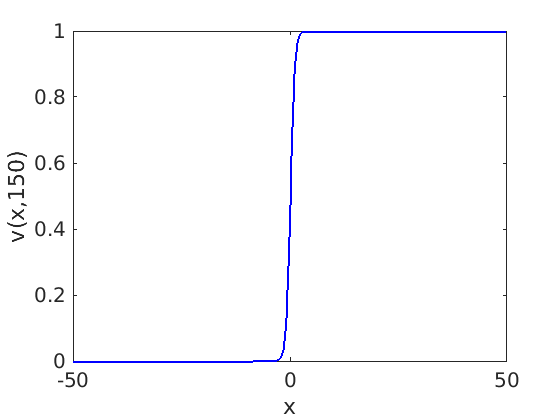
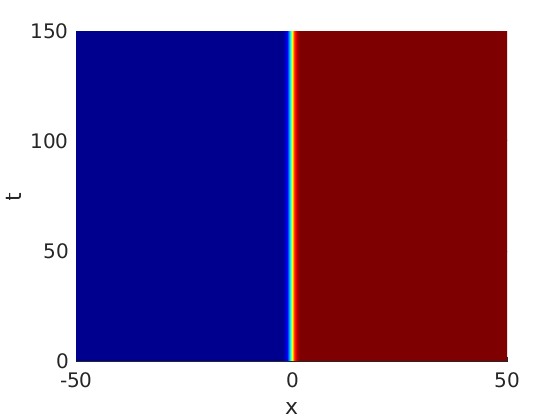
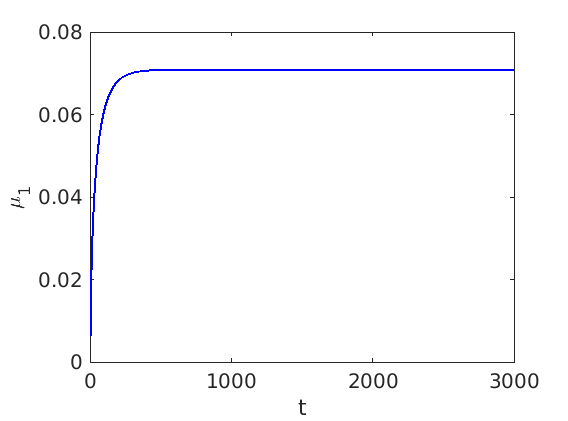
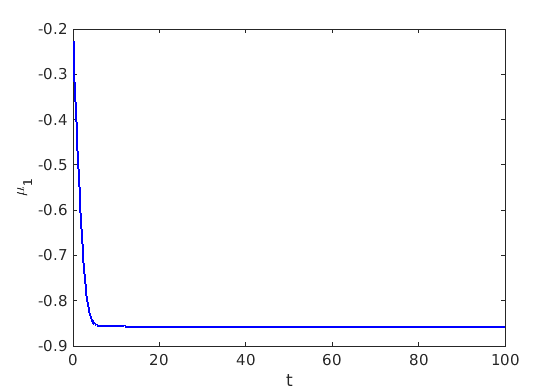
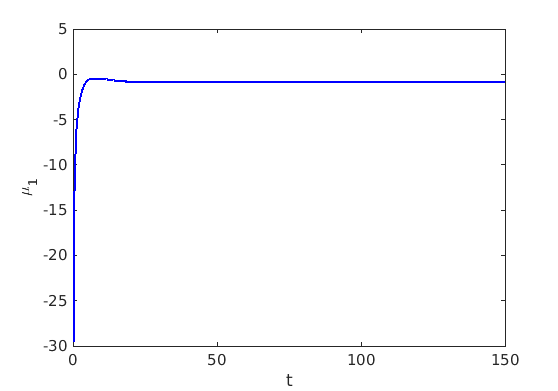
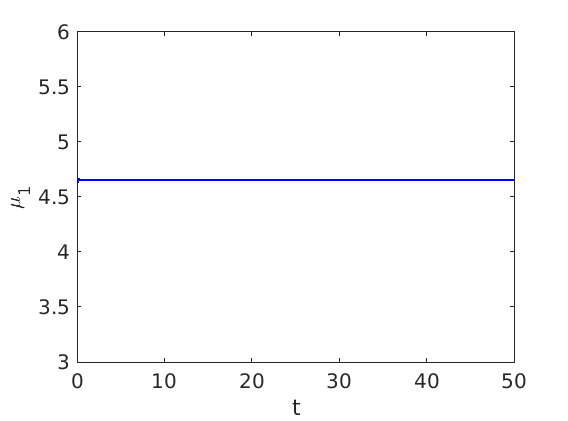
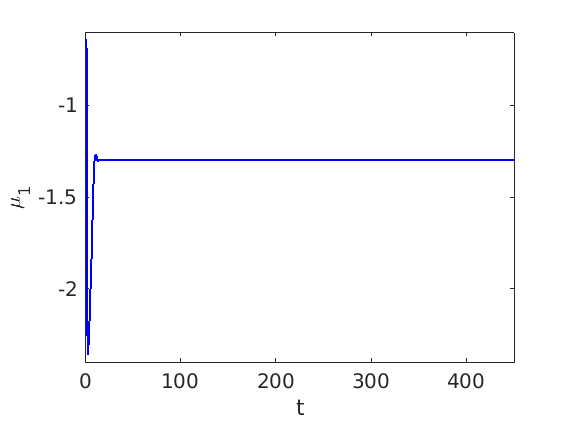
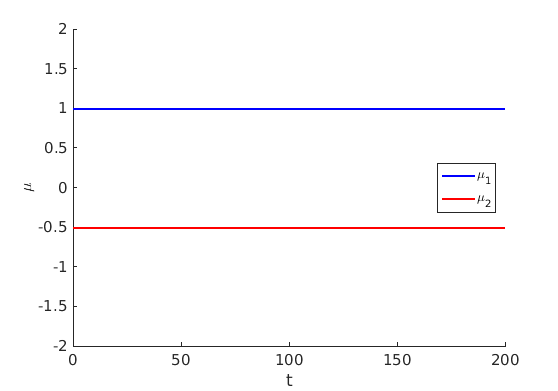
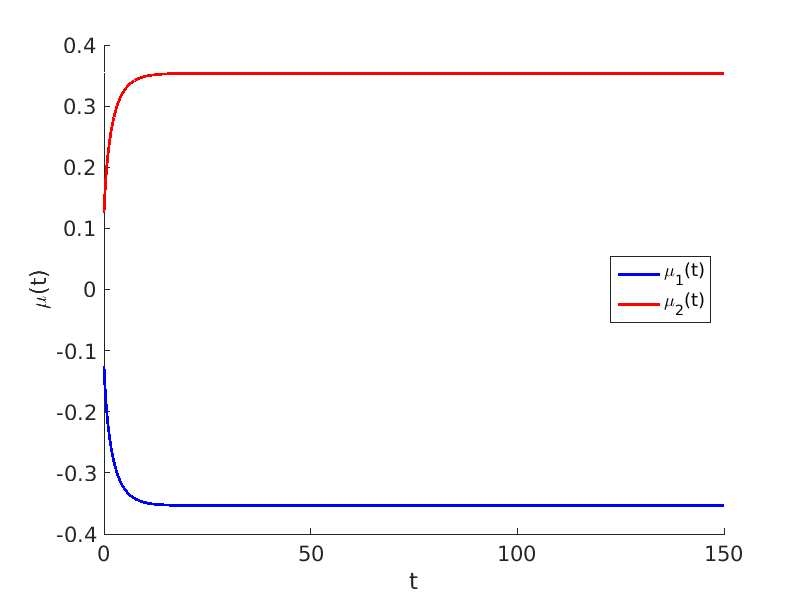
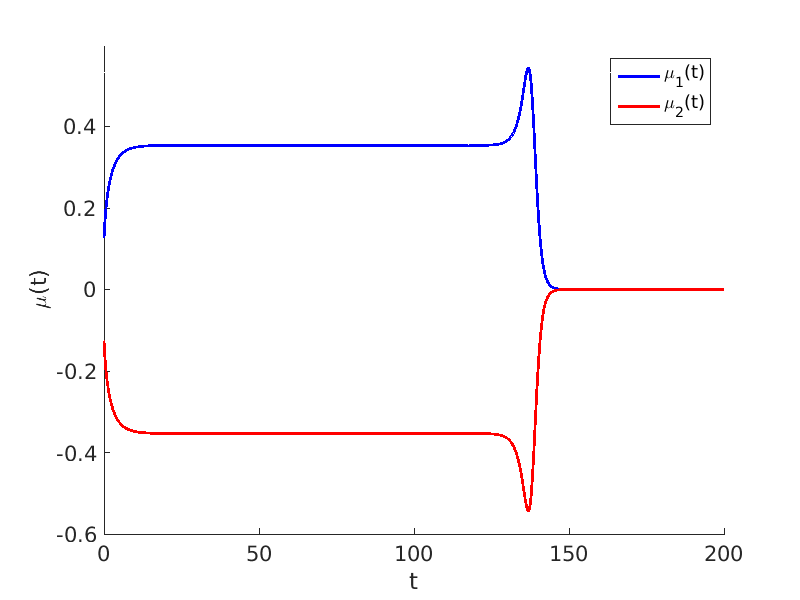
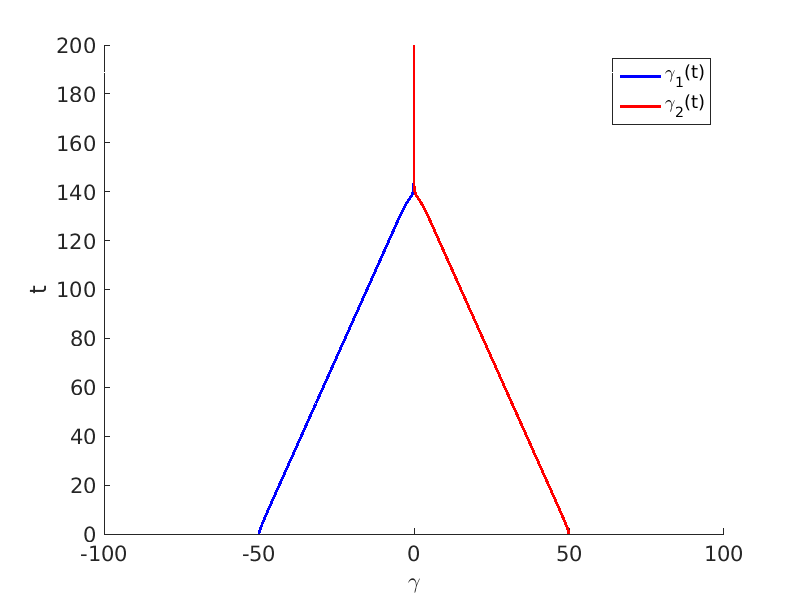
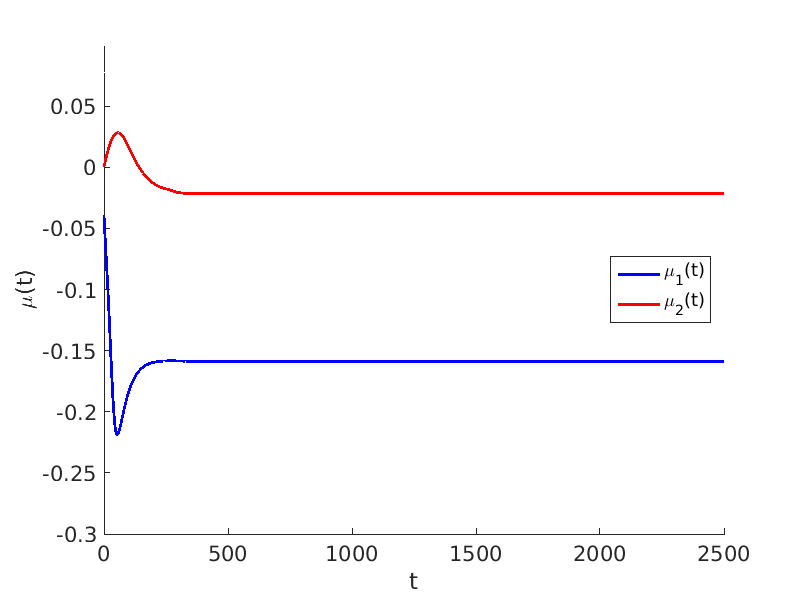
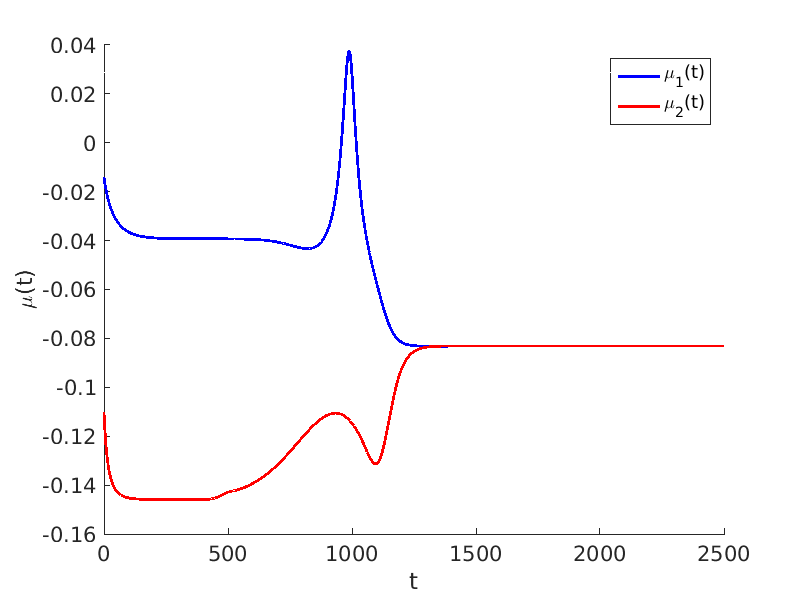
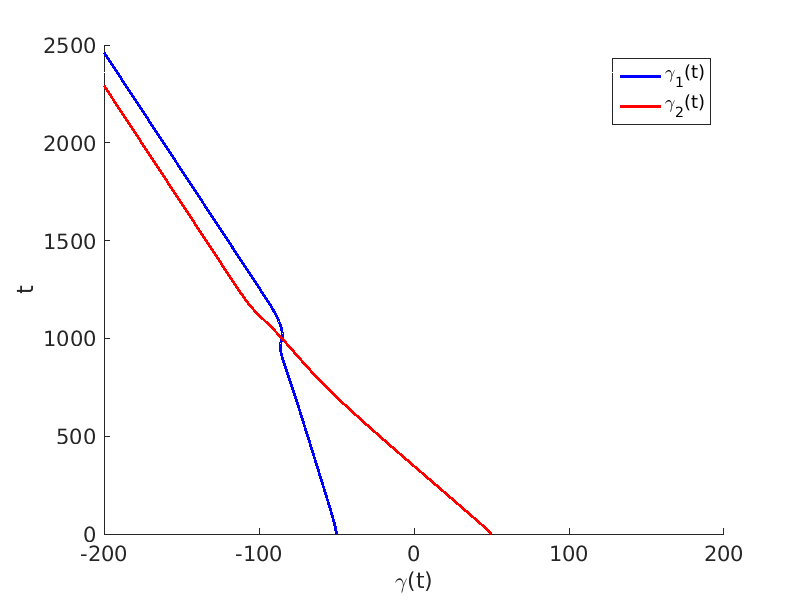
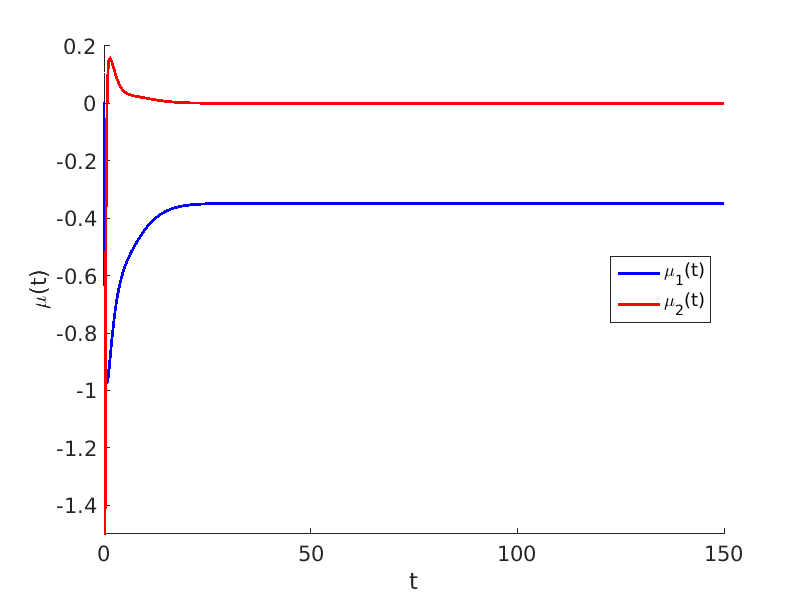
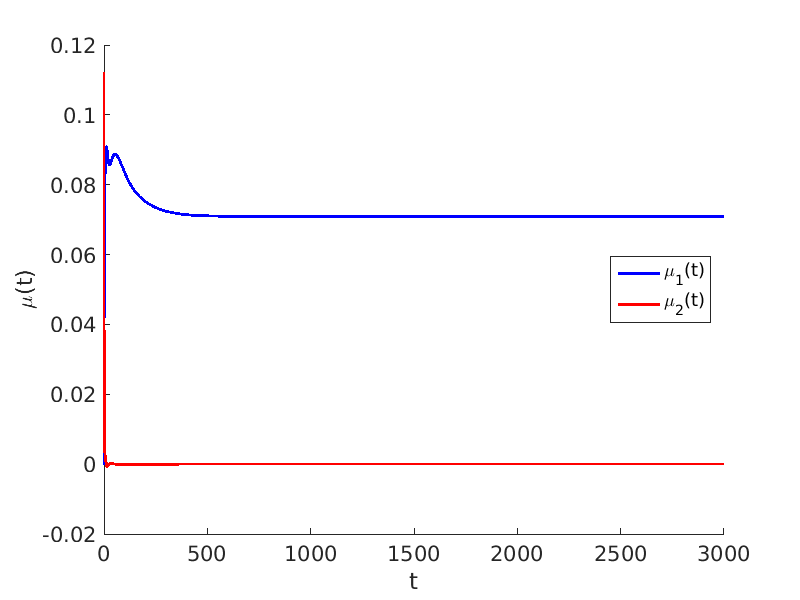
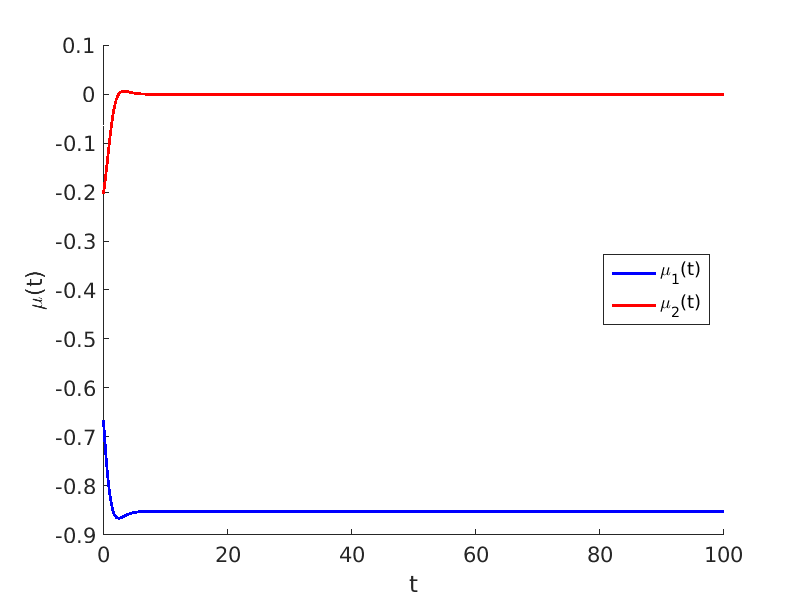
1.2 Freezing method for traveling waves
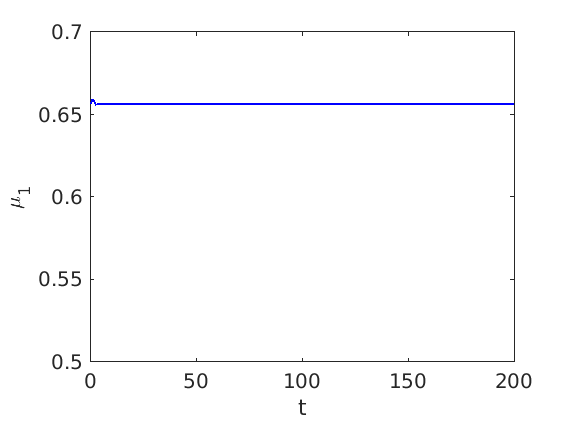
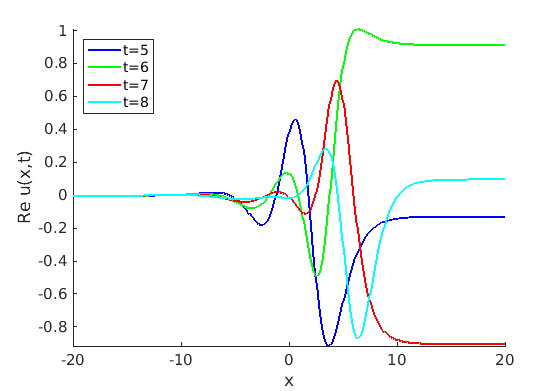
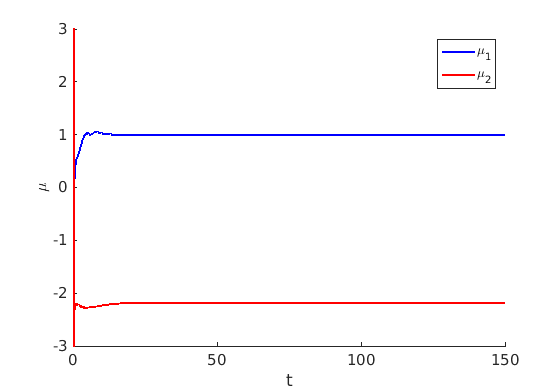
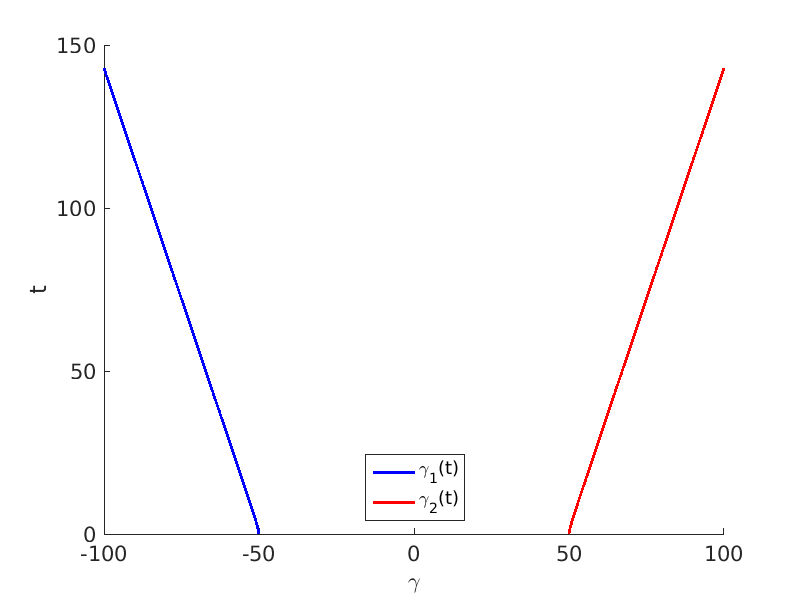
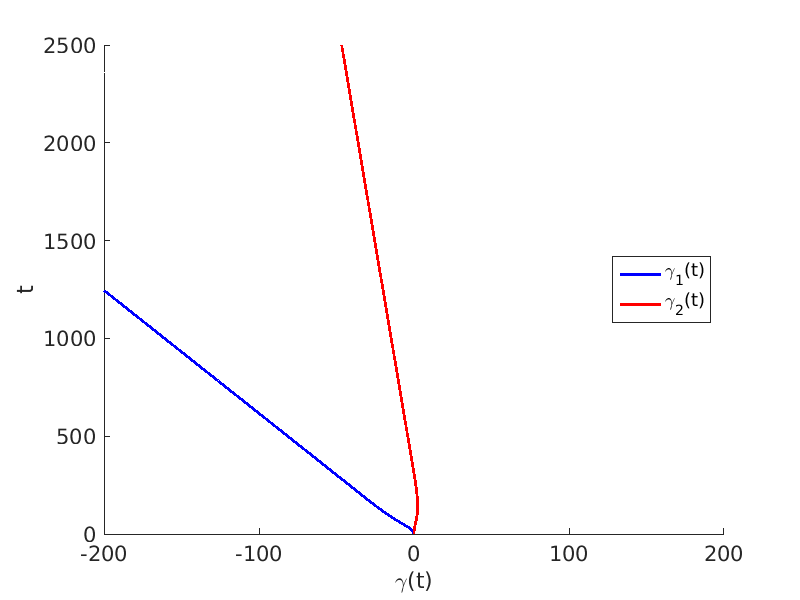
1.3 Numerical approximation of traveling waves via freezing method
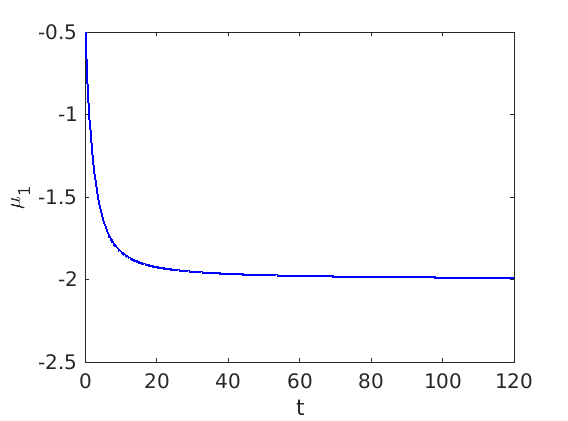
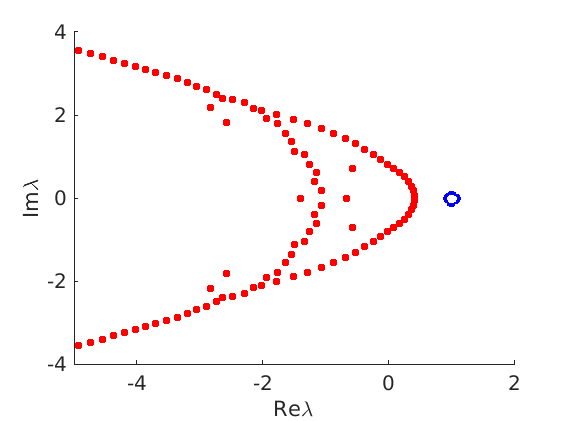
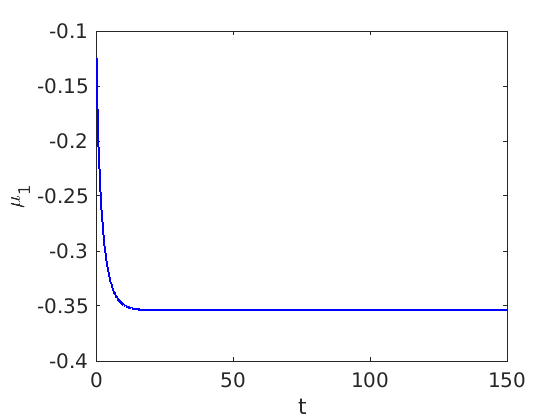
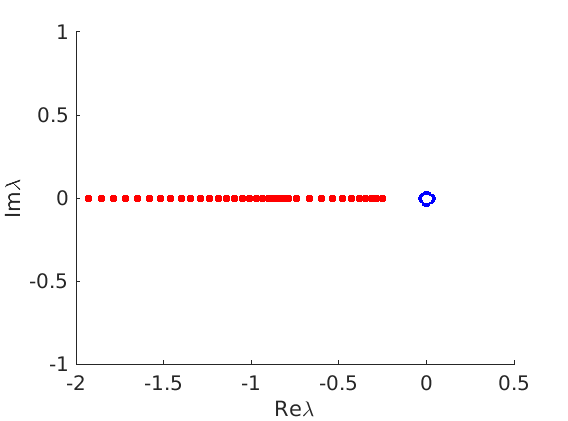
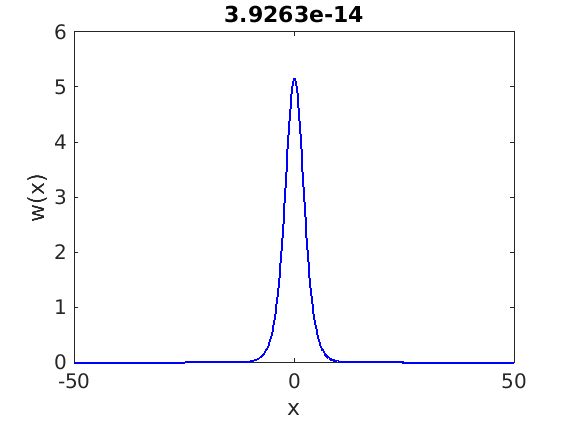
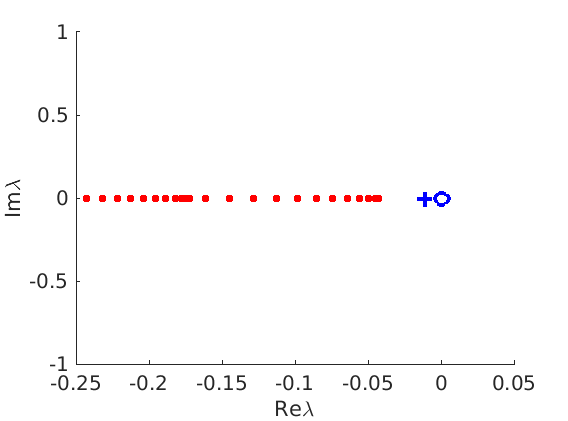
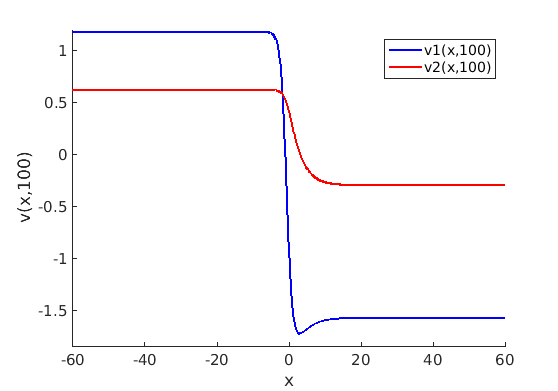
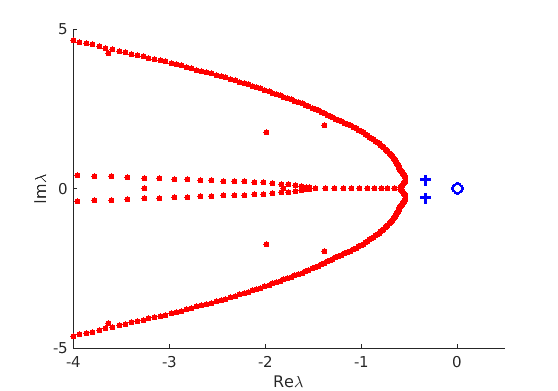
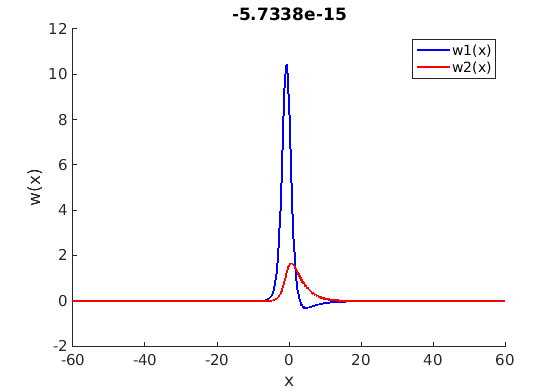
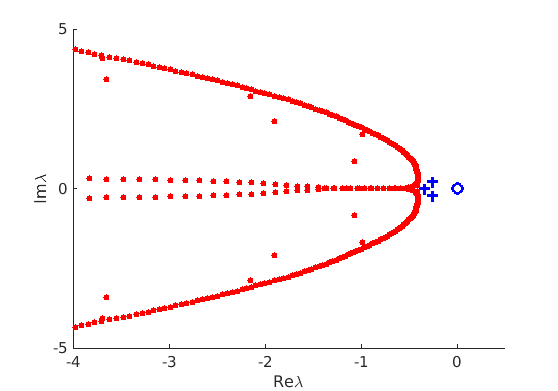
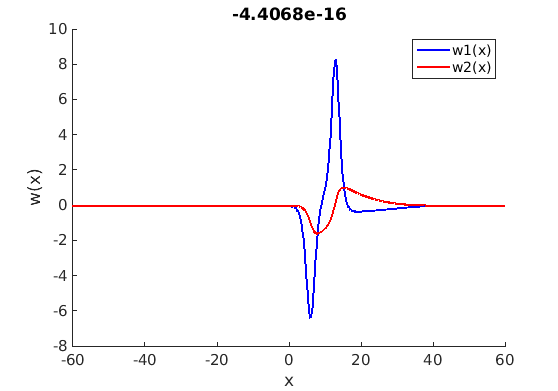
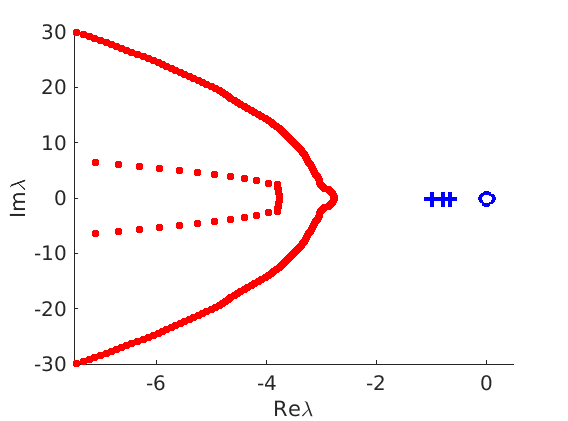
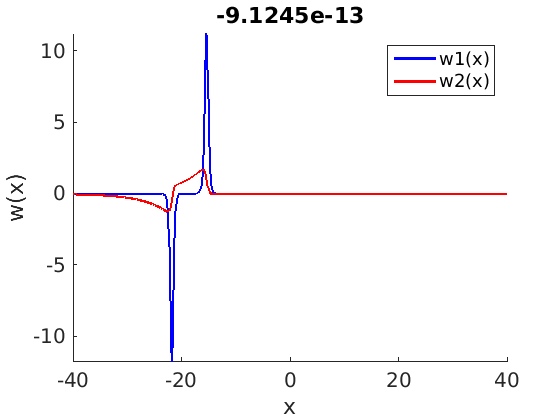
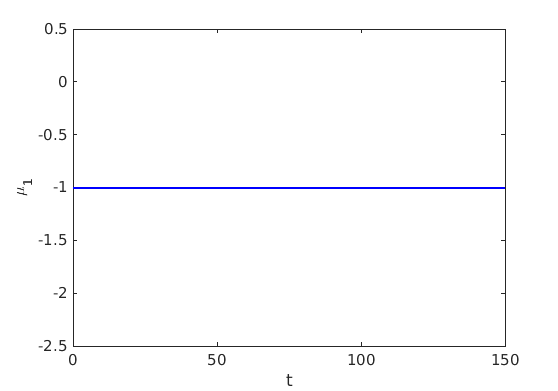
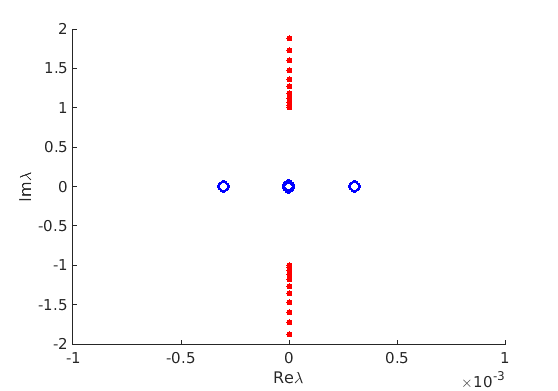
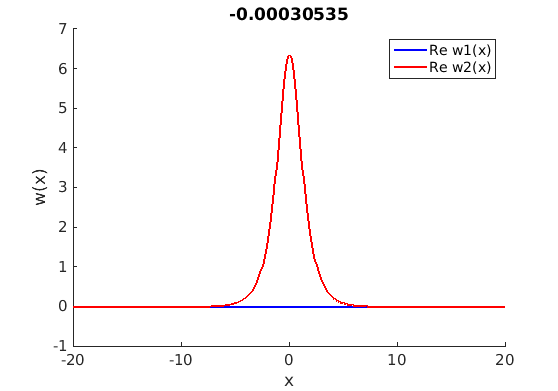
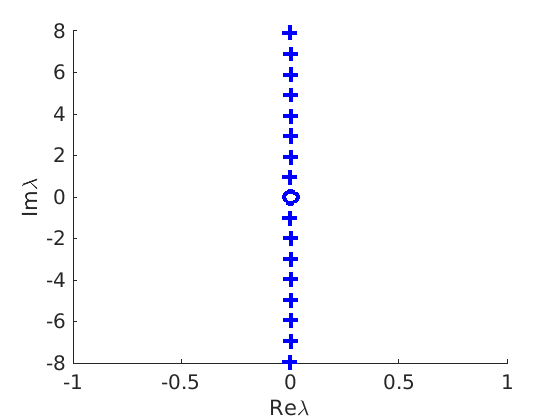
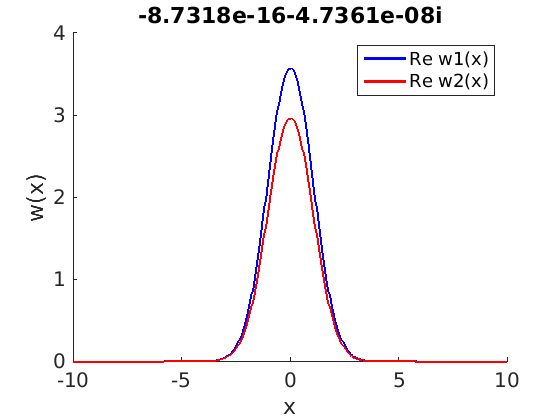
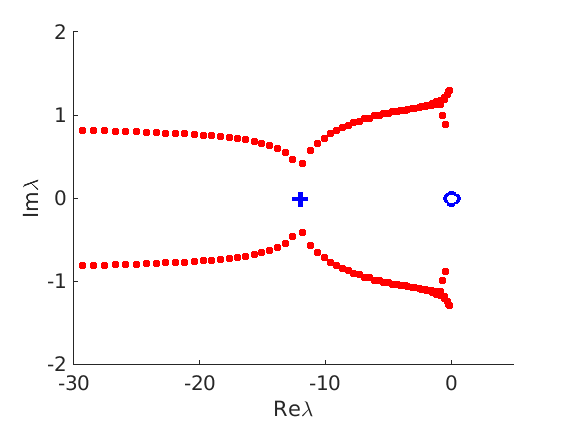
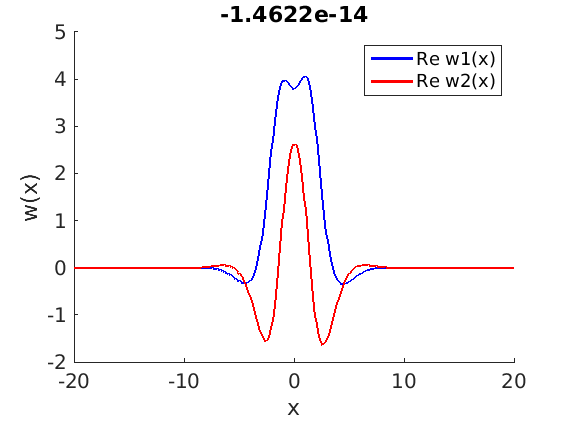
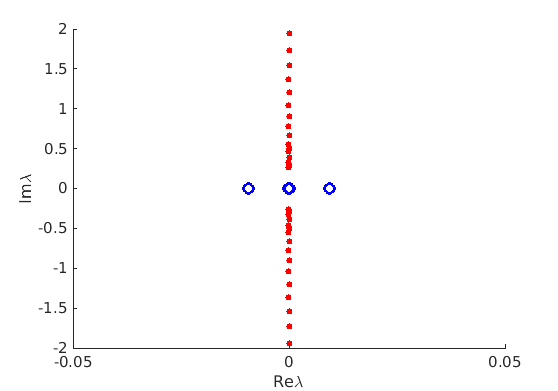
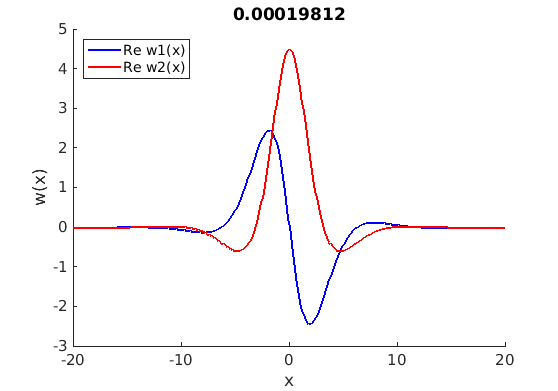
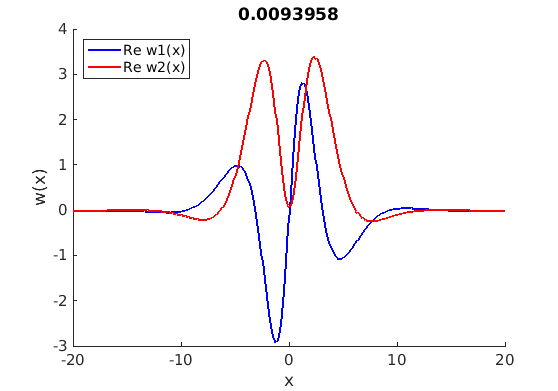
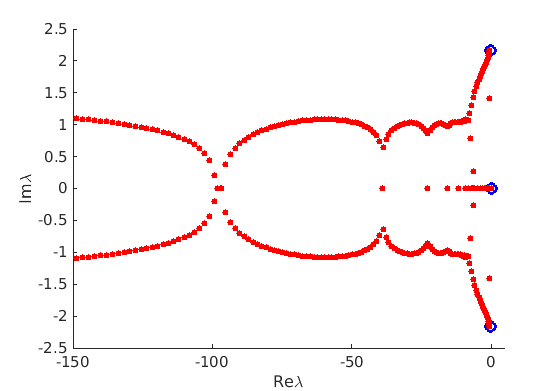
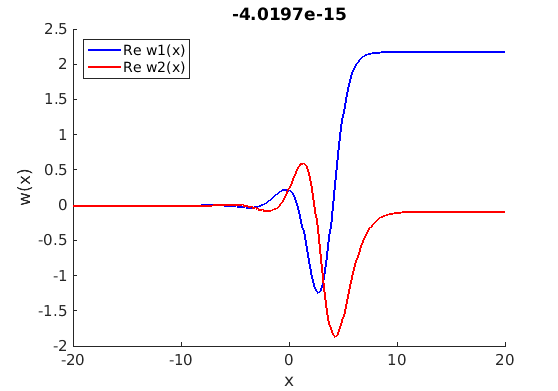
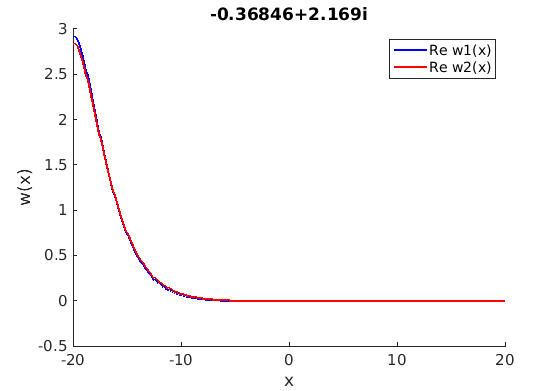
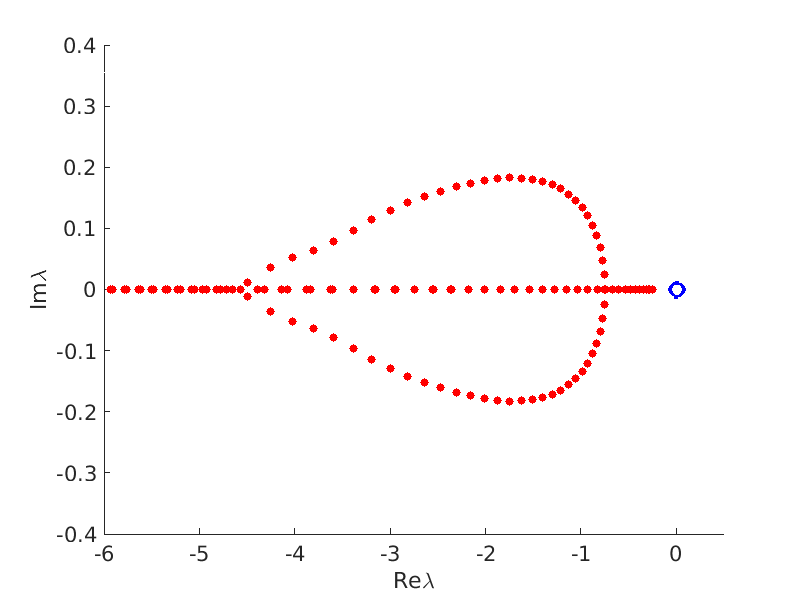
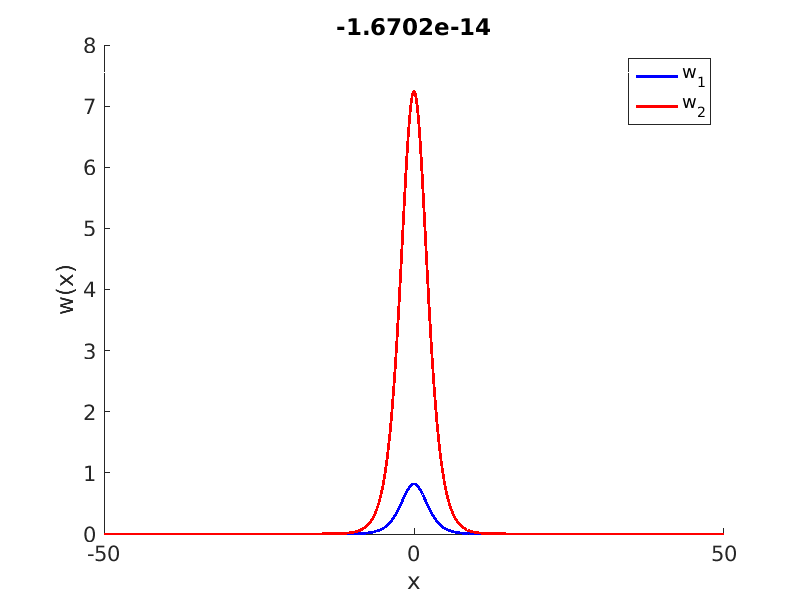
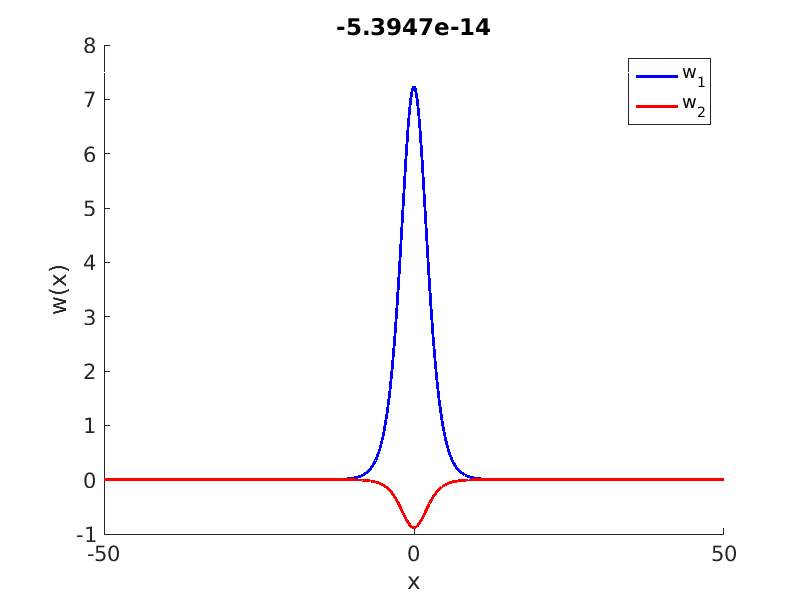
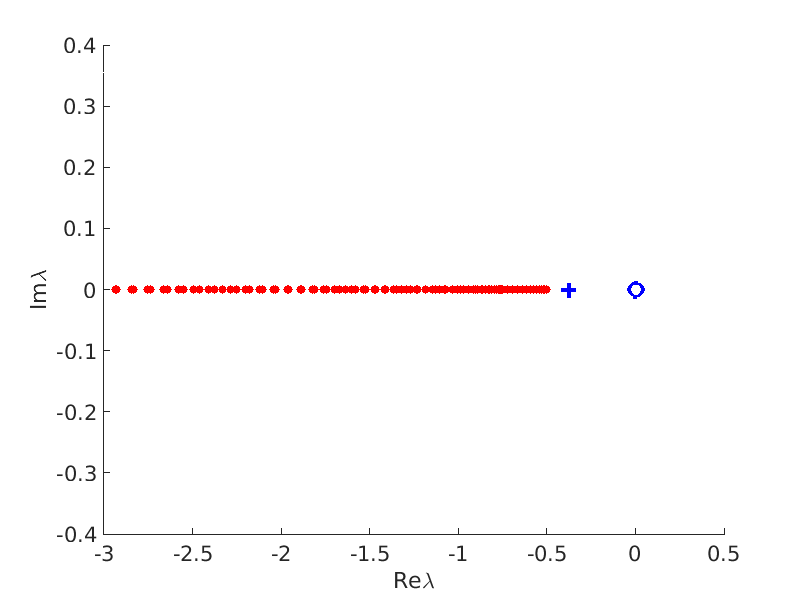
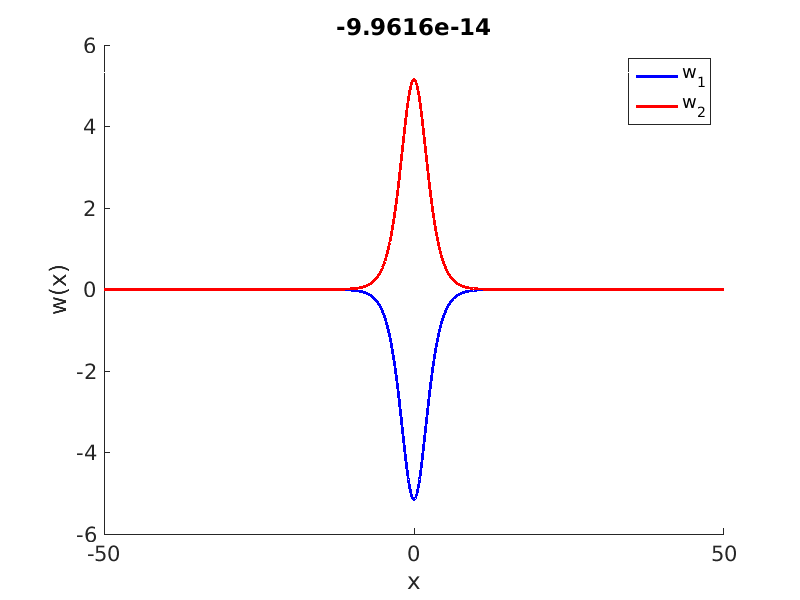
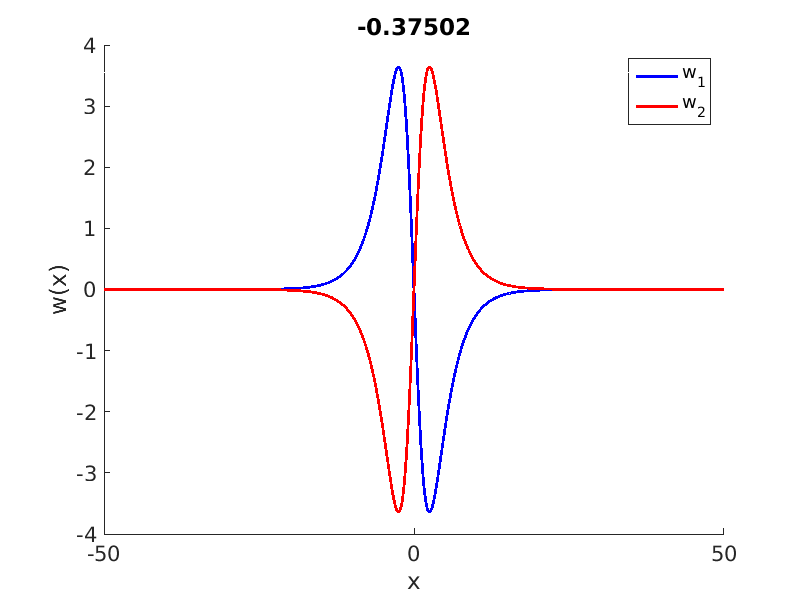
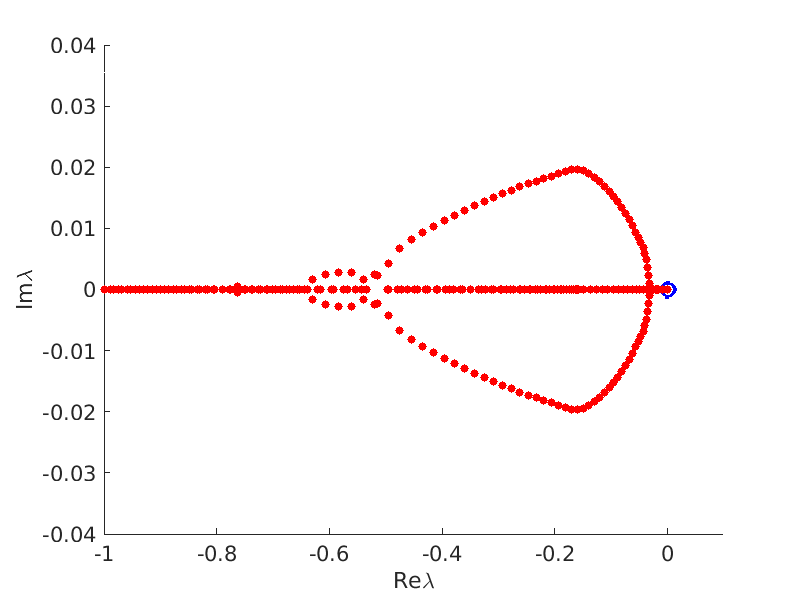
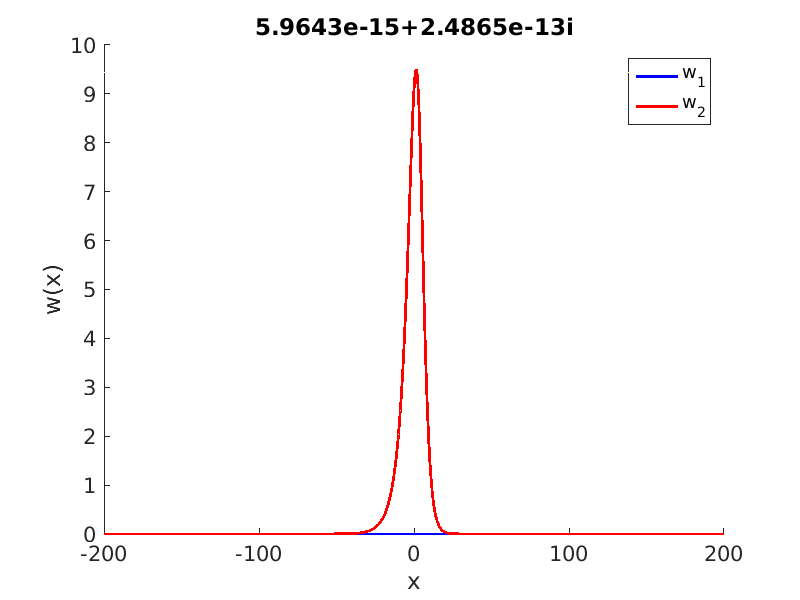
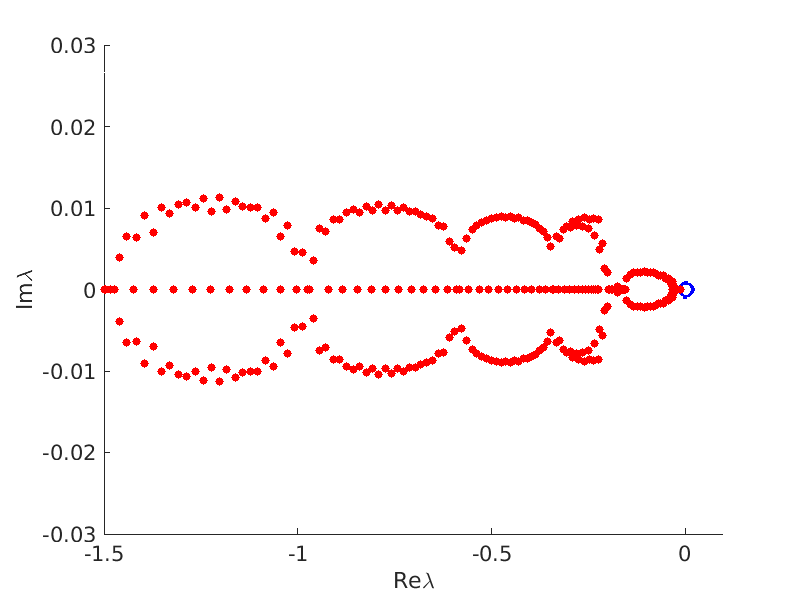
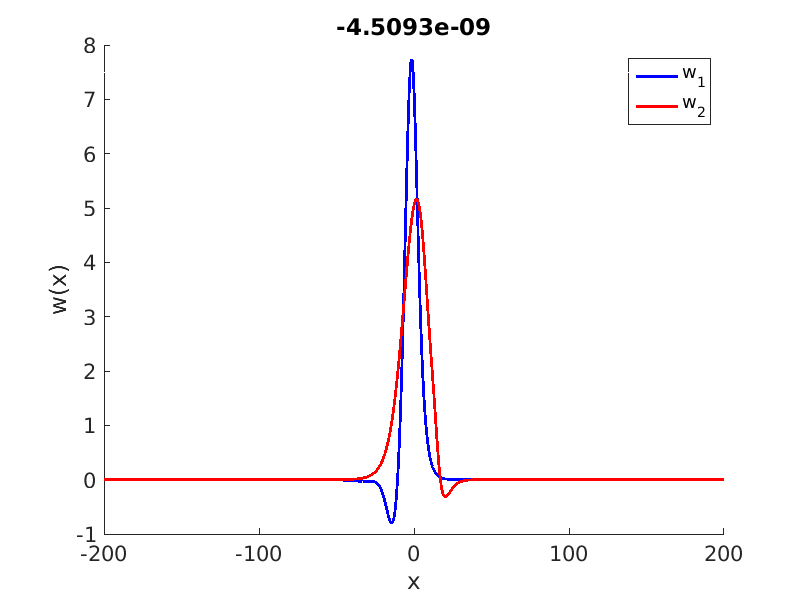
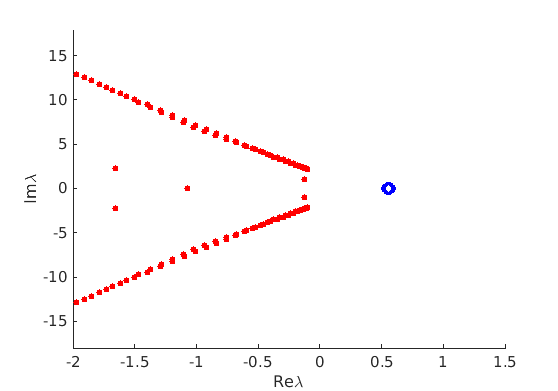
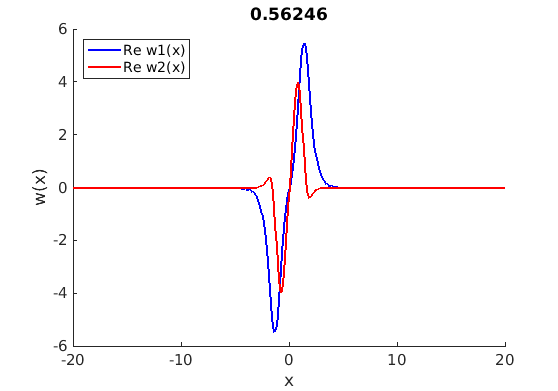
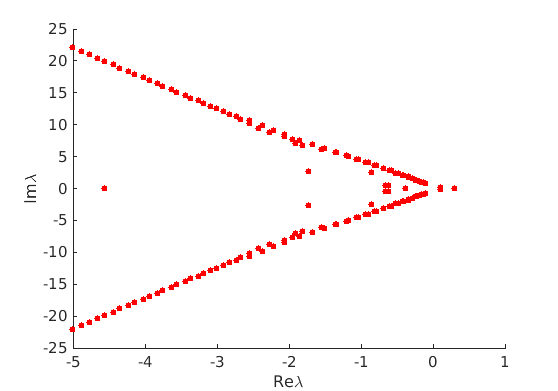
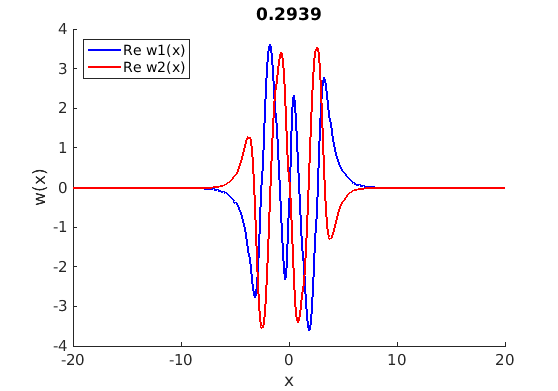
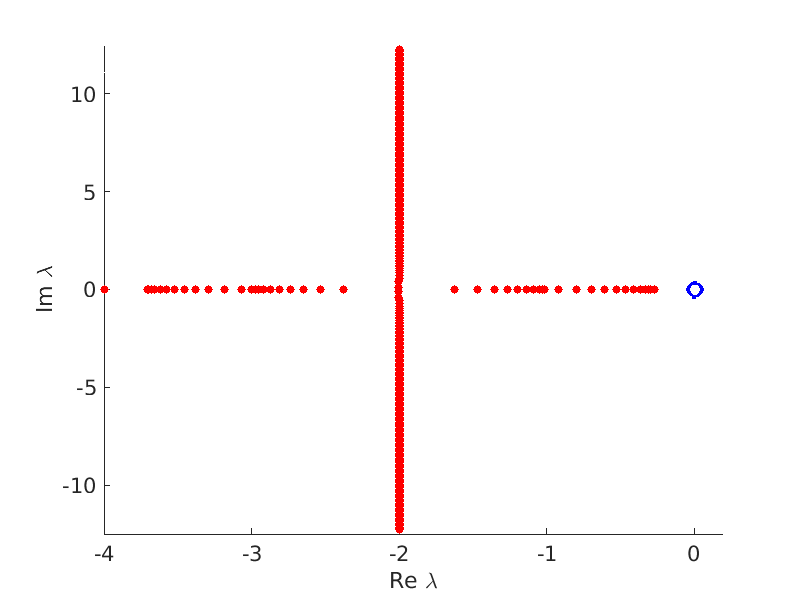
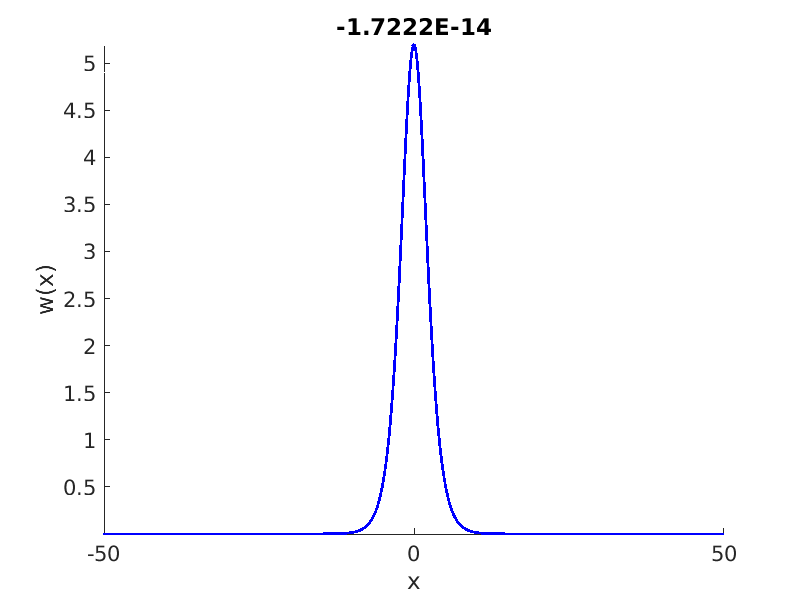
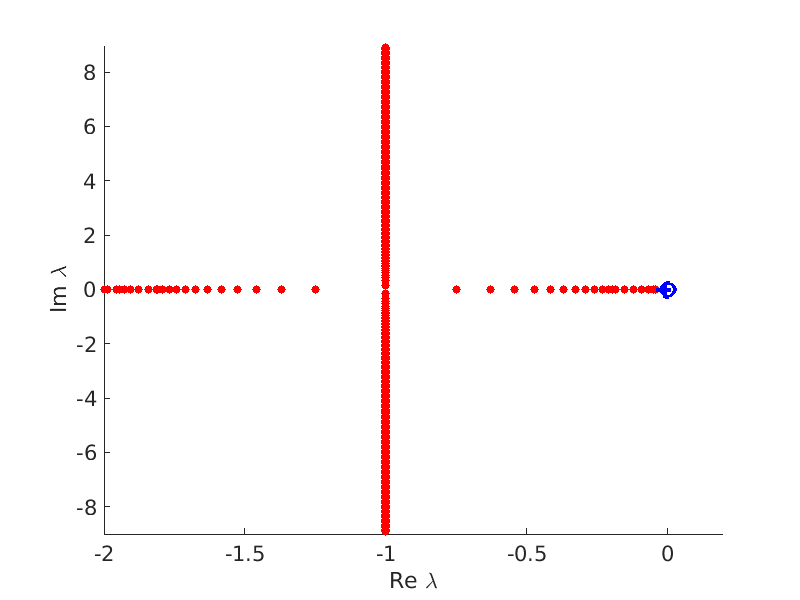
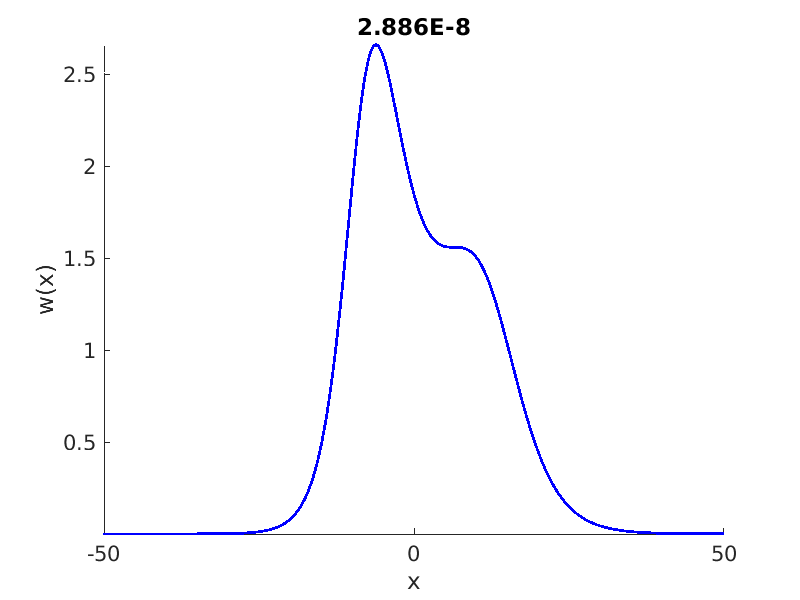
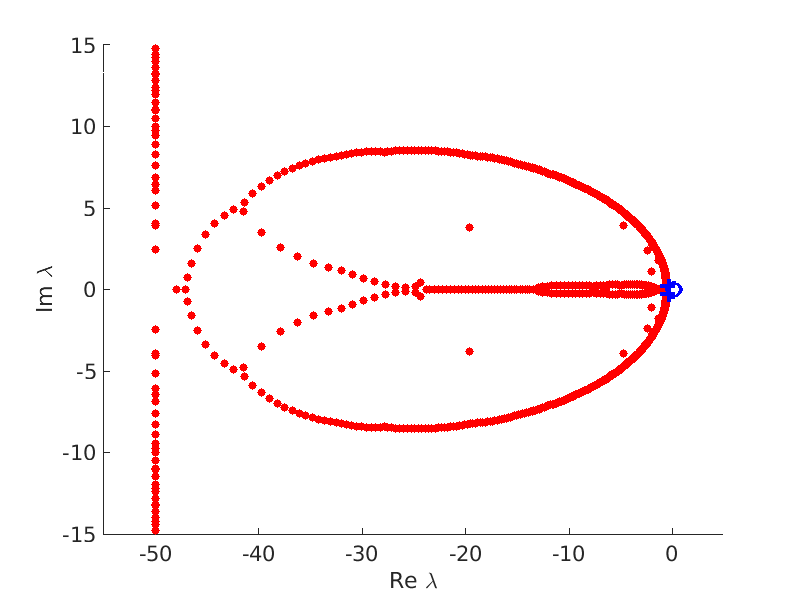
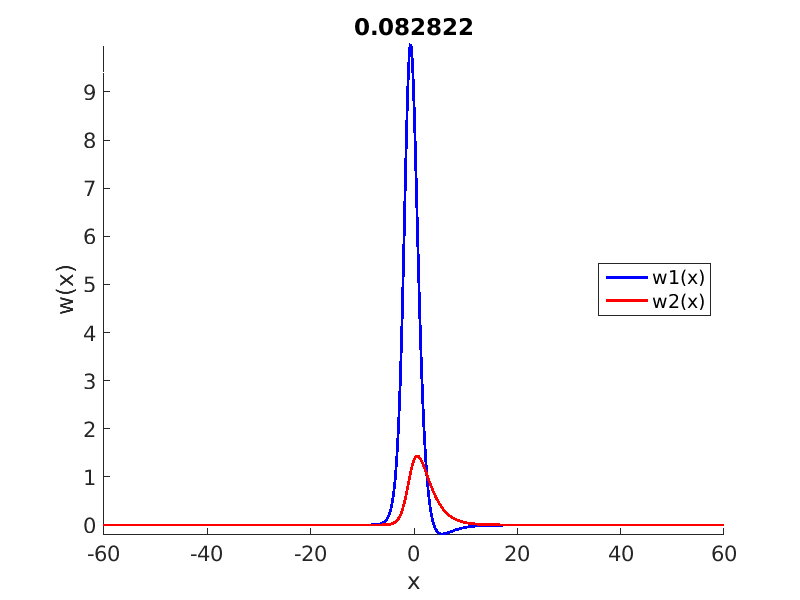
1.4 Spectra and eigenfunctions of traveling waves
1.4.1 Point spectrum of traveling waves on the imaginary axis
1.4.2 Essential spectrum of traveling waves
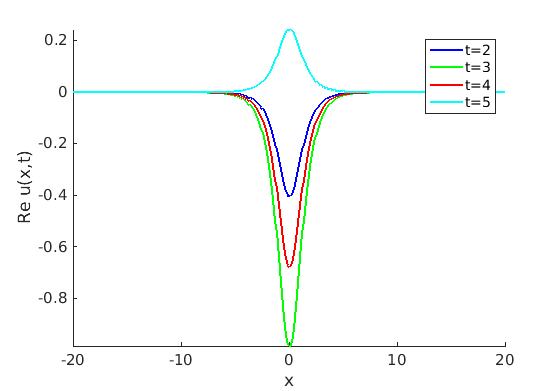
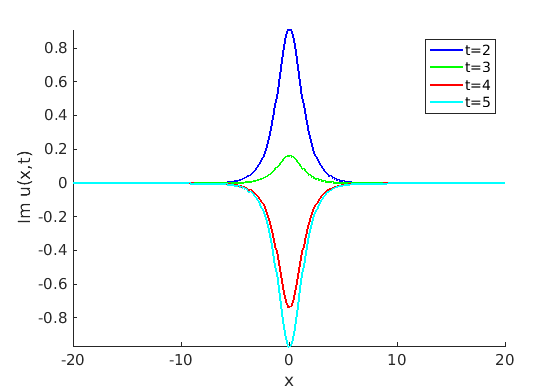
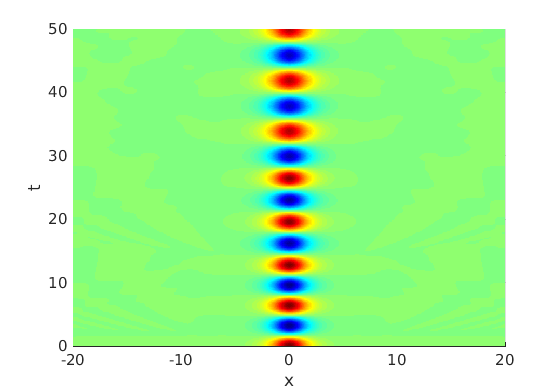
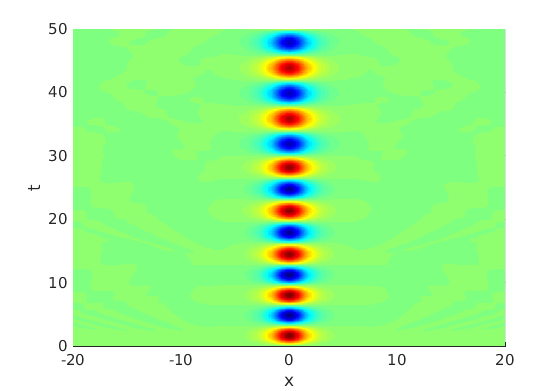
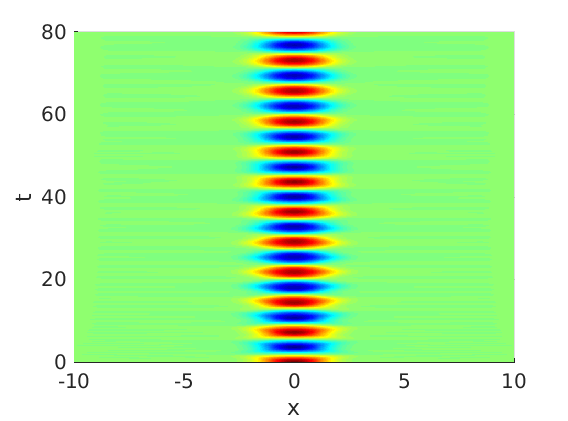
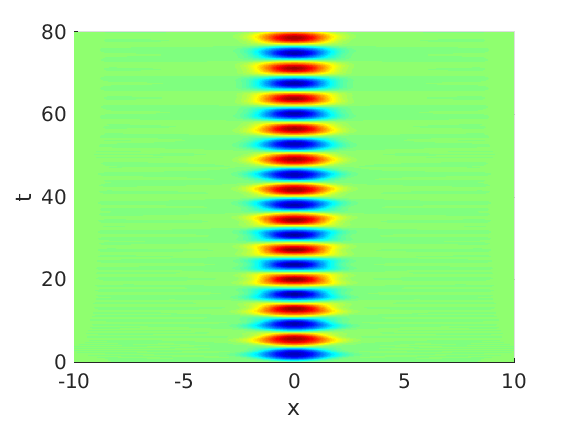
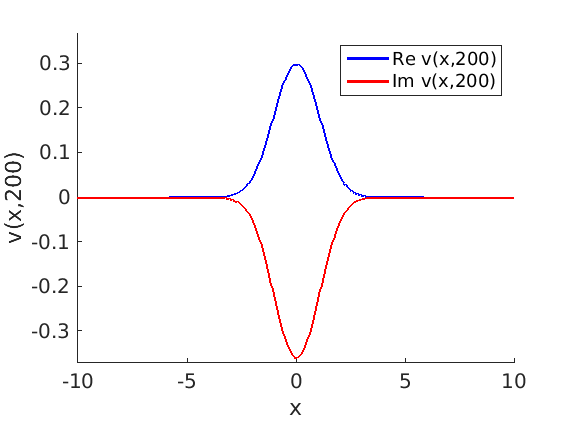
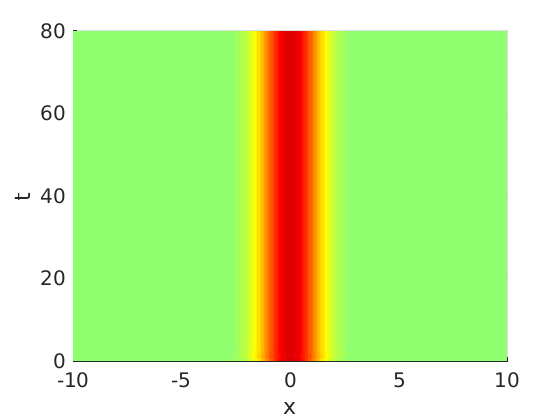
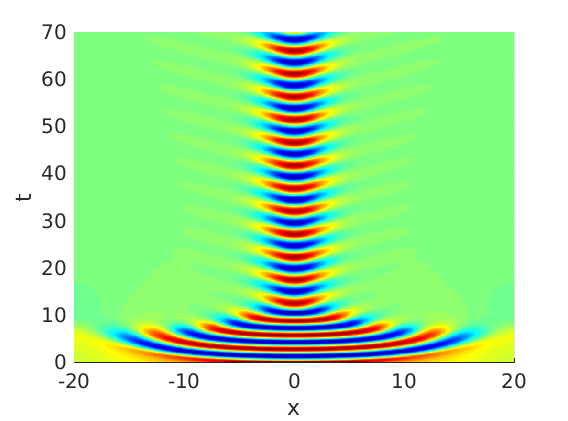
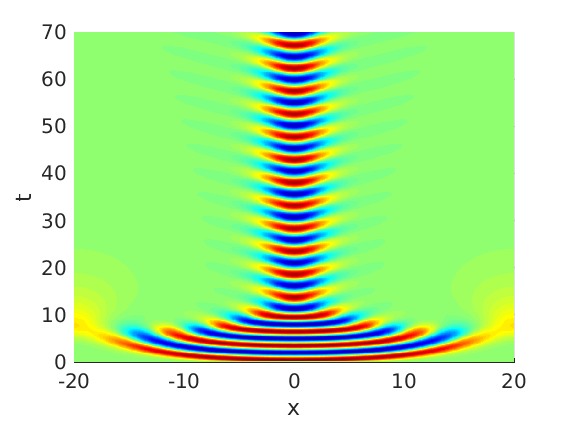
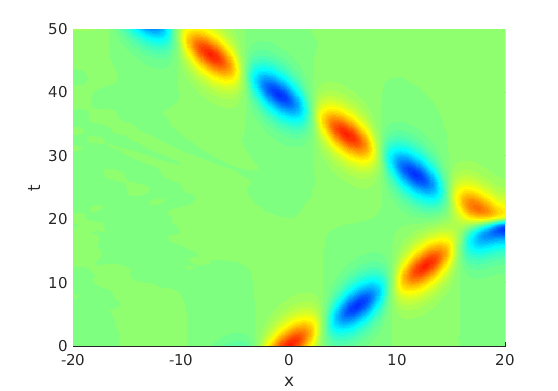
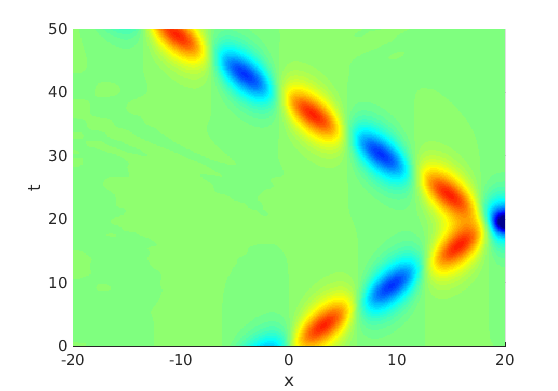
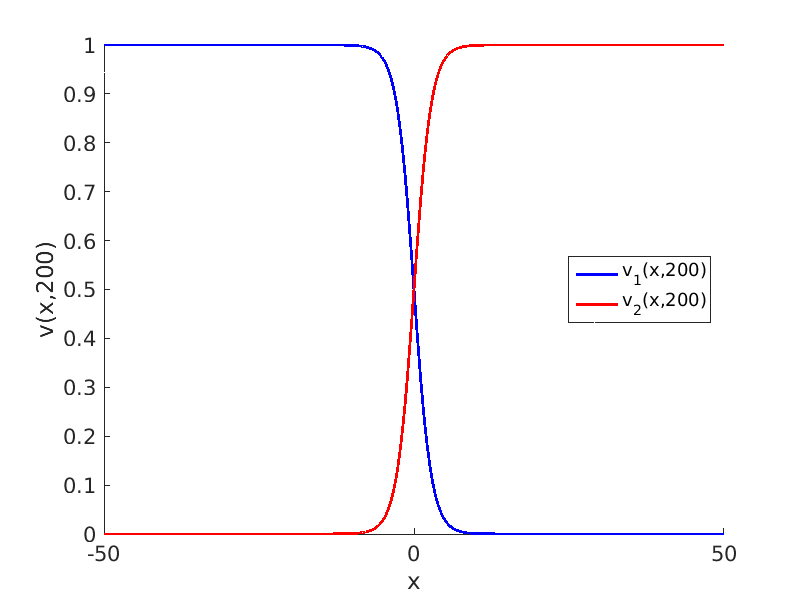
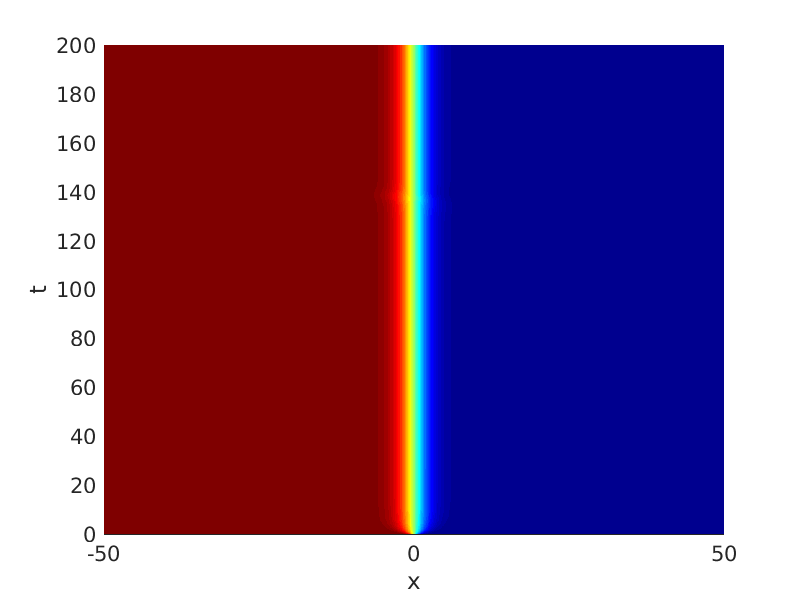
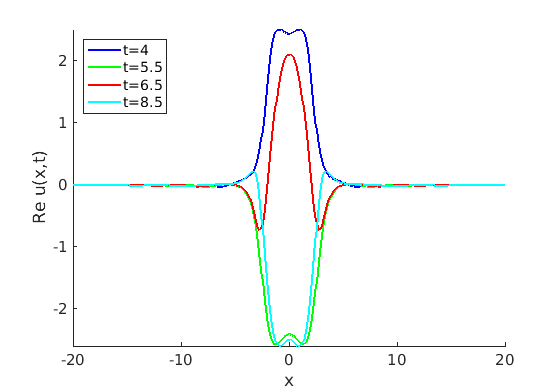
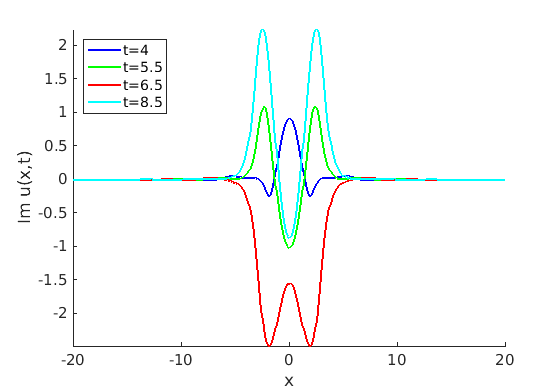
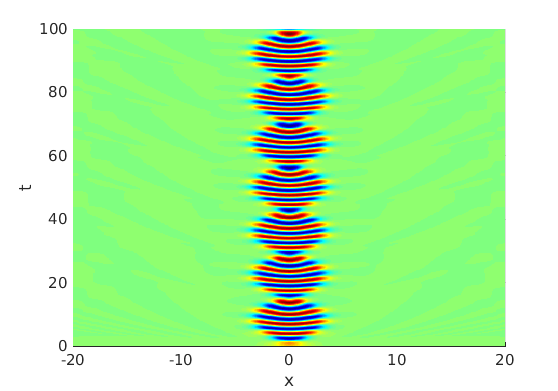
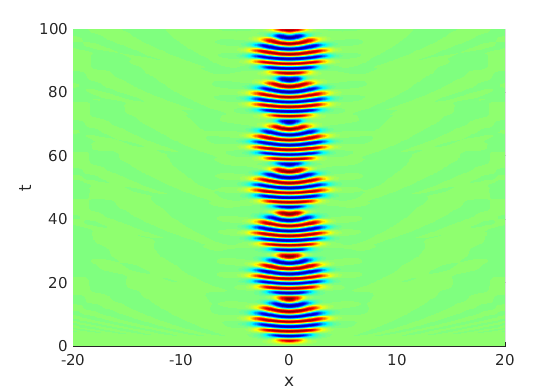
2.1 Oscillating waves in reaction diffusion systems
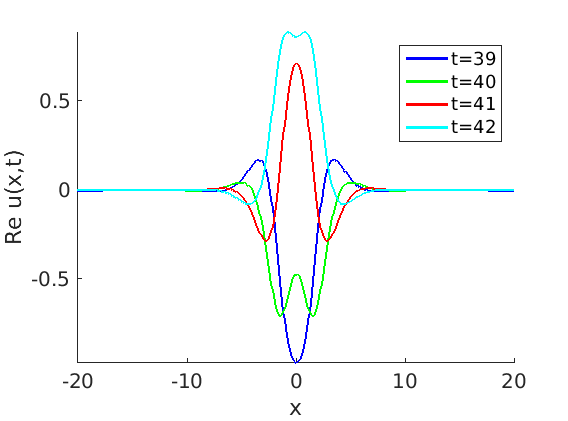
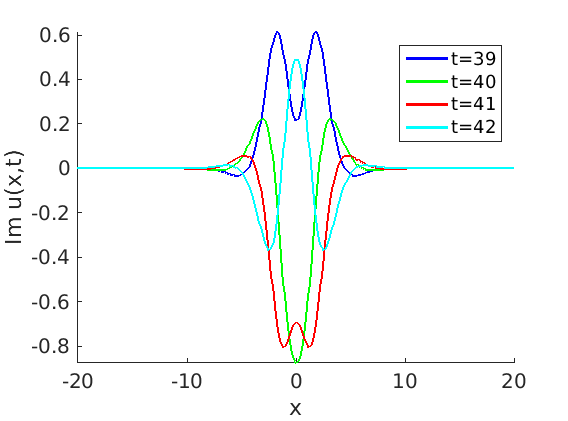
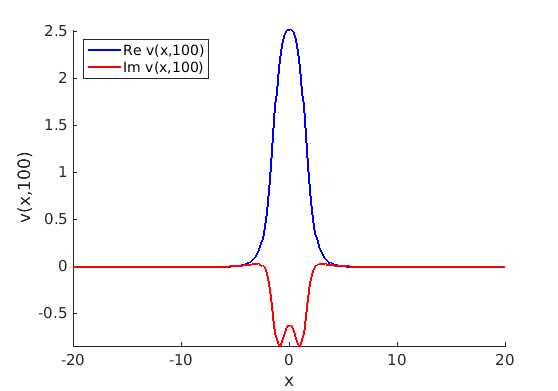
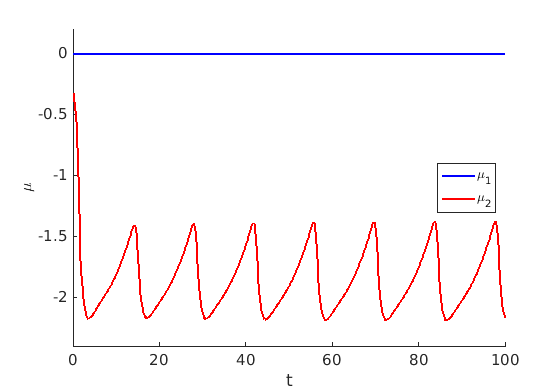
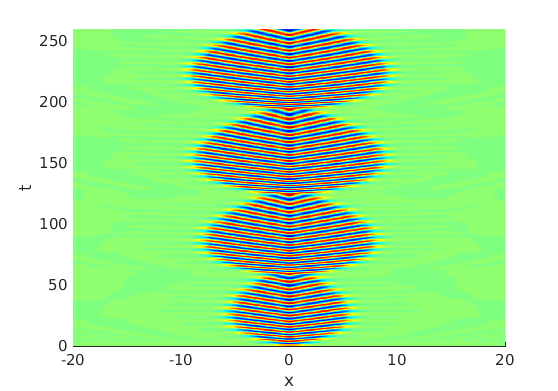
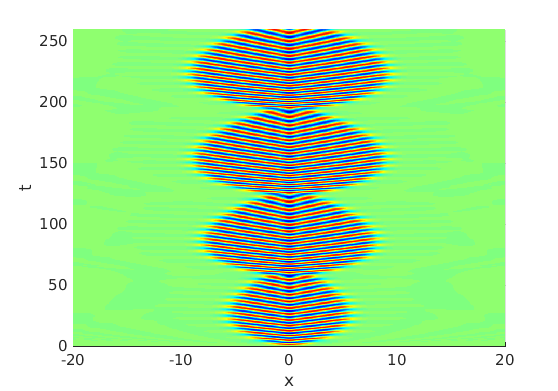
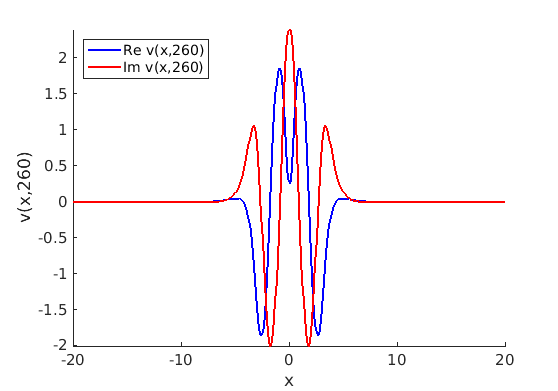
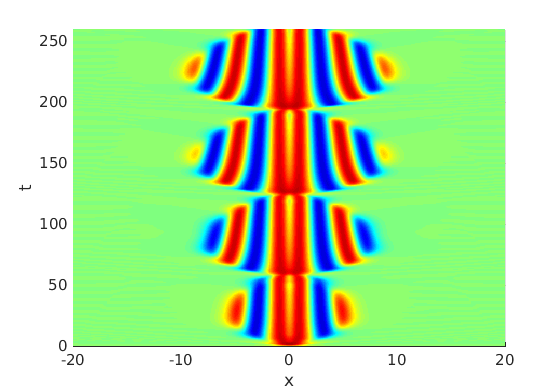
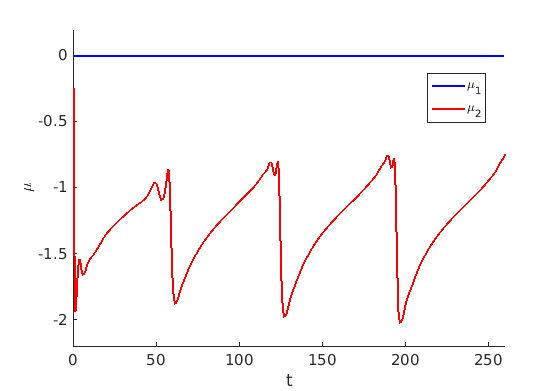
2.2 Freezing method for oscillating waves
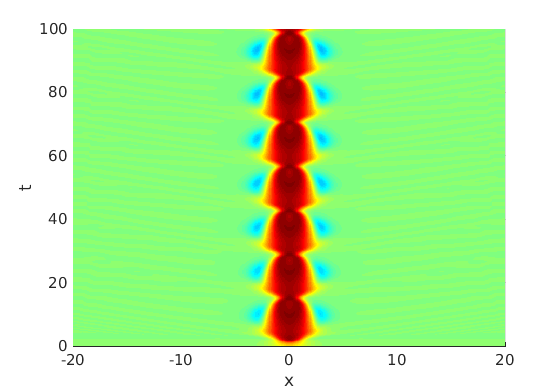
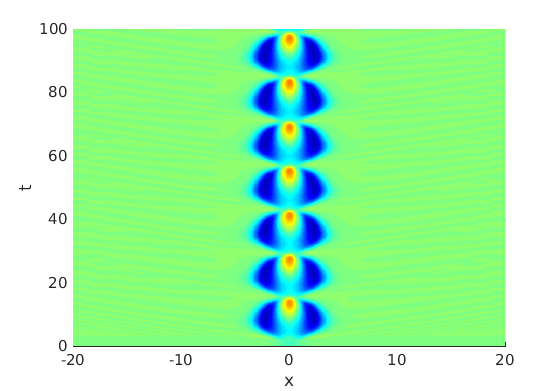
2.3 Numerical approximation of oscillating waves via freezing method
2.4 Spectra and eigenfunctions of oscillating waves
2.4.1 Point spectrum of oscillating waves on the imaginary axis
2.4.2 Essential spectrum of localized oscillating waves
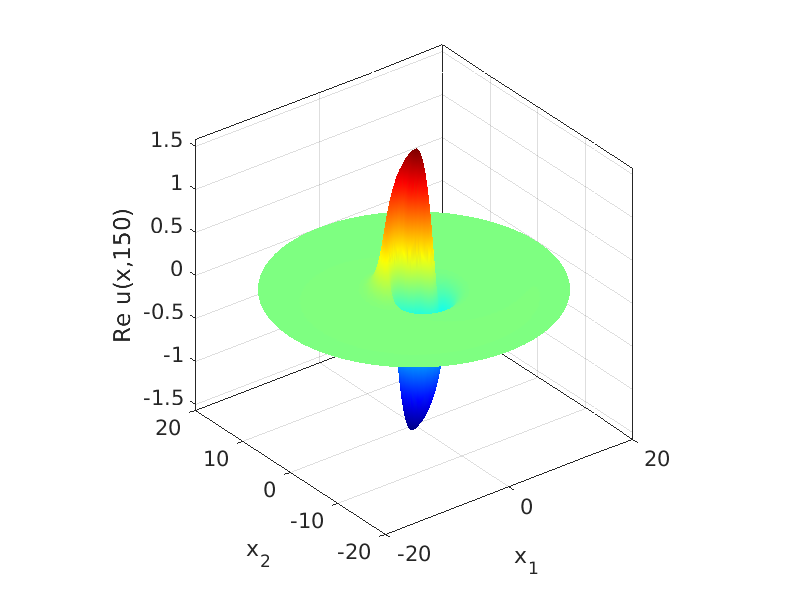
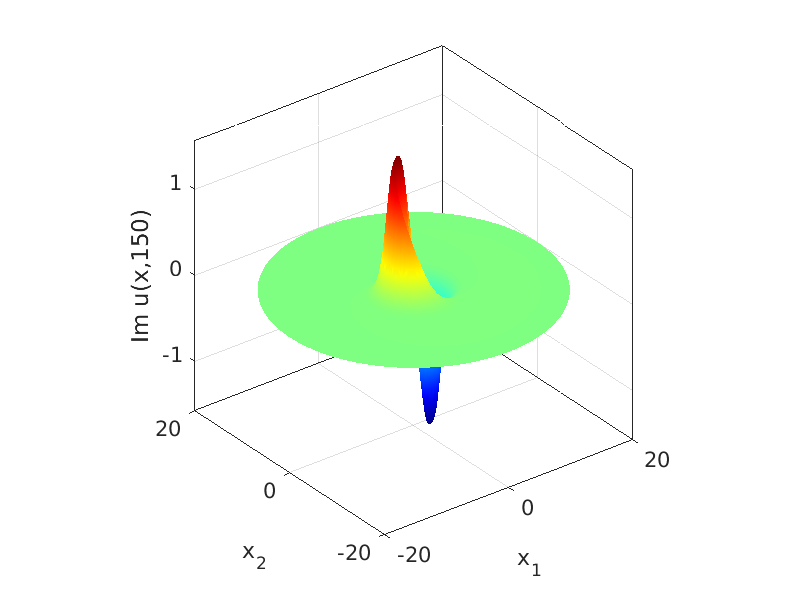
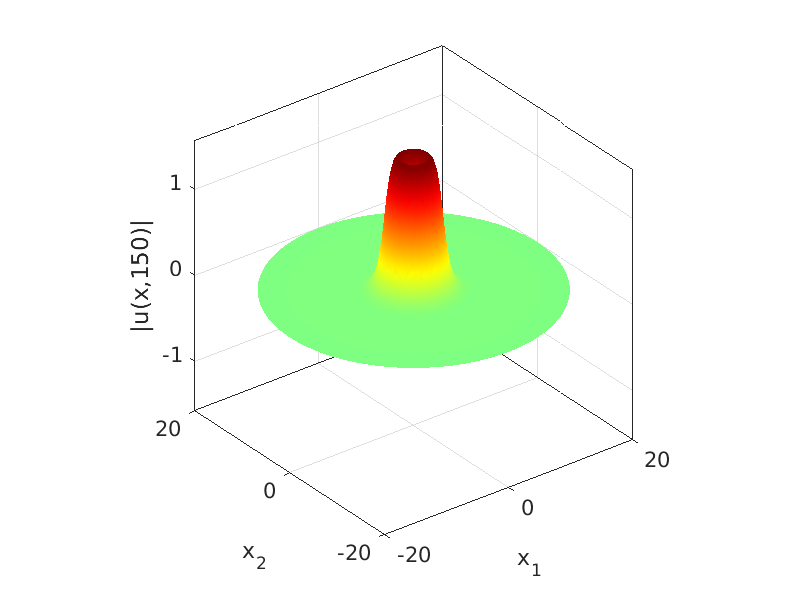
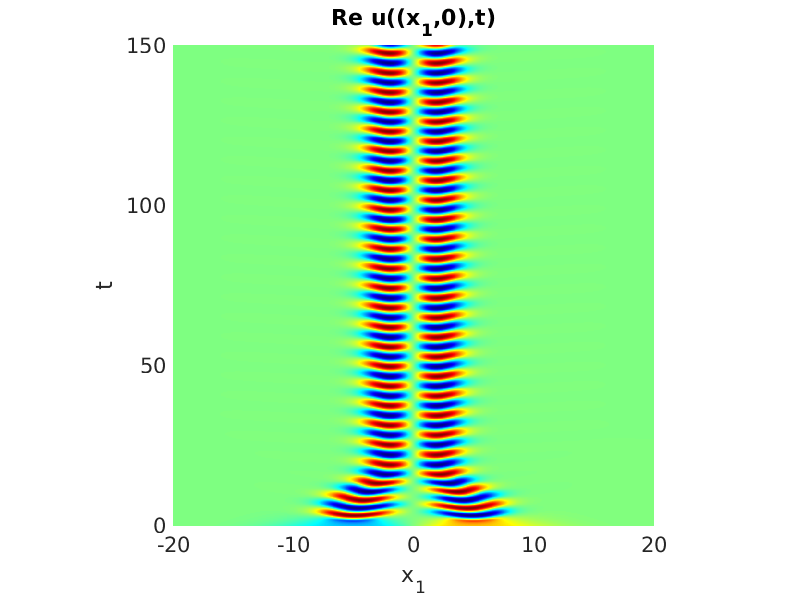
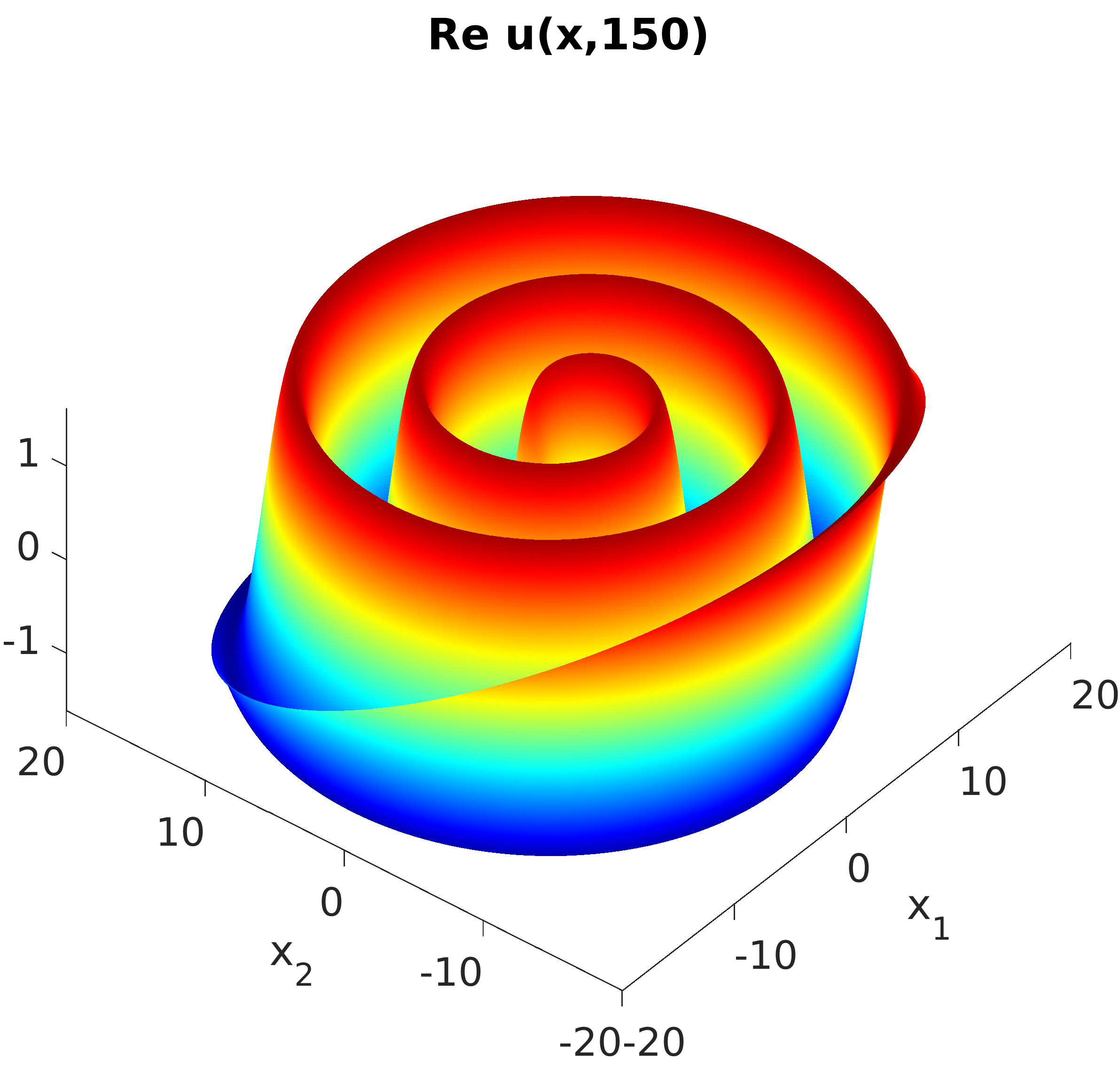
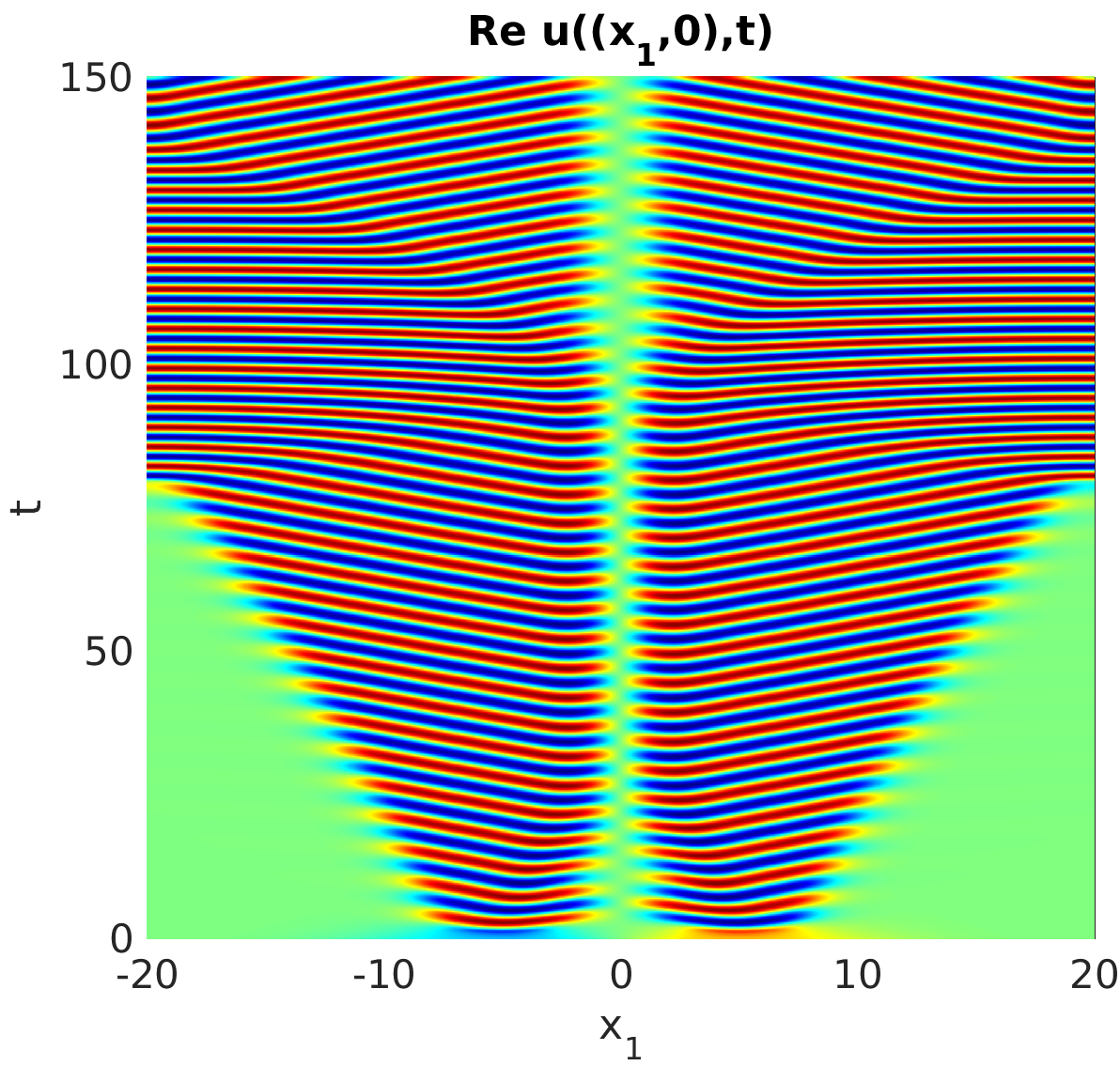
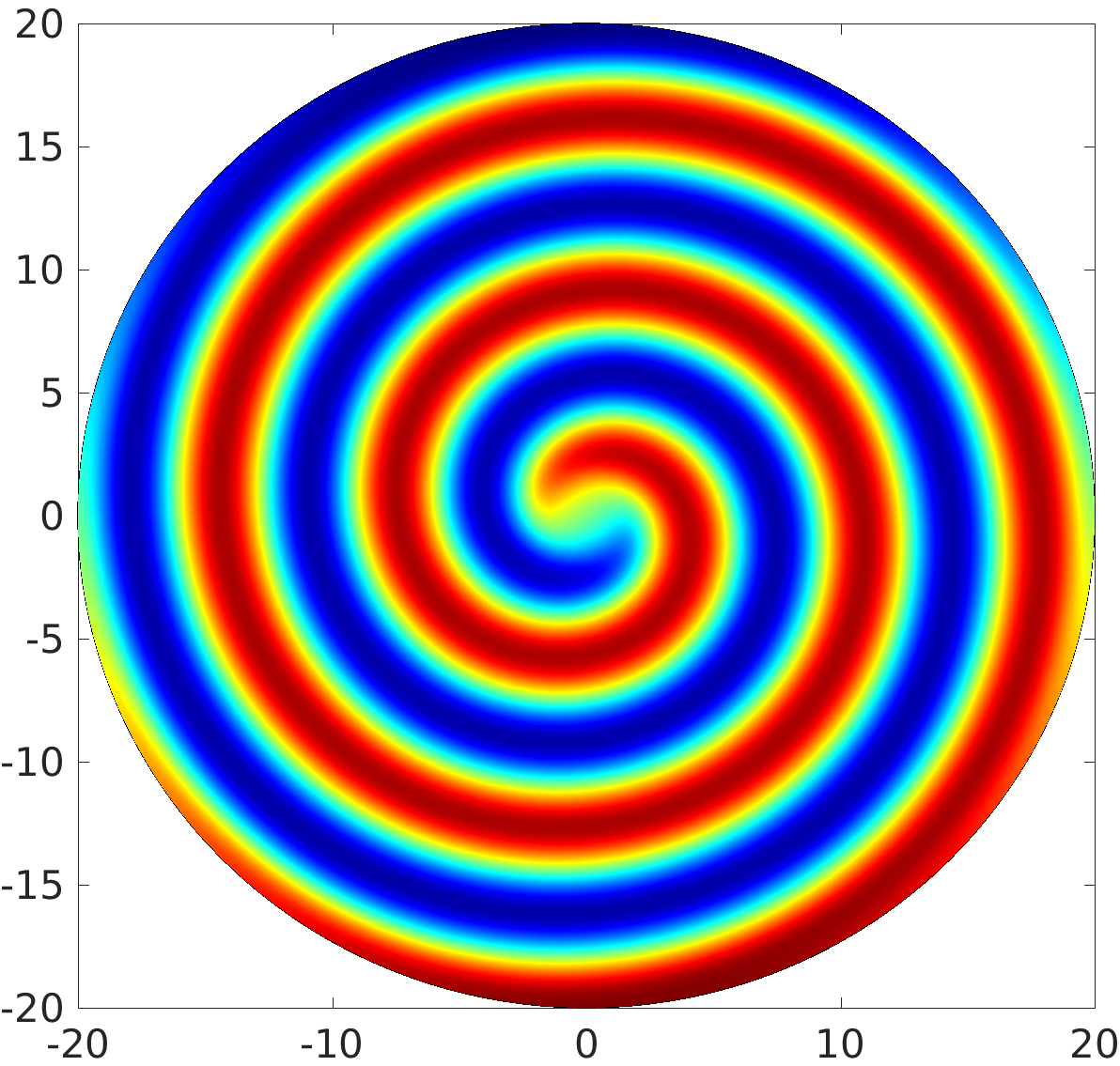
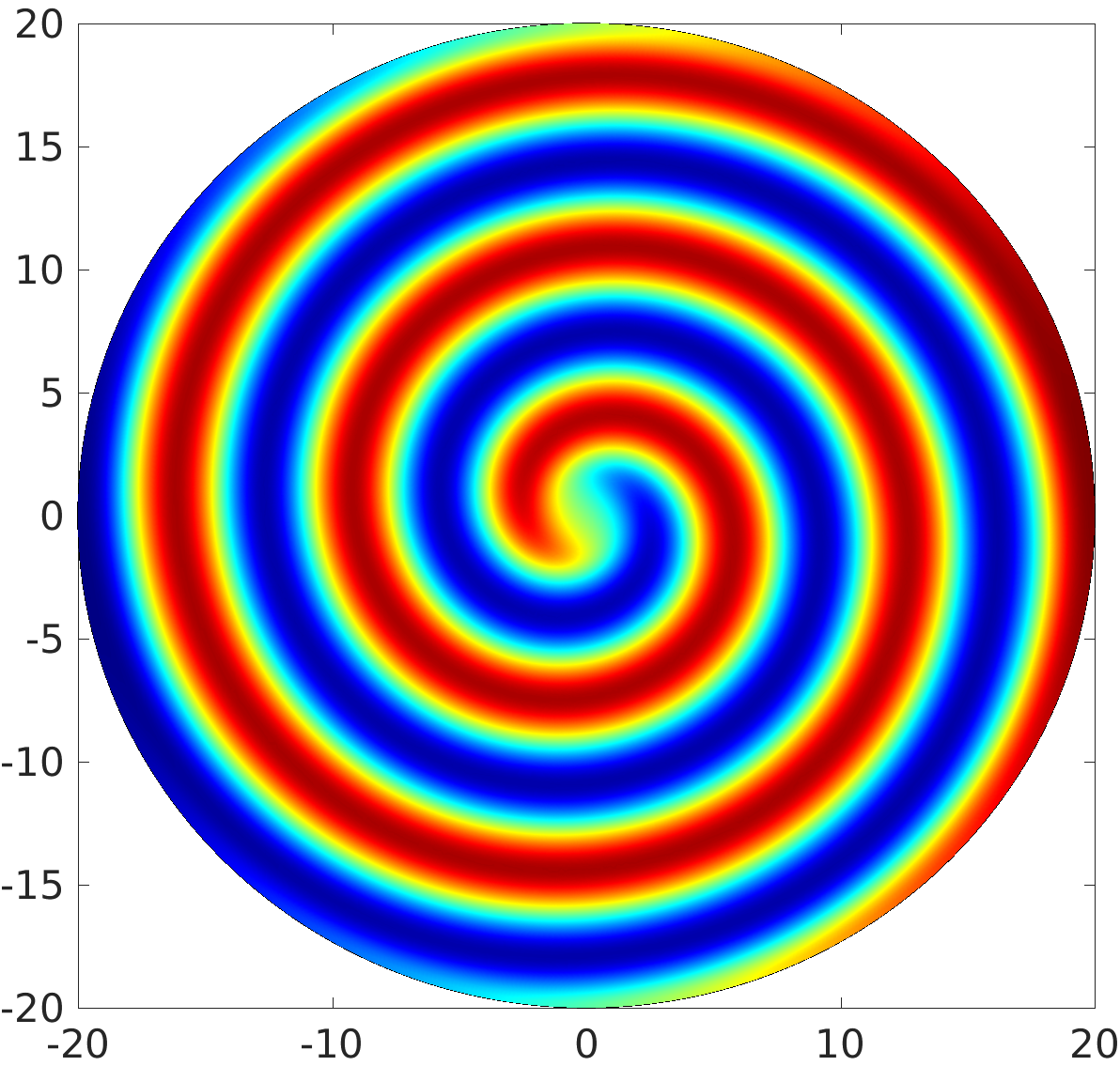
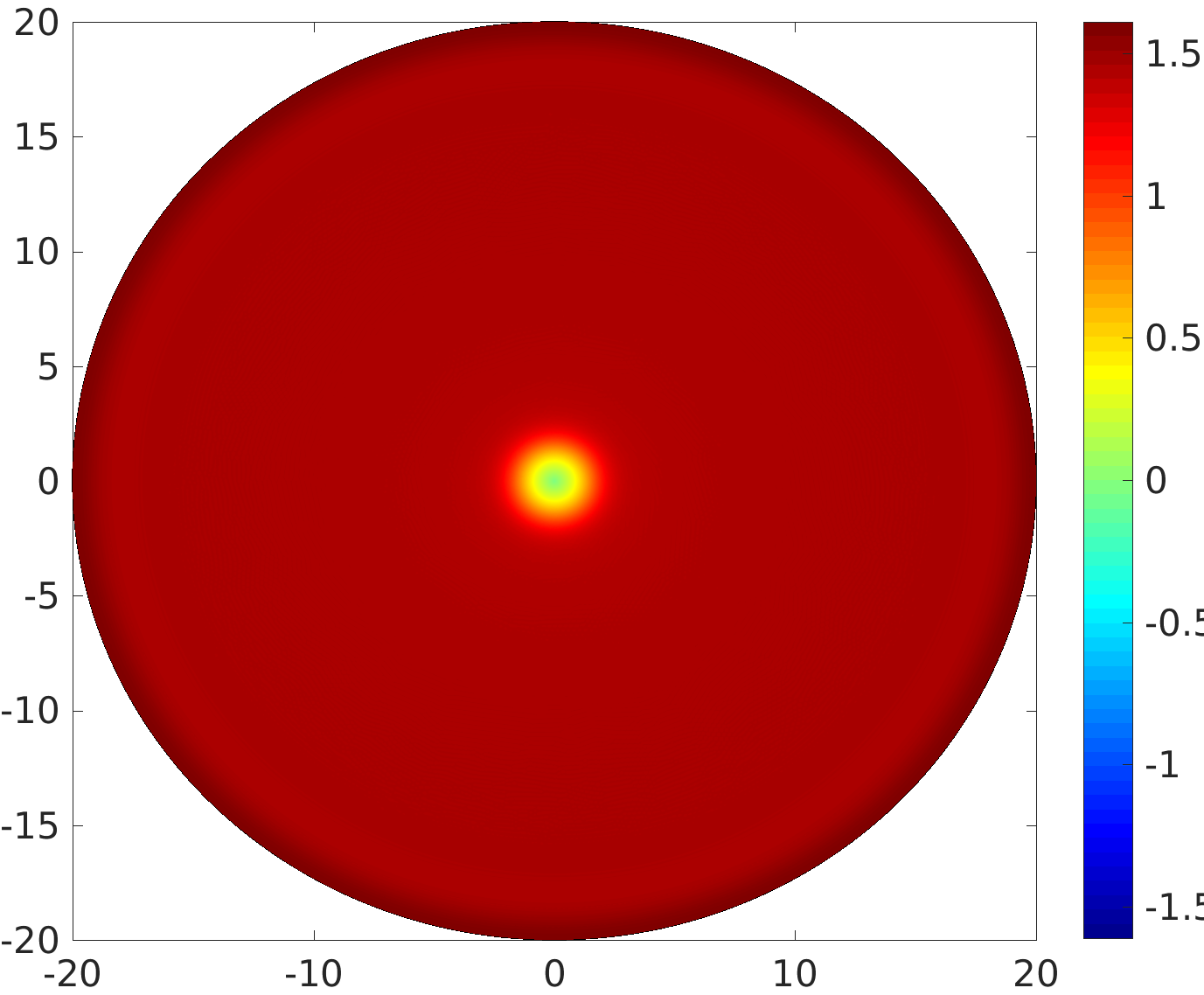
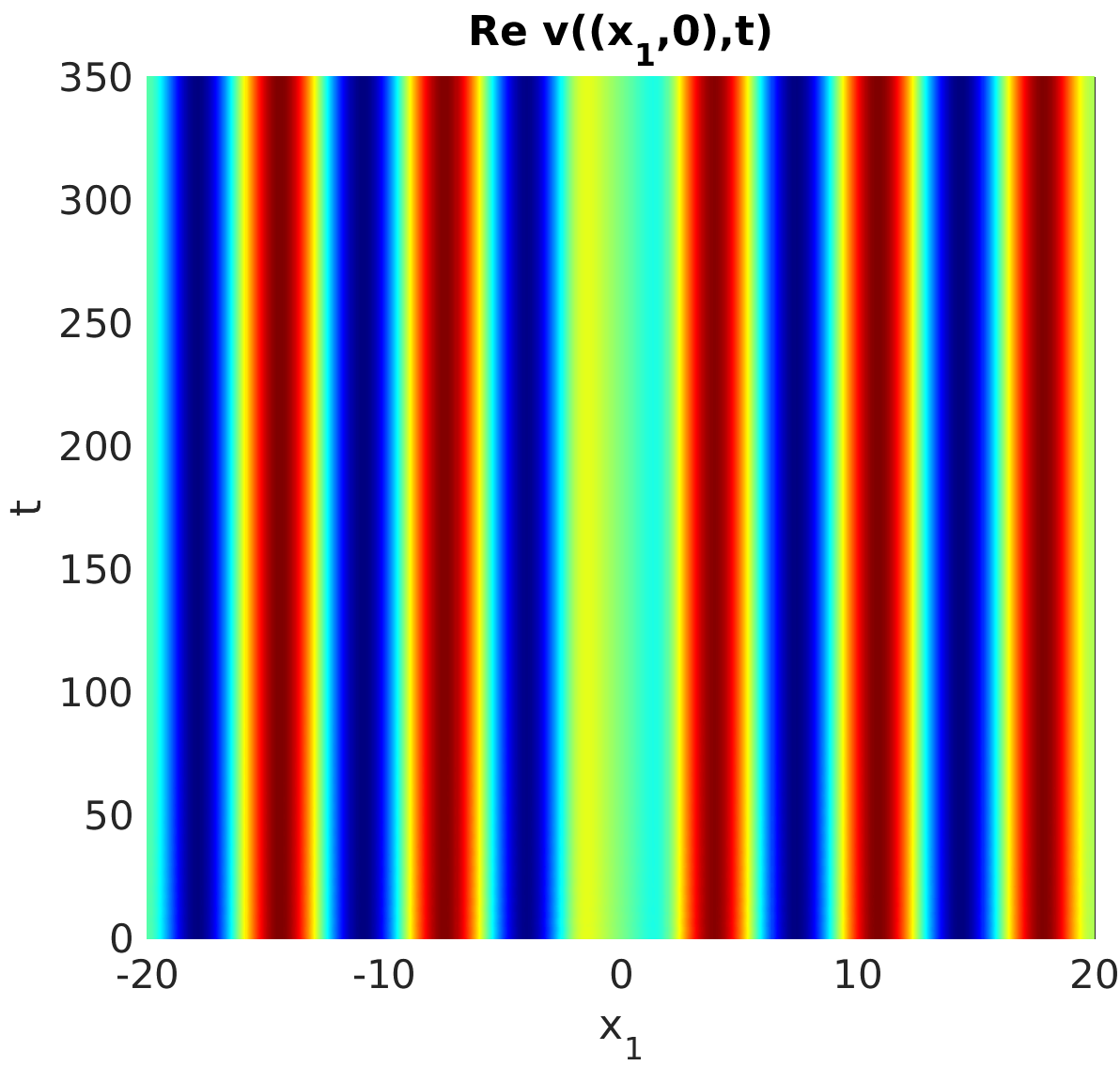
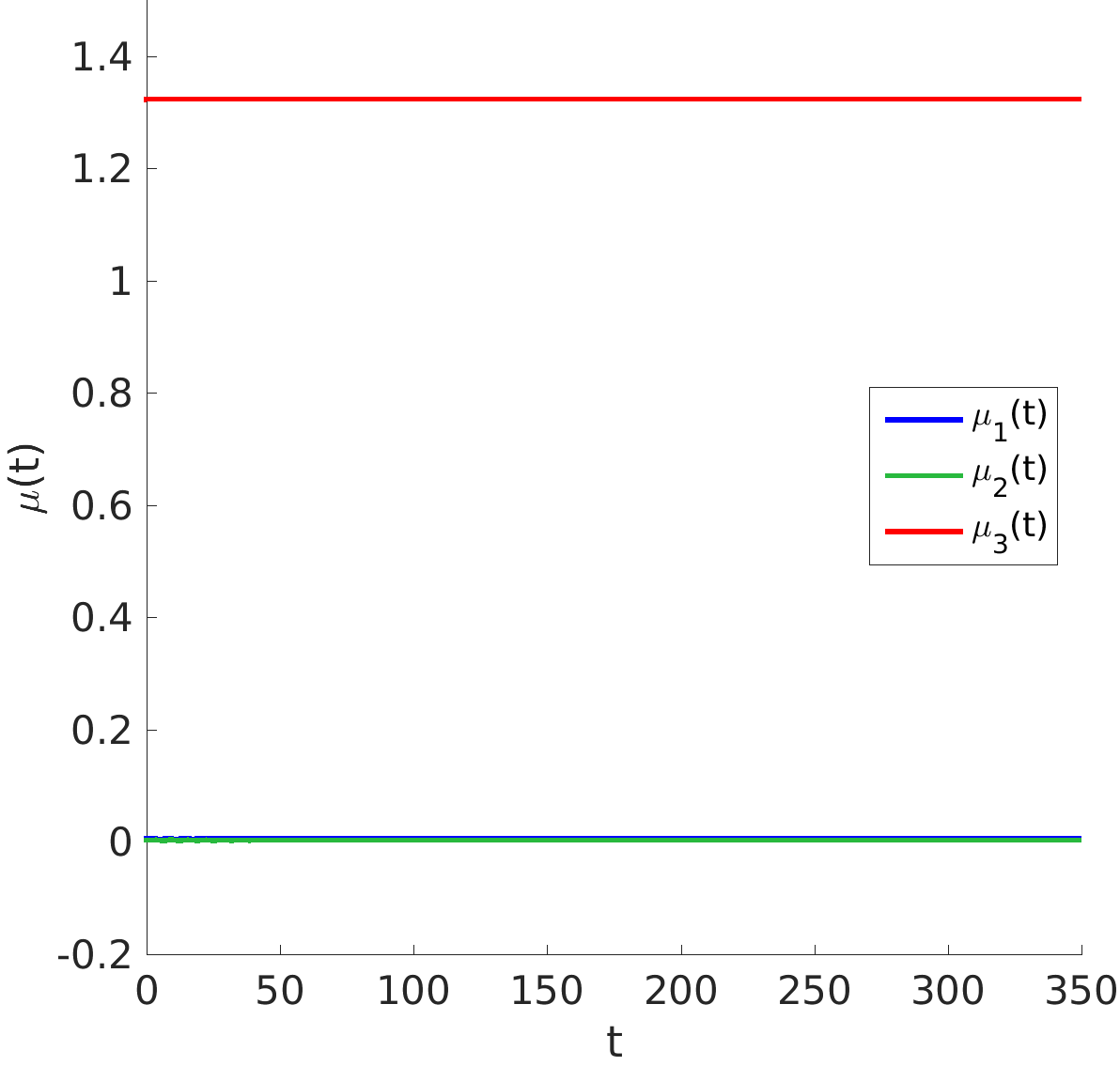
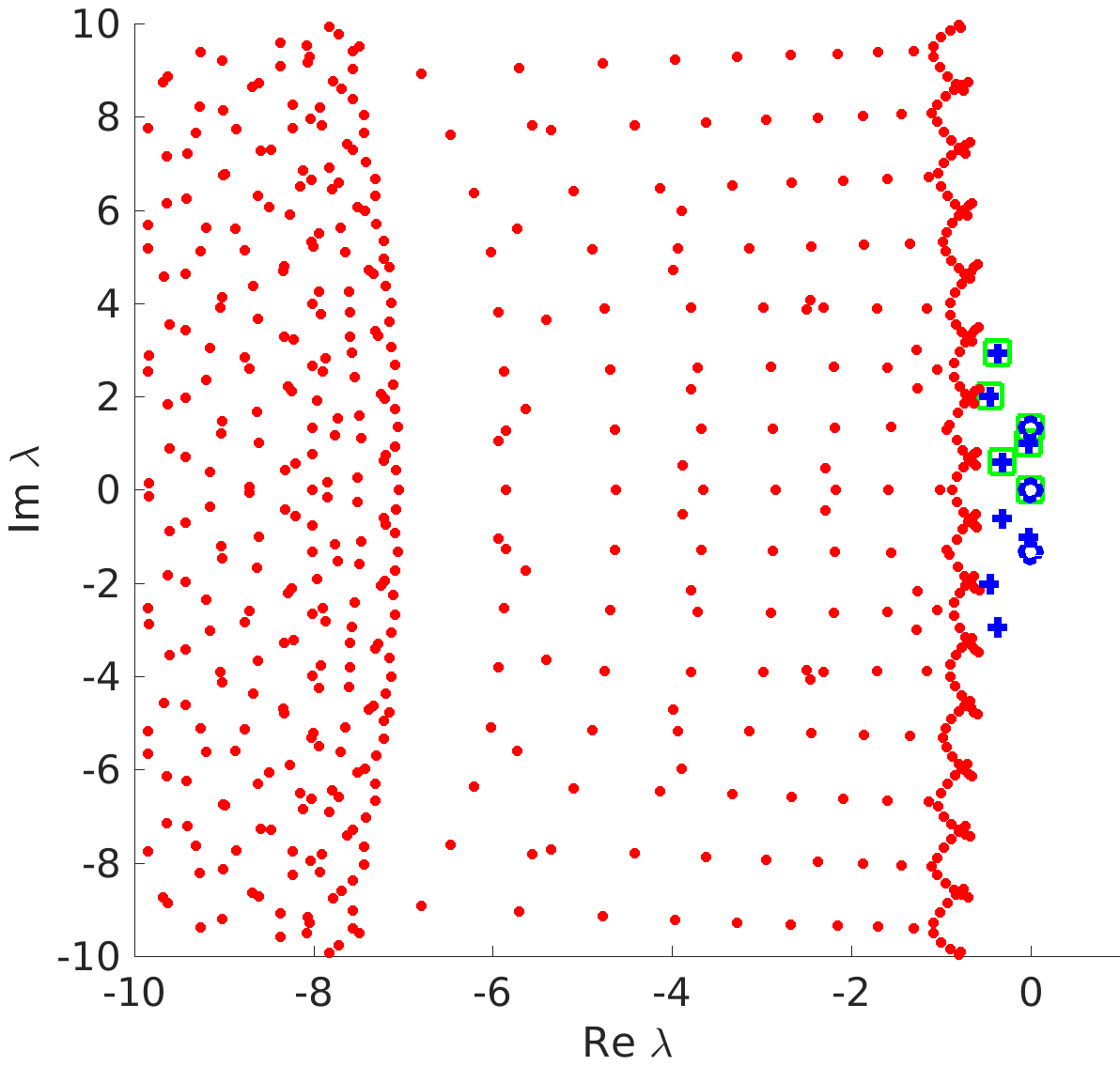
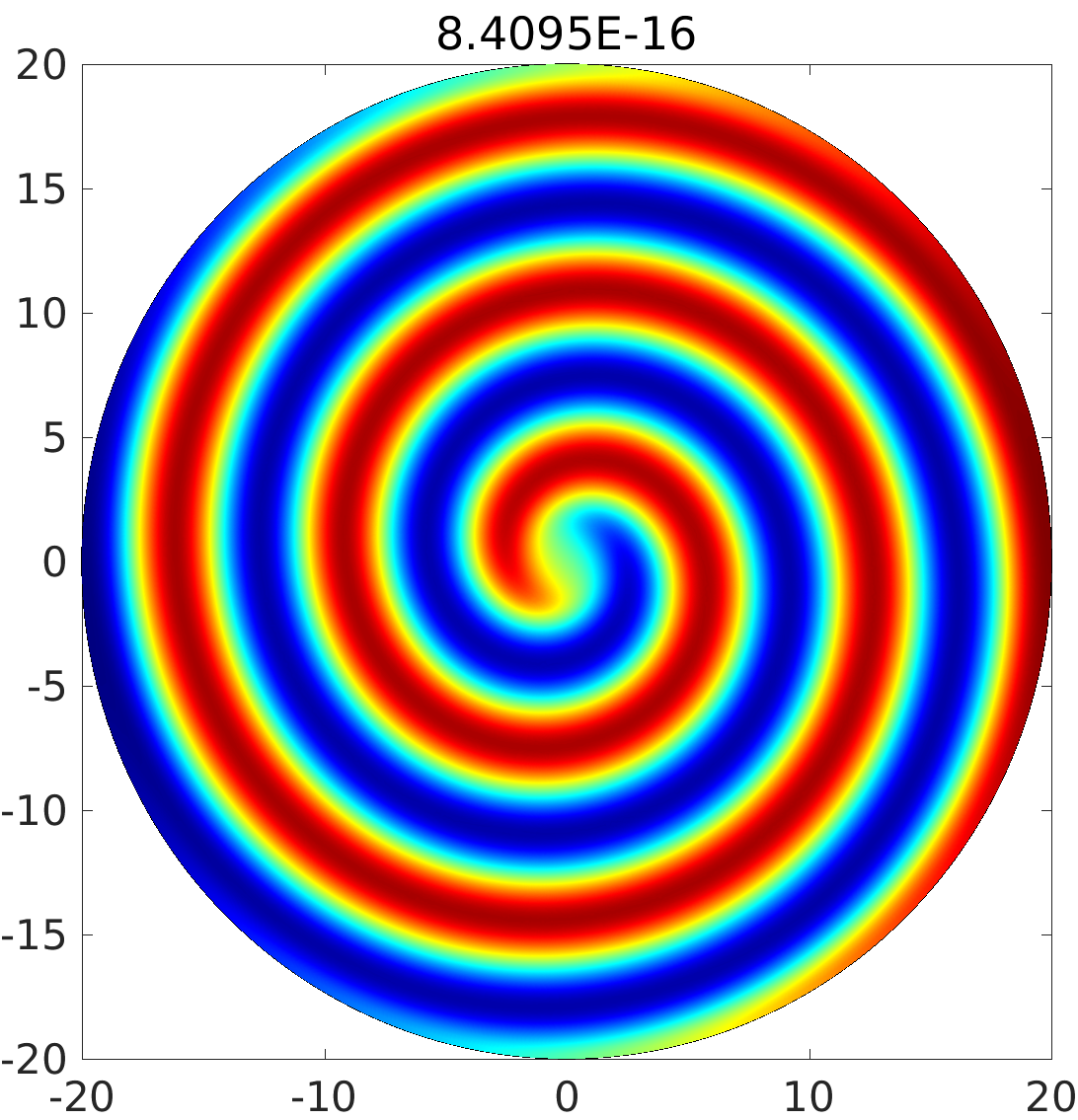
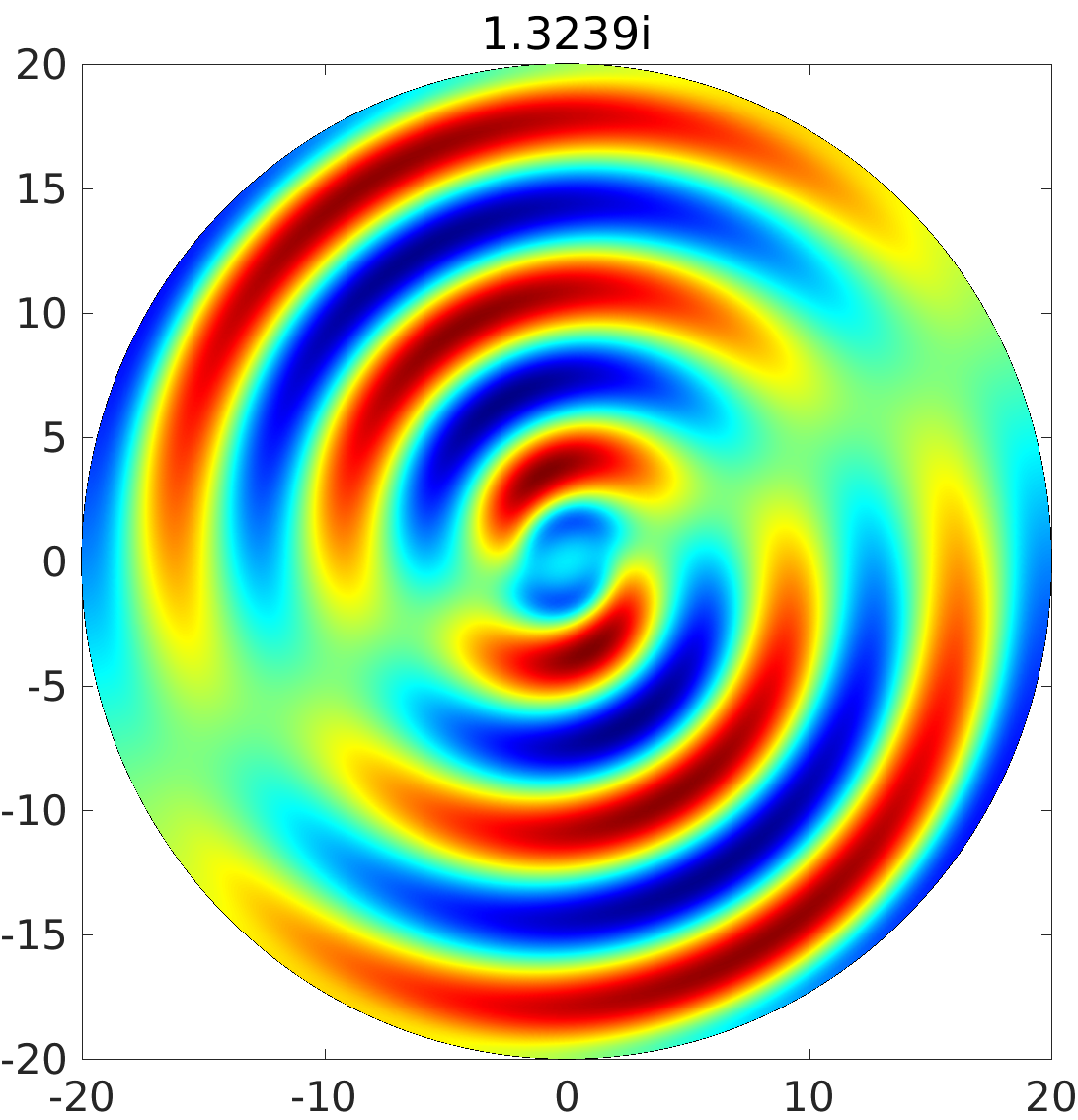
3.1 Rotating waves in reaction diffusion systems
3.2 Freezing method for rotating waves
3.3 Numerical approximation of rotating waves via freezing method
4. Freezing Waves with Several Symmetries in Reaction Diffusion Systems
5. Freezing Multistructures (Multifronts, Multipulses and Multisolitons) and Wave Interactions in Reaction Diffusion Systems
6. Further coherent structures in Reaction Diffusion Systems
Freezing Relative Equilibria in Equivariant Second-Order Evolution Equations (with Comsol Multiphysics 5.2)7.1 Traveling waves in systems of damped wave equations
7.2 Freezing method for traveling waves
7.3 Numerical approximation of traveling waves via freezing method
7.4 Spectra and eigenfunctions of traveling waves
7.4.1 Point spectrum of traveling waves on the imaginary axis
7.4.2 Essential spectrum of traveling waves
8. Freezing Rotating Waves in Damped Wave Equations
8.1 Rotating waves in systems of damped wave equations
8.2 Freezing method for rotating waves
8.3 Numerical approximation of rotating waves via freezing method
The model library of the examples below is summerized in the following file For the implementation of the results below we suggest the following Comsol tutorial Some further tutorials created by the older version Comsol 3.5a can be found here. Freezing Relative Equilibria in Equivariant First-Order Evolution Equations (with Comsol Multiphysics 5.1 and 5.2)1. Freezing Traveling Waves in Reaction Diffusion Equations
2. Freezing Oscillating Waves in Reaction Diffusion Equations
3. Freezing Rotating Waves in Reaction Diffusion Systems
4. Freezing Waves with Several Symmetries in Reaction Diffusion Systems
5. Freezing Multistructures (Multifronts, Multipulses and Multisolitons) and Wave Interactions in Reaction Diffusion Systems
6. Further coherent structures in Reaction Diffusion Systems
Freezing Relative Equilibria in Equivariant Second-Order Evolution Equations (with Comsol Multiphysics 5.1 and 5.2)7. Freezing Traveling Waves in Damped Wave Equations
8. Freezing Rotating Waves in Damped Wave Equations
Literature |